Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

:

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Опубликован: 27.05.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Уральский государственный экономический университет
Лекция 3:

Межотраслевой баланс
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234 || Лекция 4 >

3.2. Нахождение матрицы межотраслевых поставок и валовой продукции по матрице прямых затрат и вектору конечной продукции

Одна из основных задач межотраслевого баланса - найти при заданной структурной матрице А экономической системы в условиях баланса совокупный выпуск X, необходимый для удовлетворения заданного спроса Y.

Задача 3.1.

Рассмотрим - 3 сектора экономики ( промышленность, сельское хозяйство и транспорт).. В таблице приведены коэффициенты прямых затрат a_{ij} отчетного межотраслевого баланса и конечной продукции Y (цифры условные).

Производящие отрасли промышленность Сельское хозяйство Транспорт Конечная продукция Y
Потребляющие отрасли Коэфф. прямых затрат
промышленность 0,1 0,05 0,2 155
Сельское хозяйство 0,3 0,00 0,15 25
Транспорт 0,2 0,4 0,00 20
Чистая продукция V

Найти:

  1. Матрицу межотраслевых поставок.
  2. Матрицу полных затрат
  3. Для каждой отрасли объем валовой продукции
  4. Определить объемы чистой продукции
  5. Выполнить проверку проведенных вычислений, заполнить матрицу МОБ.

Запишем необходимые уравнения:

  • Матрица полных затрат B = (E - A)-1, Е - единичная матрица
  • Вектор валовой продукции X = B\times Y
  • Межотраслевые поставки x_{ij}= а_{ij}\times X_j
  • Выполняем проверку проведенных вычислений. В таблице МОБ рассчитываем :
  • Столбец Валовая продукция X_i = сумме по столбцам таблицы МОБ и конечного продукта X_i=\sum_{j=1}^{n}x_{ij}+Y_i, \;i=1,2..n
  • Строка условно чистая продукция V_j=X_j-\sum_{j=1}^{n}x_{ij} ( сумма по строкам)
  • Строка Валовая продукция – X_j=(X_i)^T
  • Суммарный конечный продукт равен суммарной условно чистой продукции \sum_{i=1}^{n}Y_i=\sum_{j=1}^{n}V_j

Решение

Для расчета в Mathcad используем операции с матрицами и с индексными переменными .

Входные данные. Расчет валовой продукции.

Матрица прямых затрат: A=\begin{pmatrix} 0.1 & 0.05 & 0.2 \\ 0.3 & 0 & 0.15 \\ 0.2 & 0.4 & 0 \end{pmatrix}

Вектор конечной продукции: Y=\begin{pmatrix} 155 \\ 25 \\ 20 \end{pmatrix}

Решение:

ORIGIN:=1

Вводим единичную матрицу identity(3)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

E:=identity(3)

Матрица полных затрат B:=(E-A)^{-1}, identity(3)=\begin{pmatrix} 1.228 & 0.17 & 0.217 \\ 0.431 & 1.123 & 0.255 \\ 0.418 & 0.483 & 1.156 \end{pmatrix}

Вектор объемов валовой продукции: X:=B\cdot Y, X=\begin{pmatrix} 200\\ 100\\ 100\end{pmatrix}

Расчет матрицы межотраслевых поставок

  • Расчет через индексные переменные

    i:=1..3,\; j:=1..3

    x_{i,j}:=A_{i,j}\cdot X_j

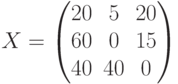    X=\begin{pmatrix} 20 & 5 & 20 \\ 60 & 0 & 15 \\ 40 & 40 & 0 \end{pmatrix} - матрица межотраслевых поставок

  • Расчет через матрицы

    С помощью функции diag построим диагональную квадратную матрицу, элементы главной диагонали которой являются элементами полученного вектора продукции X.

    X1:=diag(X), X1=\begin{pmatrix} 200 & 0 & 0 \\ 6 & 100 & 0 \\ 0 & 0 & 100 \end{pmatrix}

    x1:=A\cdot X1

    x1=\begin{pmatrix} 20 & 5 & 20 \\ 60 & 0 & 15 \\ 40 & 40 & 0 \end{pmatrix} - матрица межотраслевых поставок

Проверка проведенных вычислений. Расчет баланса в таблице МОБ.

Сумма по строкам (потребление отраслей):

\sum_{i=1}^{3}x_{i,j}

\begin{array}{|c|} \hline 120 \\ \hline 45 \\ \hline 35 \\ \hline \end{array}

Сумма по столбцам (производящие отрасли):

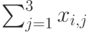
\sum_{j=1}^{3}x_{i,j}

\begin{array}{|c|} \hline 45 \\ \hline 75 \\ \hline 80 \\ \hline \end{array}

Вектор чистой продукции (Добавленная стоимость): V_j:=X_j-\sum_{i=1}^{3}x_{i,j}, V^T=(80\;55\;65)

Вектор валовой продукции:

Y_j+\sum_{j=1}^{3}x_{i,j}

\begin{array}{|c|} \hline 200 \\ \hline 100 \\ \hline 100 \\ \hline \end{array}

Дальше >>
< Лекция 2 || Лекция 3: 1234 || Лекция 4 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 29
Василий Долгополов
Василий Долгополов
Россия, Санкт-Петербург, БГТУ
предложить дружбу
Дмитрий Горский
Дмитрий Горский
Россия, Ростов-на-Дону, РГЭУ РИНХ, 2006
предложить дружбу