Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

:

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Опубликован: 27.05.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Уральский государственный экономический университет
Лекция 3:

Межотраслевой баланс
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234 || Лекция 4 >

3.4. Составление межотраслевого баланса затрат труда

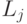Рассмотрим задачу межотраслевого баланса затрат труда и использования трудовых ресурсов. Предполагается, что труд выражается в единицах труда одинаковой степени сложности. Обозначим затраты живого труда в производстве j-го продукта через L_j, объем выпущенной продукции, как и прежде, X_j. Тогда коэффициент прямых затрат труда на единицу j-го продукта составят:

t_j=\frac{L_j}{X_j} ( 3.9)

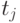t_j - прямые затраты труда на единицу j-го продукта;

Полные затраты труда представляют сумму прямых затрат (живого труда) и затрат овеществленного труда, перенесенных на продукт через израсходованные средства производства. Пусть 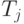T_j - полные затраты труда на единицу j-го продукта; a_{ij}T_i - затраты овеществленного труда, перенесенного на j-й продукт через i-е средство производства; тогда

T_j=\sum_{i=1}^{n}a_{ij}\cdot T_i+t_j, \;j=1..n ( 3.10)

Система (3.10) включает п уравнений по всем отраслям-потребителям. Если заданы матрица коэффициентов прямых материальных затрат и вектор-строка коэффициентов прямой трудоемкости, то решение системы (3.10) дает коэффициенты полных затрат труда на единицу каждого вида продукции. Перепишем (3.10) в матричном виде:

T=T\cdot A+t ( 3.11)

отсюда, выполняя простые матричные преобразования, получим:

T=t\cdot (E-A)^{-1} ( 3.12)

Поскольку 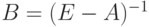B=(E-A)^{-1} матрица полных затрат, получаем формулу расчета матрицы коэффициентов полных затрат труда:

T=t\cdot B ( 3.13)

где T=(T_1,T_2,..,T_n) - вектор-строка коэффициентов полных затрат труда;

t_j = (t_1, t_2, ..., t_n) - вектор-строка коэффициентов прямых затрат труда.

Умножим обе части уравнения (3.13) на Y: T\cdot Y= t\cdot B\cdot Y, поскольку B\cdot Y=X (см. уравнение 3.8),

T\cdot Y=t\cdot X ( 3.14)

Уравнение (3.14) - баланс общих затрат труда: затраты в производстве = t\cdot X, получен конечный продукт : T\cdot Y.

Задача 3 .3.

Рассмотрим задачу с 3 секторами экономики (промышленность, сельское хозяйство и транспорт). В таблице приведены коэффициенты прямых затрат отчетного межотраслевого баланса, объемы конечной продукции в млн.руб. и затраты живого труда. Составить межотраслевой баланс затрат труда.

Производящие отрасли промышленность Сельское хозяйство Транспорт Конечная продукция
Потребляющие отрасли Коэффициенты прямых затрат
Промышленность 0,2 0,3 0,2 160
Сельское хозяйство 0,4 0,1 0,3 443
Транспорт 0,3 0,5 0,1 466
Затраты живого труда Lj 910 719 637

Решение.

Для составления межотраслевого баланса затрат труда необходимо найти следующие показатели

  1. Матрицу коэффициентов полных затрат .B
  2. Вектор валовой продукции X
  3. Матрицу межотраслевых поставок x_{ij}
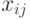
  4. Коэффициенты прямой трудоемкости 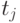t_j, Коэффициенты полной трудоемкости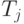 T_j
  5. Межотраслевые затраты труда xтр_{ij}
  6. Затраты труда на конечную продукцию Y\cdot t
  7. Заполнить матрицу МОБ. Выполнить проверку проведенных вычислений
  8. уравнения
  • Пункты 1-3 решены во 2 задаче.
  • Коэффициенты прямой трудоемкости t_j=L_j/X_j
  • Коэффициенты полных затрат труда: T = t\cdot B
  • Межотраслевые затраты труда xt_{ij}=x_{ij}\cdot t_i
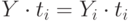
  • Затраты труда на конечную продукцию Y\cdot t_i=Y_i \cdot t_i

Выполняем проверку проведенных вычислений. В таблице МОБ рассчитываем баланс:

  • Сумма межотраслевых затрат труда и затрат труда на конечную продукцию равна затратам живого труда: \sum_{j=1}^{n}xt_{ij}+Yt_i \cdot L_i, \;i=1..n
  • Рассчитываем баланс затрат труда : затраты в производстве и получен конечный продукт : t\cdot X = T\cdot Y

Входные данные

Матрица прямых затрат: A:=\begin{pmatrix} 0.2& 0.3 & 0.2\\ 0.4 & 0.1 & 0.3\\ 0.3 & 0.5& 0.1 \end{pmatrix}

Вектор конечной продукции: Y:=\begin{pmatrix} 160 \\ 443 \\ 466 \end{pmatrix}

Затраты живого труда: L:=(910\; 719 \; 637), L^T:=\begin{pmatrix} 910\\ 719\\ 637\end{pmatrix}

Решение:

ORIGIN:=1

Вводим единичную матрицу: identity(3)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

E:=identity(3)

Матрица полных затрат: B:=(E-A)^{-1}, B:=\begin{pmatrix} 2.21& 1.24 & 0.9\\ 1.51 & 2.21 & 1.07\\ 1.57 & 1.64& 2.01 \end{pmatrix}

Вектор объемов валовой продукции: X:=B\cdot Y, X:=\begin{pmatrix} 1322\\ 1717\\ 1913\end{pmatrix}

Матрица межотраслевых поставок: i:=1..3, \; j:=1..3

x_{i,j}=A_{i,j}\cdot X_j, x:=\begin{pmatrix} 264& 515 & 383\\ 529 & 172 & 574\\ 397 & 859& 191 \end{pmatrix}

Коэффициенты прямой трудоемкости: t_i:=\frac{(L^T)_i}{X_i}, t:=\begin{pmatrix} 0.688\\ 0.419\\ 0.333\end{pmatrix}, t^T:=\begin{pmatrix} 0.688 & 0.419 & 0.333 \end{pmatrix}

Затраты живого труда на конечную продукцию: Yt_i:=Y_i \cdot t_i, Y_t:=\begin{pmatrix} 110.122\\ 185.466\\ 155.203\end{pmatrix}

Межотраслевые затраты труда: xt_{i,j}:=x_{i,j}\cdot t_i, xt=\begin{pmatrix} 182 & 355 & 263 \\ 221 & 72 & 240 \\ 132 & 286 & 64 \end{pmatrix}

Рассчитываем баланс. Сумма межотраслевых затрат труда и затрат труда на конечную продукцию равна затратам живого труда L

\sum_{j=1}^{3}xt_{i,j}=\sum_{j=1}^{3}xt_{i,j}+Yt_i

\begin{array}{|c|} \hline 799.878 \\ \hline 533.534\\ \hline 481.797\\ \hline \end{array}, \begin{array}{|c|} \hline 910 \\ \hline 719\\ \hline 637\\ \hline \end{array}, L^T=\begin{pmatrix} 910 \\ 719 \\ 637 \end{pmatrix}

t\cdot X=2.266\times 10^3 - затраты труда в производстве

T\cdot Y=2.266\times 10^3 - полные затраты труда при получении конечного продукта

Основные итоги

Приведены основные параметры и уравнения МОБ. Показано, как построить модель задачи МОБ, как выделить блок данных и блок решения. Продемонстрированы методы работы с матрицами и матричными уравнениями.

Ключевые термины

Межотраслевой баланс - инструмент анализа и прогнозирования структурных взаимосвязей в экономике.

Валовый продукт отрасли - суммарный объем продукции, потребляемой n отраслями, и конечного продукта.

Конечный продукт - объем продукции отрасли, предназначенный к потреблению в непроизводственной сфере (объём конечного потребления).

Матрица межотраслевых поставок -x{j} - матрица элементов, каждый определяет, сколько продукции i-й отрасли было использовано в процессе материального производства j-й отрасли.

Коэффициент прямых затрат - количество продукции i-ой отрасли, которое расходуется при производстве одной единицы продукции j-ой отрасли.

Коэффициент полных затрат - объем продукции i-й отрасли, расходуемый на производство единицы конечной продукции j-й отрасли,

Коэффициент полных затрат труда - затраты живого и овеществленного труда на производство единицы конечной продукции,

Коэффициент прямых затрат труда - затраты живого труда на производство единицы общего объема произведенной продукции.

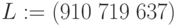Дальше >>
< Лекция 2 || Лекция 3: 1234 || Лекция 4 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 29
Василий Долгополов
Василий Долгополов
Россия, Санкт-Петербург, БГТУ
предложить дружбу
Дмитрий Горский
Дмитрий Горский
Россия, Ростов-на-Дону, РГЭУ РИНХ, 2006
предложить дружбу