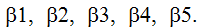Рисуем – развитие темы

Повторение при рисовании рисуем многоугольники, узоры

Рисуем: квадрат, треугольник, шестигранник

Практическое занятие в среде скретч "треугольник по направлениям"

Будем рисовать, используя вектора – то выбирать направление и идти по нему.

Открываем проект урока 7 "Рисуем". Рисовать мы будем карандашом.

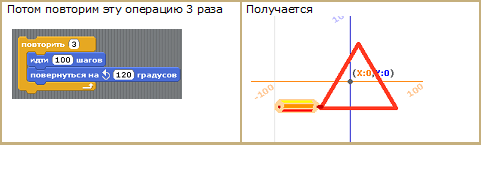
Например, мы можем нарисовать треугольник.

Сначала нарисуем одну сторону

Чем это лучше, чем рисовать по координатам?

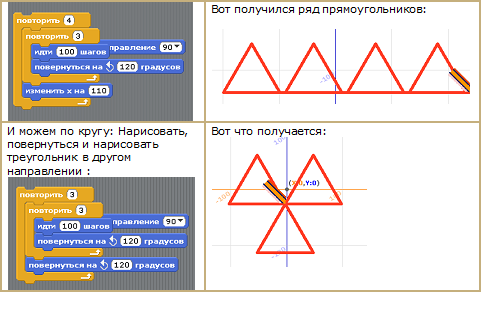
Мы можем нарисовать треугольник под углом.

Мы можем нарисовать треугольники в ряд

Нарисовать, потом передвинуться, потом опять нарисовать.

Сохраняем проект командой "Сохранить как" с именем "Рисуем треугольник".

Проект "Рисуем" нам еще пригодится.

Многоугольник

Теория

Многоугольник – это треугольники, четырехугольники, пятиугольники, …

Выделяются также четырехугольники, у которых все углы прямые (90 градусов) - это прямоугольники

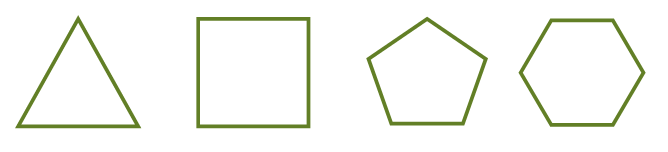
Правильные многоугольники – это многоугольники, у которых все стороны и все углы одинаковые. Примеры таких многоугольников ниже:

Вычисление углов правильного n-угольника

Угол правильного n-угольника: 180 * (n-2)/n.

Доказательство

На рисунке пример многоугольника — пятиугольник с углами

Возьмем муравья, который идет по сторонам многоугольника. По часовой стрелке и обходит все стороны последовательно. При этом он поворачивает последовательно на углы α ₁, α ₂, α ₃, α ₄, α ₅

Угол самого многоугольника — это угол 180° минус угол поворота робота вокруг этого угла.

Так как он поворачивает все время в одну сторону и потом возвращается к тому же направлению он описывает полный круг.

Значит сумма углов поворота — 360 градусов.

На нашем пятиугольнике сумма углов α ₁ + α ₂ + α ₃ + α ₄ + α ₅

Значит, сложив n углов, мы получим

180°* n — сумма-углов-поворота = 180°* n — 360 = 180°*(n - 2 )

Например, в пятиугольнике на рисунке

Сумма углов α ₁ + β ₁=180°

Так как все углы равны, α ₁ = α ₂=...=(180°*(n - 2 )/n