Память c иcпользованием СТП и спинтронные логические схемы

2. Логика на наномагнитах

К первому поколению спинтронных логических элементов следует отнести также т.н. "логику на наномагнитах" (англ. Nanomagnetic logic – NML), которую называют также "магнитные клеточные автоматы", (МКА, англ. Magnetic cellular automata, MCA). Для построения такой логики используют продолговатые ферромагнитные элементы (рис. 2.7.а), имеющие выраженную анизотропию формы. Поэтому в равновесии они могут находиться лишь в состоянии намагниченности вдоль длинной оси. Их делают из магнитомягких материалов, чаще всего из пермаллоя (Fe20Ni80) или из супермаллоя (Ni80Fe14Mo5X1, где X – другой металл). Оптимальными размерами считают приблизительно 20 х 60 х 120 нм, когда ферромагнитный наноэлемент (далее ФНЭ) представляет собой один единый домен, надежно сохраняет состояние намагниченности при комнатных температурах и имеет еще относительно небольшую энергию перемагничивания (порядка 60kТ, где k – постоянная Больцмана, Т – рабочая температура). В дальнейшем взаимное расположение таких элементов мы для простоты показываем в виде сверху.

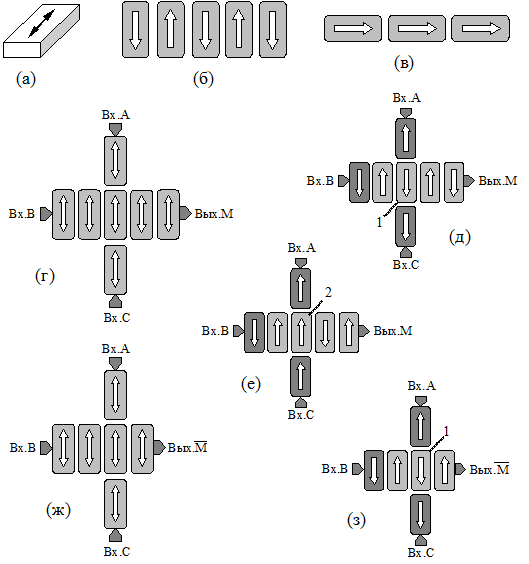
Рис. 2.7. (а) Типичная форма ферромагнитных элементов МКА. (б) Антиферромагнитное упорядочение. (в) Упорядочение при стыковке магнитными полюсами. (г) Мажоритарная логическая схема. (д, е) Примеры ее работы. (ж) Антимажоритарная схема. (з) Один из примеров ее работы

Если несколько ФНЭ разместить рядом длинными сторонами друг к другу ( рис. 2.7.б, типичное расстояние 15-30 нм), то устойчивое состояние (наименьшая потенциальная энергия) достигается тогда, когда направления намагниченности соседних ФНЭ противоположны. Поэтому строка расположенных таким образом ФНЭ автоматически приобретает антиферромагнитную намагниченность. Если же ФНЭ расположены рядом магнитными полюсами друг к другу ( рис. 2.7.в), то наименьшая потенциальная энергия достигается тогда, когда направления намагниченности соседних элементов совпадают.

Используя указанные свойства взаимодействия ФНЭ, можно построить их конфигурации, выполняющие те или иные логические функции. На рис. 2.7.г показана наиболее употребляемая конфигурация, выполняющая логическую функцию мажоритарного элемента Μ(A,B,C) На рис. 2.7.д показан один из примеров ее работы. Здесь входные ФНЭ внешними силами переведены в конкретные состояния намагниченности. Если считать намагниченность вверх логическим "0", а намагниченность вниз логической "1", то А = 0, В = С = 1. На ФНЭ, обозначенный цифрой 1, сверху действует сила, стремящаяся развернуть его намагниченность вверх, снизу – сила, стремящаяся развернуть его намагниченность вниз, и слева – сила, которая тоже стремится развернуть его намагниченность вниз. Суммарное действие двух последних сил побеждает, и намагниченность элемента 1 разворачивается вниз. Поэтому и выходной ФНЭ имеет намагниченность вниз, т.е. приходит в состояние логической "1". Т.е. на выходе имеем состояние, которое совпадает с состоянием большинства входных элементов.

На рис. 2.7.е показан еще один пример работы мажоритарного логического элемента. Здесь входные ФНЭ внешними силами переведены в состояния А = С = 0, В = 1. На ФНЭ, обозначенный цифрой 2, сверху и снизу действуют силы, стремящиеся развернуть его намагниченность вверх, а слева – сила, стремящаяся развернуть его намагниченность вниз. Суммарное действие первых двух сил побеждает, и намагниченность элемента 1 разворачивается вверх. Поэтому и выходной ФНЭ имеет намагниченность вверх, т.е. приходит в состояние логического "0".

Благодаря антиферромагнитному упорядочению горизонтальных строк логическая операция отрицания реализуется очень просто – добавлением или удалением одного ФНЭ в строке. На рис. 2.7.ж показана конфигурация, реализующая логическую функцию антимажоритарного элемента 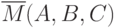. Один из конкретных примеров ее работы показан на рис. 2.7.з. Здесь А = 0, В = С = 1. На ФНЭ, обозначенный цифрой 1, сверху действует сила, которая стремится развернуть его намагниченность вверх, снизу – сила, стремящаяся развернуть его намагниченность вниз, и слева - сила, тоже стремящаяся развернуть его намагниченность вниз. Суммарное действие двух последних сил побеждает, и намагниченность элемента 1 разворачивается вниз. Поэтому выходной ФНЭ имеет намагниченность вверх, т.е. приходит в состояние логического "0".

Описанные мажоритарные логические схемы могут выполнять логические функции AND, OR, NAND, NOR, а именно: 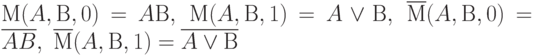. Они образуют функционально полный набор логических элементов, и поэтому с помощью сети МКА можно реализовать любые, даже довольно сложные процессоры.

Для того, чтобы формировать заданные состояния входных ФНЭ и считывать состояния выходных ФНЭ сети МКА, можно использовать, например, узлы записи и считывания ( рис. 2.2.б,в) такие же, как и в описанной выше трековой памяти.

С целью уменьшения энергопотребления при переключении ФНЭ из одного состояния в другое и ускорения этого переключения часто применяют магнитное поле, перпендикулярное к направлению намагниченности ФНЭ. В таком поле намагниченность ФНЭ принудительно разворачивается перпендикулярно к оси легкого намагничивания, т.е. приводится в нейтральное состояние, из которого ФНЭ может легко перейти в любое из стабильных состояний. Такое пульсирующее внешнее магнитное поле создается на короткое время непосредственно перед подачей новых входных данных и выключается при их поступлении. Оно как бы "стирает", нейтрализует все предыдущие состояния и значительно облегчает и ускоряет переход ФНЭ в новые состояния в соответствии с новыми входными данными.

Заметим еще, что нередко описанную сеть ФНЭ называют "магнитными клеточными автоматами на квантовых точках" ("magnetic quantum-dot cellular automata"), что является неточным. ФНЭ указанных размеров (≈ 20 х 60 х120 нм) не являются настоящими квантовыми точками в том плане, что их размеры еще значительно превышают длину волны де Бройля для носителей заряда. И о квантовых вычислениях здесь речь еще не идет.