Лексический анализ
Конечные автоматы
Регулярные выражения, введенные ранее, служат для описания регулярных множеств. Для распознавания регулярных множеств служат конечные автоматы. Недетерминированный конечный автомат (НКА) - по определению есть пятерка M = (Q, T, D, q0, F), где
- Q - конечное множество состояний,
- T - конечное множество допустимых входных символов (входной алфавит),
-
D - функция переходов (отображающая множество
 во множество подмножеств множества Q ),
определяющая поведение управляющего устройства,
во множество подмножеств множества Q ),
определяющая поведение управляющего устройства, -
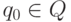 - начальное состояние управляющего
устройства,
- начальное состояние управляющего
устройства, -
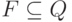 - множество заключительных состояний.
- множество заключительных состояний.
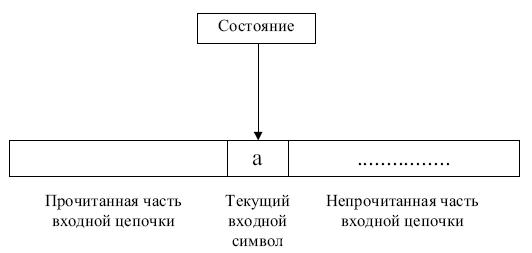
Работа конечного автомата представляет собой некоторую последовательность шагов, или тактов. Такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния и, возможно, сдвига входной головки на одну ячейку вправо ( рис. 3.2.).
Недетерминизм автомата заключается в том, что, во- первых, находясь в некотором состоянии и обозревая текущий символ, автомат может перейти в одно из, вообще говоря, нескольких возможных состояний, и во-вторых, автомат может делать переходы по e.
Пусть M = (Q, T, D, q0, F) - НКА. Конфигурацией
автомата M называется пара 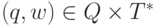 , где q -
текущее состояние управляющего устройства, а w - цепочка
символов на входной ленте, состоящая из символа под
головкой и всех символов справа от него. Конфигурация
( q0, w ) называется начальной, а конфигурация ( q, e ), где
, где q -
текущее состояние управляющего устройства, а w - цепочка
символов на входной ленте, состоящая из символа под
головкой и всех символов справа от него. Конфигурация
( q0, w ) называется начальной, а конфигурация ( q, e ), где  - заключительной (или допускающей). Тактом
автомата M называется бинарное отношение
- заключительной (или допускающей). Тактом
автомата M называется бинарное отношение 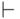 , определенное
на конфигурациях M следующим образом: если
, определенное
на конфигурациях M следующим образом: если  ,
где
,
где 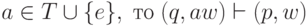 для всех
для всех  .
.
Будем обозначать символом  транзитивное (рефлексивно-транзитивное) замыкание отношения
транзитивное (рефлексивно-транзитивное) замыкание отношения 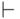 .
Будем говорить, что автомат M допускает цепочку w,
если
.
Будем говорить, что автомат M допускает цепочку w,
если  для некоторого
для некоторого  . Языком,
допускаемым, (распознаваемым, определяемым) автоматом M, (обозначается L(M) ), называется множество входных
цепочек, допускаемых автоматом M. То есть,
. Языком,
допускаемым, (распознаваемым, определяемым) автоматом M, (обозначается L(M) ), называется множество входных
цепочек, допускаемых автоматом M. То есть,

Важным частным случаем недетерминированного конечного автомата является детерминированный конечный автомат, который на каждом такте работы имеет возможность перейти не более чем в одно состояние и не может делать переходы по e.
Пусть M = (Q, T, D, q0, F) - НКА. Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия:
-
 , для любого
, для любого 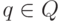 , и
, и -
D(q, a) содержит не более одного элемента для любых
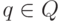 и
и  .
.
Так как функция переходов ДКА содержит не более одного элемента для любой пары аргументов, для ДКА мы будем пользоваться записью D(q, a)=p вместо D(q, a)={p}.
Конечный автомат может быть изображен графически
в виде диаграммы, представляющей собой ориентированный
граф, в котором каждому состоянию соответствует вершина,
а дуга, помеченная символом 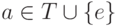 , соединяет две
вершины p и q, если
, соединяет две
вершины p и q, если  . На диаграмме выделяются
начальное и заключительные состояния (в примерах ниже,
соответственно, входящей стрелкой и двойным контуром).
. На диаграмме выделяются
начальное и заключительные состояния (в примерах ниже,
соответственно, входящей стрелкой и двойным контуром).
Пример 3.3. Пусть L = L(r), где r = (a|b)*a(a|b)(a|b).
-
- Недетерминированный конечный автомат M, допускающий
язык L:
M = {{1, 2, 3, 4}, {a, b}, D, 1, {4}},
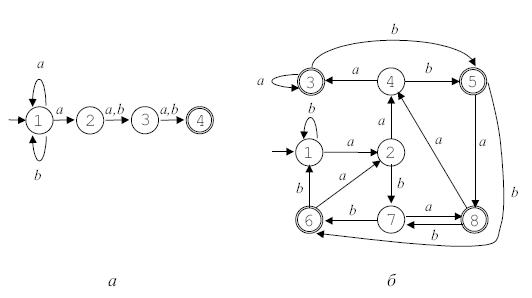
где функция переходов D определяется так:Диаграмма автомата приведена на рис. 3.3 а.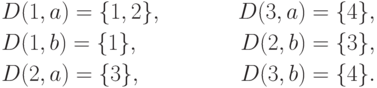
- Детерминированный конечный автомат M, допускающий
язык L:
M = {{1, 2, 3, 4, 5, 6, 7, 8}, {a, b}, D, 1, {3, 5, 6, 8}}
где функция переходов D определяется так:
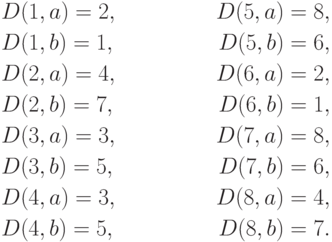
Диаграмма автомата приведена на рис. 3.3 б.
- Недетерминированный конечный автомат M, допускающий
язык L:
Пример 3.4. Диаграмма автомата, допускающего множество чисел в десятичной записи, приведена на рис. 3.4.
Пример 3.5. Анализ цепочек.
- При анализе цепочки w = ababa автомат из примера
рис.
3.3, а,
может сделать следующую последовательность тактов:Состояние 4 является заключительным, отсюда, цепочка w допускается этим автоматом.
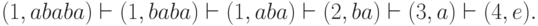
- При анализе цепочки w = ababab автомат из примера
рис.
3.3, б,
должен сделать следующую последовательность тактов:Так как состояние 7 не является заключительным, цепочка w не допускается этим автоматом.