Атрибутные грамматики

Теорема B.15. Задача определения того, является ли произвольная атрибутная грамматика чистой многопроходной слева-направо, зависит экспоненциально от размера атрибутной грамматики.

Пример B.4. Существуют атрибутные грамматики, вычисляющиеся в обоих направлениях, но не вычисляющиеся в одном ( рис. B.4).

Рис. B.4.

Атрибутная грамматика называется простой k - проходной в обоих направлениях, если существует такая последовательность обходов и такое разбиение атрибутов , каждого символа, что все атрибуты из множества Ai(X) вычисляются на i -ом проходе дерева [5].

Атрибутная грамматика называется простой многопроходной в обоих направлениях ( SBD ), если она является простой k -проходной в обоих направлениях для какого-нибудь k.

Грамматика примера 9.2 является простой многопроходной в обоих направлениях, но не является чистой многопроходной слева-направо. Грамматика примера 9.3 является чистой многопроходной слева-направо, но не является простой многопроходной в обоих направлениях. Так что между классами PLR и SBD нет отношения включения.

Теорема B.16. Задача проверки того, является ли произвольная атрибутная грамматика простой k - проходной в обоих направлениях, полиномиально сложна [5].

Пример B.5.Существуют грамматики, являющиеся чистыми многопроходными, но не являющиеся простыми многопроходными ( рис. B.5).

Рис. B.5.

Атрибутная грамматика называется простой k -проходной слева-направо, если существует такое разбиение атрибутов каждого символа что все атрибуты из множества Ai(X) вычисляются на i -ом обходе дерева слева-направо сверху-вниз.

Атрибутная грамматика называется простой многопроходной слева-направо ( SLR ), если она является простой k -проходной слева-направо для какого-нибудь k.

Пример B.6. Эта грамматика является простой однопроходной справа-налево, но не является простой однопроходной слева-направо ( рис. B.6).

Рис. B.6.

Будем говорить, что между атрибутами a и b имеет место отношение prec, если существует правило вывода p : X₀->X₁ ... X_np с вхождениями атрибутов a<j> и b<k> такое, что a<j> используется в качестве аргумента при вычислении вхождения b<k>.

Между атрибутами a и b имеет место отношение L, если aprecb и для каждого правила вывода p : X₀->X₁ ... X_np с вхождениями атрибутов a<j> и b<k> такими, что b<k> зависит от a<j>, имеет место j<k.

Графом LR -предшествования для AG назовем граф, вершинами которого являются атрибуты всех символов AG и из вершины a в вершину b идет дуга, тогда и только тогда, когда имеет место отношение aprecb. Если имеет место отношение aLb, то дуга (a, b) помечена меткой L, иначе она помечена меткой L. Приведем алгоритм проверки принадлежности классу SLR, который одновременно производит разбиение (если это возможно) атрибутов каждого символа по обходам.

Алгоритм B.7.

* Построение функции проходов pass(a) атрибутов
символов,
* дающей либо минимальный номер прохода, на котором атрибут
* может быть вычислен, либо неопределено,
* если атрибут не может быть занесен ни в
* один из элементов разбиения A(X), aA(X).
begin строим граф LR предшествования для AG;
Полагаем COST(a) неопредел_нной для всех вершин a;
m := -1, repeat m := m + 1;
Положить COST(a) равной m для всех вершин,
  для которых COST(a) неопределено;
repeat для вершины a такой, что COST(a) = m
  положить COST(a) неопредел_нным;
Если существует вершина b и дуга (b, a) такие, что
  (COST(b) = m) and (B, a) имеет метку L)
  or (COST(b) неопределено)
  until нельзя найти такой вершины a,
    что COST(a) можно сделать неопредел_нным;
  until либо для всех a COST(a) вычислена,
  либо не существует вершины b такой,
    что COST(b) = m, для всех a принадлежит A
  if (COST(a) определено)
    then pass(a) := COST(a) + 1
    else pass(a) := неопределено
  end
end.

Этот алгоритм легко обобщается на простые многопроходные в обоих направлениях атрибутные грамматики [5].

Совсем простым частным случаем LR многопроходных атрибутных грамматик являются однопроходные атрибутные грамматики.

Теорема B.17. Атрибутная грамматика является LR однопроходной тогда и только тогда, когда ни один из графов братьев для правил вывода не содержит дуг из X в X для i >= j.

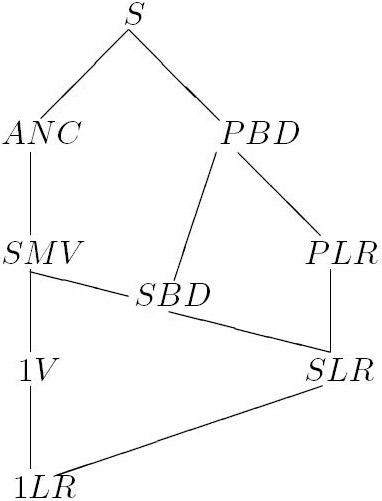
Таким образом между рассмотренными классами атрибутных грамматик имеет место включение, показанное на рис. B.7:

Рис. B.7.