Программная система ПараЛаб для изучения и исследования методов параллельных вычислений
12.4.5. Обработка графов
Математические модели в виде графов широко используются при моделировании самых разнообразных явлений, процессов и систем. Как результат, многие теоретические и реальные прикладные задачи могут быть решены при помощи тех или иных процедур анализа графовых моделей. Среди множества этих процедур может быть выделен некоторый определенный набор типовых алгоритмов обработки графов.
В системе ПараЛаб реализованы параллельные алгоритмы решения двух типовых задач на графах: алгоритм Прима для поиска минимального охватывающего дерева и алгоритм Дейкстры для поиска кратчайших путей. Более полная информация об алгоритмах обработки графов, реализованных в системе ПараЛаб, содержится в "Параллельные методы на графах" .
Правила использования системы ПараЛаб
1. Переход в режим редактирования графа. При выборе задачи Обработка графов в системе ПараЛаб предусмотрена возможность создания и редактирования графов, запоминания графов в файле и чтения графа из файла. Для того чтобы перейти в режим редактирования графа, выполните команду Формирование графа пункта меню Задача. Заметим, что команда доступна только в том случае, когда текущей задачей является задача обработки графов.
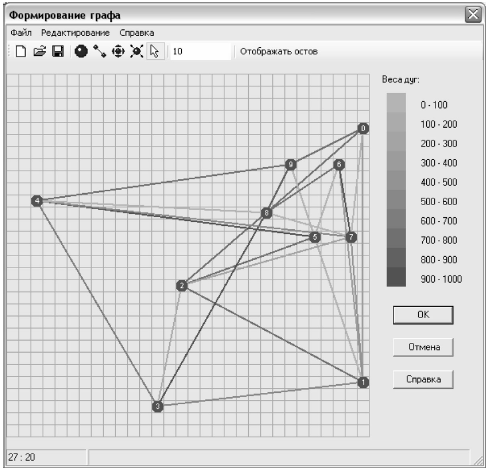
После выполнения команды Формирование графа на экране дисплея появляется новое окно (рис. 12.10), в рабочей области которого отображается граф активного эксперимента. Если граф в эксперимент не был загружен, то рабочая область окна пуста.
Вам предоставляется возможность создавать новые графы, редактировать уже существующие, сохранять новые графы в файлах и загружать графы из файлов в активный эксперимент.
2. Создание нового графа. Для создания нового пустого графа
выберите пункт меню Файл и выполните команду Новый (или щелкните
левой кнопкой мыши на иконке панели инструментов). Если граф,
который отображается в рабочей области, был изменен, то вам будет
предложено сохранить измененный граф в файл.
панели инструментов). Если граф,
который отображается в рабочей области, был изменен, то вам будет
предложено сохранить измененный граф в файл.
3. Открытие существующего графа. Для загрузки графа из файла
выберите пункт меню Файл и выполните команду Загрузить (или
щелкните левой кнопкой мыши на иконке панели инструментов). В
появившемся диалоговом окне выберите имя файла (файлы графов
ПараЛаб имеют расширение .plg) и нажмите кнопку Открыть.
панели инструментов). В
появившемся диалоговом окне выберите имя файла (файлы графов
ПараЛаб имеют расширение .plg) и нажмите кнопку Открыть.
4. Сохранение графа. Для сохранения графа в файл выберите
пункт меню Файл и выполните команду Сохранить (или щелкните левой
кнопкой мыши на иконке панели инструментов). В появившемся
диалоговом окне введите имя нового файла или выберите какой-либо
из существующих файлов для того, чтобы сохранить граф в этом
файле. Нажмите кнопку Сохранить.
панели инструментов). В появившемся
диалоговом окне введите имя нового файла или выберите какой-либо
из существующих файлов для того, чтобы сохранить граф в этом
файле. Нажмите кнопку Сохранить.
5. Редактирование графа. С графом, расположенным в рабочей области окна, можно производить различные операции.
- Для того чтобы добавить к графу одну или несколько новых
вершин, выберите пункт меню Редактирование и выполните команду Добавить вершину (или щелкните левой кнопкой мыши на иконке
 панели инструментов). При этом вид курсора изменится, над
указателем появится символическое изображение вершины. Рабочая
область окна представляет собой сетку. Щелкая левой кнопкой мыши
в различных клетках сетки, вы можете добавлять в граф новые
вершины. Если вы щелкнули в клетке, где уже есть вершина, то
добавления вершины не произойдет.
панели инструментов). При этом вид курсора изменится, над
указателем появится символическое изображение вершины. Рабочая
область окна представляет собой сетку. Щелкая левой кнопкой мыши
в различных клетках сетки, вы можете добавлять в граф новые
вершины. Если вы щелкнули в клетке, где уже есть вершина, то
добавления вершины не произойдет. - Для того чтобы соединить две вершины графа ребром, выберите
пункт меню Редактирование и выполните команду Добавить ребро (или
щелкните левой кнопкой мыши на иконке
 панели инструментов).
После этого курсор изменит форму, под указателем появится
изображение двух вершин, соединенных ребром. Выделите одну из
вершин графа, щелкнув на ней левой кнопкой мыши. Ее цвет
изменится на темно-красный. Выделите другую вершину графа – в
результате между первой и второй указанными вершинами появится
ребро. Вес ребра определяется случайным образом. Если между
первой и второй вершинами до редактирования существовало ребро,
то оно будет удалено.
панели инструментов).
После этого курсор изменит форму, под указателем появится
изображение двух вершин, соединенных ребром. Выделите одну из
вершин графа, щелкнув на ней левой кнопкой мыши. Ее цвет
изменится на темно-красный. Выделите другую вершину графа – в
результате между первой и второй указанными вершинами появится
ребро. Вес ребра определяется случайным образом. Если между
первой и второй вершинами до редактирования существовало ребро,
то оно будет удалено. - Для того чтобы переместить вершину графа, выберите пункт меню Редактирование и выполните команду Переместить вершину (или
щелкните левой кнопкой мыши на иконке
 панели инструментов).
После этого курсор изменит форму, примет вид, изображенный на
кнопке панели инструментов. Выделите одну из вершин графа,
щелкнув на ней левой кнопкой мыши. Цвет вершины изменится на
темно-красный. Перемещайте курсор мыши по рабочей области окна –
вы увидите, что вершина перемещается вслед за курсором. Щелкните
на любой пустой клетке рабочей области, и выделенная вершина
переместится в эту точку.
панели инструментов).
После этого курсор изменит форму, примет вид, изображенный на
кнопке панели инструментов. Выделите одну из вершин графа,
щелкнув на ней левой кнопкой мыши. Цвет вершины изменится на
темно-красный. Перемещайте курсор мыши по рабочей области окна –
вы увидите, что вершина перемещается вслед за курсором. Щелкните
на любой пустой клетке рабочей области, и выделенная вершина
переместится в эту точку. - Для того чтобы удалить вершину графа, выберите пункт меню Редактирование и выполните команду Удалить вершину (или щелкните
левой кнопкой мыши на иконке
 панели инструментов). После этого
курсор изменит вид, под указателем появится пиктограмма
перечеркнутой вершины. Щелкните левой кнопкой мыши на любой
вершине графа, чтобы удалить ее.
панели инструментов). После этого
курсор изменит вид, под указателем появится пиктограмма
перечеркнутой вершины. Щелкните левой кнопкой мыши на любой
вершине графа, чтобы удалить ее.
Для выхода из любого из режимов (Добавление вершины, Удаление
вершины, Перемещение вершины, Добавление ребра) щелкните левой
кнопкой мыши на иконке панели инструментов.
панели инструментов.
6. Формирование графа при помощи случайного механизма. Граф можно задавать при помощи случайного генератора. Для этого в редакторе, расположенном на панели инструментов, укажите число вершин графа, далее выберите пункт меню Редактирование и выполните команду Случайное формирование.
7. Редактирование веса ребра графа. Цвет ребер графа имеет разную интенсивность. Чем темнее цвет, тем больше вес ребра. Для того чтобы приблизительно определить вес ребра, нужно сравнить его цвет со шкалой, расположенной справа. Для того чтобы изменить вес ребра, щелкните на нем правой кнопкой мыши. Рядом с ребром появится ползунок. Перемещая его вправо, вы увеличиваете вес ребра, перемещая влево – уменьшаете. Для закрепления изменений щелкните мышкой в любой точке рабочей области или нажмите любую клавишу.
8. Выход из режима редактирования. Для загрузки текущего графа в активный эксперимент нажмите кнопку ОК. Для выхода без сохранения изменений нажмите кнопку Отмена.
12.4.5.1. Алгоритм Прима поиска минимального охватывающего дерева
Охватывающим деревом (или остовом ) неориентированного графа G называется подграф T графа G, который является деревом и содержит все вершины из G. Определим вес подграфа для взвешенного графа как сумму весов входящих в подграф дуг, тогда под минимально охватывающим деревом ( МОД ) Т будем понимать охватывающее дерево минимального веса. Содержательная интерпретация задачи нахождения МОД может состоять, например, в практическом примере построения локальной сети персональных компьютеров с прокладыванием наименьшего количества соединительных линий связи.
Дадим краткое описание алгоритма решения поставленной задачи, известного под названием метода Прима ( Prim ). Алгоритм начинает работу с произвольной вершины графа, выбираемой в качестве корня дерева, и в ходе последовательно выполняемых итераций расширяет конструируемое дерево до МОД. Распределение данных между процессорами вычислительной системы должно обеспечивать независимость перечисленных операций алгоритма Прима. В частности, это может быть реализовано, если каждая вершина графа располагается на процессоре вместе со всей связанной с вершиной информацией.
С учетом такого разделения данных итерация параллельного варианта алгоритма Прима состоит в следующем:
- определяется вершина, имеющая наименьшее расстояние до построенного к этому моменту МОД (операции вычисления расстояния для вершин графа, не включенных в МОД, независимы и, следовательно, могут быть выполнены параллельно);
- найденная вершина включается в состав МОД.
12.4.5.2. Алгоритм Дейкстры поиска кратчайших путей
Задача поиска кратчайших путей на графе состоит в нахождении путей минимального веса от некоторой заданной вершины S до всех имеющихся вершин графа. Постановка подобной проблемы имеет важное практическое значение в различных приложениях, когда веса дуг означают время, стоимость, расстояние, затраты и т.п.
Возможный способ решения поставленной задачи, известный как алгоритм Дейкстры, практически совпадает с методом Прима. Различие состоит лишь в интерпретации и в правиле оценки расстояний. В алгоритме Дейкстры эти величины означают суммарный вес пути от начальной вершины до всех остальных вершин графа. Как результат, на каждой итерации алгоритма выбирается очередная вершина, расстояние от которой до корня дерева минимально, и происходит включение этой вершины в дерево кратчайших путей.
Задания и упражнения
- Запустите систему ПараЛаб. В активном окне вычислительного эксперимента установите топологию Полный граф. Текущей задачей этого окна сделайте задачу обработки графов.
- Выполните команду Формирование графа пункта меню Задача. В появившемся редакторе графов сформируйте случайным образом граф с десятью вершинами.
- Выполните вычислительный эксперимент по поиску минимального охватывающего дерева с помощью алгоритма Прима (выполните команду Метод пункта меню Задача, в появившемся диалоговом окне выберите Метод Прима ).
- Проведите несколько экспериментов, изменяя количество процессоров. Изучите зависимость временных характеристик алгоритма Прима от количества процессоров.
- Проведите аналогичную последовательность экспериментов для изучения временных характеристик метода Дейкстры.