Программная система ПараЛаб для изучения и исследования методов параллельных вычислений

12.4.2. Умножение матрицы на вектор

В результате умножения матрицы А размерности mxn и вектора b, состоящего из n элементов, получается вектор c размера m, каждый i -й элемент которого есть результат скалярного умножения i -й строки матрицы А (обозначим эту строчку a_i ) и вектора b:

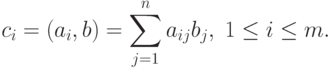
Тем самым получение результирующего вектора c предполагает повторение m однотипных операций по умножению строк матрицы A и вектора b. Каждая такая операция включает умножение элементов строки матрицы и вектора b ( n операций) и последующее суммирование полученных произведений ( n-1 операций). Общее количество необходимых скалярных операций есть величина

T1=mx(2n-1).

Для операции умножения матрицы на вектор характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Это свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов, и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами используемой вычислительной системы. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений; существование разных схем распределения данных порождает целый ряд параллельных алгоритмов матричных вычислений.

Наиболее общие и широко используемые способы разделения матриц состоят в разбиении данных на полосы (по вертикали или горизонтали) или на прямоугольные фрагменты ( блоки ).

Более полная информация об алгоритмах матрично-векторного умножения, реализованных в системе ПараЛаб, содержится в "Параллельные методы умножения матрицы на вектор" .

12.4.2.1. Умножение матрицы на вектор при разделении данных по строкам

Данный алгоритм основан на представлении матрицы непрерывными наборами (горизонтальными полосами) строк. Полученные полосы распределяются по процессорам вычислительной системы. Вектор b копируется на все процессоры. Перемножение полосы матрицы на вектор (а данная операция может быть выполнена процессорами параллельно) приводит к получению блока элементов результирующего вектора с. Для объединения результатов расчета и получения полного вектора c на каждом из процессоров вычислительной системы необходимо выполнить операцию обобщенного сбора данных.

Задания и упражнения

1. Создайте в системе ПараЛаб новое окно вычислительного эксперимента. Для этого окна выберите задачу умножения матрицы на вектор (щелкните левой кнопкой мыши на строке Умножение матрицы на вектор пункта меню Задача ).
2. Откройте диалоговое окно выбора метода и убедитесь в том, что выбран метод, основанный на горизонтальном разбиении матрицы.
3. Проведите несколько вычислительных экспериментов. Изучите зависимость времени выполнения алгоритма от объема исходных данных и от количества процессоров.

12.4.2.2. Умножение матрицы на вектор при разделении данных по столбцам

Другой подход к параллельному умножению матрицы на вектор основан на разделении исходной матрицы на непрерывные наборы (вертикальные полосы) столбцов. Вектор b при таком подходе разделен на блоки. Вертикальные полосы исходной матрицы и блоки вектора распределены между процессорами вычислительной системы.

Параллельный алгоритм умножения матрицы на вектор начинается с того, что каждый процессор i выполняет умножение своей вертикальной полосы матрицы А на блок элементов вектора b, в итоге на каждом процессоре получается вектор промежуточных результатов c'(i). Далее для получения элементов результирующего вектора с процессоры должны обменяться своими промежуточными данными между собой.

12.4.2.3. Умножение матрицы на вектор при блочном разделении данных

Рассмотрим теперь параллельный алгоритм умножения матрицы на вектор, который основан на ином способе разделения данных – на разбиении матрицы на прямоугольные фрагменты ( блоки ). При таком способе разделения данных исходная матрица A представляется в виде набора прямоугольных блоков. Вектор b также должен быть разделен на блоки. Блоки матрицы и блоки вектора распределены между процессорами вычислительной системы. Логическая (виртуальная) топология вычислительной системы в данном случае имеет вид прямоугольной двумерной решетки. Размеры процессорной решетки соответствуют количеству прямоугольных блоков, на которые разбита матрица A. На процессоре p_i,j, находящемся на пересечении i -й строки и j -го столбца процессорной решетки, располагается блок A_i,j матрицы A и блок b_j вектора b.

После перемножения блоков матрицы A и вектора b каждый процессор p_i,j будет содержать вектор частичных результатов c'_(i,j). Поэлементное суммирование векторов частичных результатов для каждой горизонтальной строки процессорной решетки позволяет получить результирующий вектор c.

Задания и упражнения

• Запустите систему ПараЛаб. Установите количество процессоров, равное четырем.
• Выполните три последовательных эксперимента с использованием трех различных алгоритмов умножения матрицы на вектор — алгоритмов, основанных на горизонтальном, вертикальном и блочном разбиении матрицы. Сравните временные характеристики алгоритмов, которые отображаются в правой нижней части окна. Убедитесь в том, что у алгоритмов, основанных на ленточном разбиении матрицы, время выполнения практически совпадает, а также в том, что время выполнения алгоритма, основанного на блочном разбиении, несколько больше.
• Измените объем исходных данных (выполните команду Параметры задачи пункта меню Задача ). Снова проведите эксперименты. Сравните временные характеристики алгоритмов.
• Измените количество процессоров, установите количество процессоров, равное 16 (выполните команду Количество процессоров пункта меню Система ). Проведите вычислительные эксперименты и сравните временные характеристики.