Решение систем линейных уравнений
8.4. Краткий обзор лекции
Данная лекция посвящена проблеме параллельных вычислений при решении систем линейных уравнений. Изложение учебного материала проводится с использованием двух широко известных алгоритмов: метода Гаусса как примера прямого алгоритма решения задачи и итерационного метода сопряженных градиентов.
Параллельный вариант метода Гаусса (подраздел 8.2) основывается на ленточном разделении матрицы между процессорами с использованием циклической схемы распределения строк, что позволяет сбалансировать вычислительную нагрузку. Для определения параллельного варианта метода проводится полный цикл проектирования – определяются базовые подзадачи, выделяются информационные взаимодействия, обсуждаются вопросы масштабирования, выводятся оценки показателей эффективности, предлагается схема программной реализации и приводятся результаты вычислительных экспериментов. Как видно из графика, представленного на рис. 8.8, параллельный алгоритм Гаусса демонстрирует достаточно высокие показатели ускорения и эффективности.
Важный момент при рассмотрении параллельного варианта метода сопряженных градиентов (подраздел 8.3) состоит в том, что способ параллельных вычислений для этого метода может быть получен через параллельные алгоритмы выполняемых вычислительных действий – операций умножения матрицы на вектор, скалярного произведения векторов, сложения и вычитания векторов. Выбранный для учебного примера подход состоит в распараллеливании вычислительно наиболее трудоемкой операции умножения матрицы на вектор, в то время как все вычисления над векторами дублируются на каждом процессоре для уменьшения числа выполняемых операций передачи данных — показатели эффективности подобного способа организации параллельных вычислений представлены на рис. 8.8.
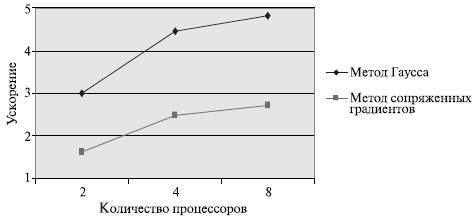
Рис. 8.8. Ускорение параллельных алгоритмов решения системы линейных уравнений с размером матрицы 3000x3000
8.5. Обзор литературы
Проблема численного решения систем линейных уравнений широко рассматривается в литературе. Для учебного рассмотрения могут быть рекомендованы работы [ [ 6 ] , [ 13 ] , [ 51 ] , [ 63 ] ]. Широкое обсуждение вопросов параллельных вычислений для решения данного типа задач выполнено в работах [ [ 22 ] , [ 30 ] ].
При рассмотрении вопросов программной реализации параллельных методов может быть рекомендована работа [ [ 23 ] ]. В ней рассматривается хорошо известная и широко используемая в практике параллельных вычислений программная библиотека численных методов ScaLAPACK.
8.6. Контрольные вопросы
- Что представляет собой система линейных уравнений? Какие типы систем вам известны? Какие методы могут быть использованы для решения систем разных типов?
- В чем состоит постановка задачи решения системы линейных уравнений?
- В чем идея параллельной реализации метода Гаусса?
- Какие информационные взаимодействия имеются между базовыми подзадачами для параллельного варианта метода Гаусса?
- Каковы показатели эффективности для параллельного варианта метода Гаусса?
- В чем состоит схема программной реализации параллельного варианта метода Гаусса?
- В чем состоит идея параллельной реализации метода сопряженных градиентов?
- Какой из алгоритмов обладает большей коммуникационной сложностью?
8.7. Задачи и упражнения
- Выполните анализ эффективности параллельных вычислений в отдельности для прямого и обратного этапов метода Гаусса. Оцените, на каком этапе происходит большее снижение показателей.
- Выполните разработку параллельного варианта метода Гаусса при вертикальном разбиении матрицы по столбцам. Постройте теоретические оценки времени работы этого алгоритма с учетом параметров используемой вычислительной системы. Проведите вычислительные эксперименты. Сравните результаты выполненных экспериментов с ранее полученными теоретическими оценками.
- Выполните реализацию параллельного метода сопряженных градиентов. Постройте теоретические оценки времени работы этого алгоритма с учетом параметров используемой вычислительной системы. Проведите вычислительные эксперименты. Сравните результаты выполненных экспериментов с ранее полученными теоретическими оценками.
- Выполните разработку параллельных вариантов методов Якоби и Зейделя решения систем линейных уравнений (см., например, Kumar (1994)). Постройте теоретические оценки времени работы этого алгоритма с учетом параметров используемой вычислительной системы. Проведите вычислительные эксперименты. Сравните результаты выполненных экспериментов с ранее полученными теоретическими оценками.
