Решение систем линейных уравнений
8.3. Метод сопряженных градиентов
Рассмотрим теперь совершенно иной подход к решению систем линейных уравнений, при котором к искомому точному решению x* системы Ax=b строится последовательность приближенных решений x0, x1, ..., xk, ... При этом процесс вычислений организуется таким способом, что каждое очередное приближение дает оценку точного решения со все уменьшающейся погрешностью, и при продолжении расчетов оценка точного решения может быть получена с любой требуемой точностью. Подобные итерационные методы решения систем линейных уравнений широко используются в практике вычислений. К преимуществам итерационных методов можно отнести меньший объем (по сравнению, например, с методом Гаусса) необходимых вычислений для решения разреженных систем линейных уравнений, возможность более быстрого получения начальных приближений искомого решения, наличие эффективных способов организации параллельных вычислений. Дополнительная информация с описанием таких методов, рассмотрением вопросов сходимости и точности получаемых решений может быть получена, например, в [ [ 6 ] , [ 22 ] ].
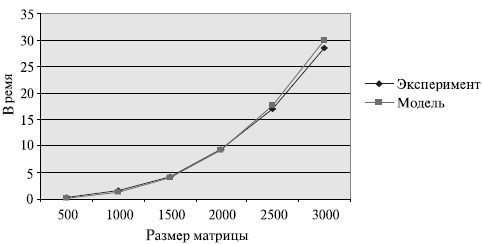
Рис. 8.4. График зависимости экспериментального и теоретического времени проведения эксперимента на двух процессорах от объема исходных данных
Одним из наиболее известных итерационных алгоритмов является метод сопряженных градиентов, который может быть применен для решения симметричной положительно определенной системы линейных уравнений большой размерности.
Напомним, что матрица А является симметричной, если она совпадает со своей транспонированной матрицей, т.е. А=АТ. Матрица А называется положительно определенной, если для любого вектора x справедливо: xTAx>0.
Известно (см., например, [ [ 6 ] , [ 22 ] ]), что после выполнения n итераций алгоритма ( n есть порядок решаемой системы линейных уравнений ), очередное приближение xn совпадает с точным решением.
8.3.1. Последовательный алгоритм
Если матрица A симметричная и положительно определенная, то функция
 |
( 8.6) |
Итерация метода сопряженных градиентов состоит в вычислении очередного приближения к точному решению в соответствии с правилом:
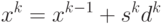 |
( 8.7) |
Тем самым, новое значение приближения xk вычисляется с учетом приближения, построенного на предыдущем шаге xk-1, скалярного шага sk и вектора направления dk.
Перед выполнением первой итерации векторы x0 и d0 полагаются равными нулю, а для вектора g0 устанавливается значение, равное - b. Далее каждая итерация для вычисления очередного значения приближения xk включает выполнение четырех шагов:
Шаг 1: Вычисление градиента:
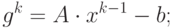 |
( 8.8) |
Шаг 2: Вычисление вектора направления:
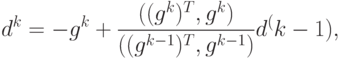
Шаг 3: Вычисление величины смещения по выбранному направлению:
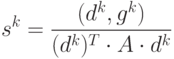 |
( 8.10) |
Шаг 4: Вычисление нового приближения:
 |
( 8.11) |
Как можно заметить, данные выражения включают две операции умножения матрицы на вектор, четыре операции скалярного произведения и пять операций над векторами. Как результат, общее количество операций, выполняемых на одной итерации, составляет
t1=2n2+13n.
Как уже отмечалось ранее, для нахождения точного решения системы линейных уравнений с положительно определенной симметричной матрицей необходимо выполнить n итераций. Таким образом, для нахождения решения системы необходимо выполнить
 |
( 8.12) |
Поясним выполнение метода сопряженных градиентов на примере решения системы линейных уравнений вида:
3x0 -x1 = 3, -x0 +3x1 = 7.
Эта система уравнений второго порядка обладает симметричной положительно определенной матрицей, для нахождения точного решения этой системы достаточно провести всего две итерации метода.
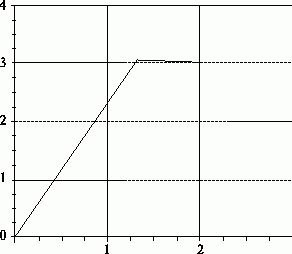
На первой итерации было получено значение градиента g1=(-3,-7), значение вектора направления d1=(3, 7), значение величины смещения s1=0,439. Соответственно, очередное приближение к точному решению системы x1=(1,318, 3,076).
На второй итерации было получено значение градиента g2=(-2,121, 0,909), значение вектора направления d2=(2,397, -0,266), а величина смещения – s2=0,284. Очередное приближение совпадает с точным решением системы x2=(2, 3).
На рис. 8.5 представлена последовательность приближений к точному решению, построенная методом сопряженных градиентов (в качестве начального приближения x0 выбрана точка (0,0) ).
8.3.2. Организация параллельных вычислений
При разработке параллельного варианта метода сопряженных градиентов для решения систем линейных уравнений в первую очередь следует учесть, что выполнение итераций метода осуществляется последовательно и, тем самым, наиболее целесообразный подход состоит в распараллеливании вычислений, реализуемых в ходе выполнения итераций.
Анализ соотношений (8.8) – (8.11) показывает, что основные вычисления, выполняемые в соответствии с методом, состоят в умножении матрицы A на векторы x и d, и, как результат, при организации параллельных вычислений может быть полностью использован материал, изложенный в "Параллельные методы умножения матрицы на вектор" .
Дополнительные вычисления в (8.8) – (8.11), имеющие меньший порядок сложности, представляют собой различные операции обработки векторов (скалярное произведение, сложение и вычитание, умножение на скаляр). Организация таких вычислений, конечно же, должна быть согласована с выбранным параллельным способом выполнения операции умножения матрицы на вектор. Общие же рекомендации могут состоять в следующем: при малом размере векторов можно применить дублирование векторов между процессорами, при большом порядке решаемой системы линейных уравнений более целесообразно осуществлять блочное разделение векторов.