Параллельное программирование на основе MPI
5.7. Виртуальные топологии
Под топологией вычислительной системы обычно понимается структура узлов сети и линий связи между этими узлами. Топология может быть представлена в виде графа, в котором вершины есть процессоры ( процессы ) системы, а дуги соответствуют имеющимся линиям (каналам) связи.
Как уже отмечалось ранее, парные операции передачи данных могут быть выполнены между любыми процессами одного и того же коммуникатора, а в коллективной операции принимают участие все процессы коммуникатора. В этом плане, логическая топология линий связи между процессами в параллельной программе имеет структуру полного графа (независимо от наличия реальных физических каналов связи между процессорами).
Понятно, что физическая топология системы является аппаратно реализуемой и изменению не подлежит (хотя существуют и программируемые средства построения сетей). Но, оставляя неизменной физическую основу, мы можем организовать логическое представление любой необходимой виртуальной топологии. Для этого достаточно, например, сформировать тот или иной механизм дополнительной адресации процессов.
Использование виртуальных процессов может оказаться полезным в силу ряда разных причин. Виртуальная топология, например, может больше соответствовать имеющейся структуре линий передачи данных. Применение виртуальных топологий может заметно упростить в ряде случаев представление и реализацию параллельных алгоритмов.
В MPI поддерживаются два вида топологий – прямоугольная решетка произвольной размерности ( декартова топология ) и топология графа произвольного вида. Следует отметить, что имеющиеся в MPI функции обеспечивают лишь получение новых логических систем адресации процессов, соответствующих формируемым виртуальным топологиям. Выполнение же всех коммуникационных операций должно осуществляться, как и ранее, при помощи обычных функций передачи данных с использованием исходных рангов процессов.
5.7.1. Декартовы топологии (решетки)
Декартовы топологии, в которых множество процессов представляется в виде прямоугольной решетки (см. п. 1.4.1 и рис. 1.7), а для указания процессов используется декартова система координат, широко применяются во многих задачах для описания структуры имеющихся информационных зависимостей. В числе примеров таких задач – матричные алгоритмы (см. лекции "Параллельные методы умножения матрицы на вектор" и "Параллельные методы матричного умножения" ) и сеточные методы решения дифференциальных уравнений в частных производных (см. "Параллельные методы решения дифференциальных уравнений в частных производных" ).
Для создания декартовой топологии (решетки) в MPI предназначена функция:
int MPI_Cart_create(MPI_Comm oldcomm, int ndims, int *dims, int *periods, int reorder, MPI_Comm *cartcomm),
где
- oldcomm — исходный коммуникатор;
- ndims — размерность декартовой решетки;
- dims — массив длины ndims, задает количество процессов в каждом измерении решетки;
- periods — массив длины ndims, определяет, является ли решетка периодической вдоль каждого измерения;
- reorder — параметр допустимости изменения нумерации процессов ;
- cartcomm — создаваемый коммуникатор с декартовой топологией процессов.
Операция создания топологии является коллективной и, тем самым, должна выполняться всеми процессами исходного коммуникатора.
Для пояснения назначения параметров функции MPI_Cart_create рассмотрим пример создания двумерной решетки 4x4, в которой строки и столбцы имеют кольцевую структуру (за последним процессом следует первый процесс ):
// Создание двумерной решетки 4x4 MPI_Comm GridComm; int dims[2], periods[2], reorder = 1; dims[0] = dims[1] = 4; periods[0] = periods[1] = 1; MPI_Cart_create(MPI_COMM_WORLD, 2, dims, periods, reorder, &GridComm);
Следует отметить, что в силу кольцевой структуры измерений сформированная в рамках примера топология является тором.
Для определения декартовых координат процесса по его рангу можно воспользоваться функцией:
int MPI_Cart_coords(MPI_Comm comm, int rank, int ndims, int *coords),
где
- comm — коммуникатор с топологией решетки;
- rank — ранг процесса, для которого определяются декартовы координаты;
- ndims — размерность решетки;
- coords — возвращаемые функцией декартовы координаты процесса.
Обратное действие – определение ранга процесса по его декартовым координатам – обеспечивается при помощи функции:
int MPI_Cart_rank(MPI_Comm comm, int *coords, int *rank),
где
- comm — коммуникатор с топологией решетки;
- coords — декартовы координаты процесса ;
- rank — возвращаемый функцией ранг процесса.
Полезная во многих приложениях процедура разбиения решетки на подрешетки меньшей размерности обеспечивается при помощи функции:
int MPI_Cart_sub(MPI_Comm comm, int *subdims, MPI_Comm *newcomm),
где
- comm — исходный коммуникатор с топологией решетки;
- subdims — массив для указания, какие измерения должны остаться в создаваемой подрешетке;
- newcomm — создаваемый коммуникатор с подрешеткой.
Операция создания подрешеток также является коллективной и, тем самым, должна выполняться всеми процессами исходного коммуникатора. В ходе своего выполнения функция MPI_Cart_sub определяет коммуникаторы для каждого сочетания координат фиксированных измерений исходной решетки.
Для пояснения функции MPI_Cart_sub дополним ранее рассмотренный пример создания двумерной решетки и определим коммуникаторы с декартовой топологией для каждой строки и столбца решетки в отдельности:
// Создание коммуникаторов для каждой строки и столбца решетки MPI_Comm RowComm, ColComm; int subdims[2]; // Создание коммуникаторов для строк subdims[0] = 0; // фиксации измерения subdims[1] = 1; // наличие данного измерения в подрешетке MPI_Cart_sub(GridComm, subdims, &RowComm); // Создание коммуникаторов для столбцов subdims[0] = 1; subdims[1] = 0; MPI_Cart_sub(GridComm, subdims, &ColComm);
В приведенном примере для решетки размером 4х4 создаются 8 коммуникаторов, по одному для каждой строки и столбца решетки. Для каждого процесса определяемые коммуникаторы RowComm и ColComm соответствуют строке и столбцу процессов, к которым данный процесс принадлежит.
Дополнительная функция MPI_Cart_shift обеспечивает поддержку процедуры последовательной передачи данных по одному из измерений решетки ( операция сдвига данных – см. "Оценка коммуникационной трудоемкости параллельных алгоритмов" ). В зависимости от периодичности измерения решетки, по которому выполняется сдвиг, различаются два типа данной операции:
-
циклический сдвиг на k
элементов вдоль измерения решетки – в этой операции данные от процесса i пересылаются процессу
 , где dim есть размер измерения, вдоль
которого производится сдвиг;
, где dim есть размер измерения, вдоль
которого производится сдвиг; - линейный сдвиг на k позиций вдоль измерения решетки – в этом варианте операции данные от процесса i пересылаются процессу i+k (если таковой существует).
Функция MPI_Cart_shift обеспечивает получение рангов процессов, с которыми текущий процесс ( процесс, вызвавший функцию MPI_Cart_shift ) должен выполнить обмен данными:
int MPI_Cart_shift(MPI_Comm comm, int dir, int disp, int *source, int *dst),
где
- comm — коммуникатор с топологией решетки;
- dir — номер измерения, по которому выполняется сдвиг;
- disp — величина сдвига (при отрицательных значениях сдвиг производится к началу измерения);
- source — ранг процесса, от которого должны быть получены данные;
- dst — ранг процесса, которому должны быть отправлены данные.
Следует отметить, что функция MPI_Cart_shift только определяет ранги процессов, между которыми должен быть выполнен обмен данными в ходе операции сдвига. Непосредственная передача данных может быть выполнена, например, при помощи функции MPI_Sendrecv.
5.7.2. Топологии графа
Сведения по функциям MPI для работы с виртуальными топологиями типа граф будут рассмотрены более кратко – дополнительная информация может быть получена, например, в [ [ 4 ] , [ 40 ] – [ 42 ] , [ 57 ] ].
Для создания коммуникатора с топологией типа граф в MPI предназначена функция:
int MPI_Graph_create(MPI_Comm oldcom, int nnodes, int *index, int *edges, int reorder, MPI_Comm *graphcom),
где
- oldcom — исходный коммуникатор;
- nnodes — количество вершин графа;
- index — количество исходящих дуг для каждой вершины;
- edges — последовательный список дуг графа;
- reorder — параметр допустимости изменения нумерации процессов ;
- graphcom – создаваемый коммуникатор с топологией типа граф.
Операция создания топологии является коллективной и, тем самым, должна выполняться всеми процессами исходного коммуникатора.
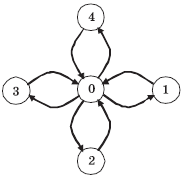
Для примера создадим топологию графа со структурой, представленной на рис. 5.9. В этом случае количество процессов равно 5, порядки вершин (количества исходящих дуг) принимают значения (4, 1, 1, 1, 1), а матрица инцидентности (номера вершин, для которых дуги являются входящими) имеет вид:
Для создания топологии с графом данного вида необходимо выполнить следующий программный код:
/* Создание топологии типа звезда */
int index[] = { 4,1,1,1,1 };
int edges[] = { 1,2,3,4,0,0,0,0 };
MPI_Comm StarComm;
MPI_Graph_create(MPI_COMM_WORLD, 5, index, edges, 1, &StarComm);Приведем еще две полезные функции для работы с топологиями графа. Количество соседних процессов, в которых от проверяемого процесса есть выходящие дуги, может быть получено при помощи функции:
int MPI_Graph_neighbors_count(MPI_Comm comm, int rank, int *nneighbors),
где
- comm — коммуникатор с топологией типа граф;
- rank — ранг процесса в коммуникаторе;
- nneighbors — количество соседних процессов.
Получение рангов соседних вершин обеспечивается функцией:
int MPI_Graph_neighbors(MPI_Comm comm, int rank, int mneighbors, int *neighbors),
где