Параллельное программирование на основе MPI
5.5. Производные типы данных в MPI
Во всех ранее рассмотренных примерах использования функций передачи данных предполагалось, что сообщения представляют собой некоторый непрерывный вектор элементов предусмотренного в MPI типа (список имеющихся в MPI типов представлен в табл. 5.1). Понятно, что в общем случае необходимые к пересылке данные могут рядом не располагаться и состоять из значений разных типов. Конечно, и в этих ситуациях разрозненные данные могут быть переданы с использованием нескольких сообщений, но такой способ решения неэффективен в силу накопления латентностей множества выполняемых операций передачи данных. Другой возможный подход состоит в предварительной упаковке передаваемых данных в формат того или иного непрерывного вектора, однако и здесь появляются лишние операции копирования данных, да и понятность таких операций передачи далека от желаемой.
| Вид коллективной операции | Общее описание и оценка сложности | Функции MPI | Примеры использования |
|---|---|---|---|
| Передача от одного процесса всем процессам (широковещательная рассылка) | п. 3.2.2 | MPI_Bcast п. 5.2.3.1 | п. 5.2.3.1 |
| Сбор и обработка данных на одном процессе от всех процессов (редукция данных) | пп. 3.2.2, 3.2.3 | MPI_Reduce п. 5.2.3.2 | п. 5.2.3.2 |
| - то же с рассылкой результатов всем процессам | пп. 3.2.2, 3.2.3 | MPI_Allreduce MPI_Reduce_scatter п. 5.4.4 | |
| - то же с получением частичных результатов обработки | пп. 3.2.2, 3.2.3 | MPI_Scan п. 5.4.4 | |
| Обобщенная передача от одного процесса всем процессам (распределение данных) | п. 3.2.4 | MPI_Scatter MPI_Scatterv п. 5.4.1 | "Параллельные методы умножения матрицы на вектор" |
| Обобщенная передача от всех процессов одному процессу (сбор данных) | п. 3.2.4 | MPI_Gather MPI_Gatherv п. 5.4.2 | "Параллельные методы умножения матрицы на вектор" |
| - то же с рассылкой результатов всем процессам | п. 3.2.4 | MPI_Allgather MPI_Allgatherv п. 5.4.2 | |
| Обобщенная передача данных от всех процессов всем процессам | п. 3.2.5 | MPI_Alltoall MPI_Alltoallv п. 5.4.3 | "Параллельные методы умножения матрицы на вектор" |
Для обеспечения больших возможностей при определении состава передаваемых сообщений в MPI предусмотрен механизм так называемых производных типов данных. Далее будут даны основные понятия используемого подхода, приведены возможные способы конструирования производных типов данных и рассмотрены функции упаковки и распаковки данных.
5.5.1. Понятие производного типа данных
В самом общем виде под производным типом данных в MPI можно понимать описание набора значений предусмотренного в MPI типа, причем в общем случае описываемые значения не обязательно непрерывно располагаются в памяти. Задание типа в MPI принято осуществлять при помощи карты типа ( type map ) в виде последовательности описаний входящих в тип значений; каждое отдельное значение описывается указанием типа и смещения адреса месторасположения от некоторого базового адреса, т.е.
TypeMap = {(type0, disp0),...,(typen-1, dispn-1)}.Часть карты типа с указанием только типов значений именуется в MPI сигнатурой типа:
TypeSignature = {type0,...,typen-1}.Сигнатура типа описывает, какие базовые типы данных образуют некоторый производный тип данных MPI, и, тем самым, управляет интерпретацией элементов данных при передаче или получении сообщений. Смещения карты типа определяют, где находятся значения данных.
Поясним рассмотренные понятия на следующем примере. Пусть в сообщение должны входить значения переменных:
double a; /* адрес 24 */ double b; /* адрес 40 */ int n; /* адрес 48 */
Тогда производный тип для описания таких данных должен иметь карту типа следующего вида:
{(MPI_DOUBLE, 0),
(MPI_DOUBLE, 16),
(MPI_INT, 24)}Дополнительно для производных типов данных в MPI используется следующий ряд новых понятий:
- нижняя граница типа
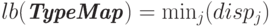 ;
; - верхняя граница типа
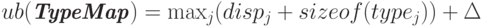 ;
; - протяженность типа
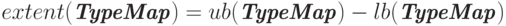 .
.
Согласно определению, нижняя граница есть смещение для первого байта значений рассматриваемого типа данных. Соответственно, верхняя граница представляет собой смещение для байта, располагающегося вслед за последним элементом рассматриваемого типа данных. При этом величина смещения для верхней границы может быть округлена вверх с учетом требований выравнивания адресов. Так, одно из требований, которые налагают некоторые реализации языков C и Fortran, состоит в том, чтобы адрес элемента был кратен длине этого элемента в байтах. Например, если тип int занимает четыре байта, то адрес элемента типа int должен нацело делиться на четыре. Именно это требование и отражается в определении верхней границы типа данных MPI. Поясним данный момент на ранее рассмотренном примере набора переменных a, b и n, для которого нижняя граница равна 0, а верхняя принимает значение 32 (величина округления 6 или 4 в зависимости от размера типа int ). Здесь следует отметить, что требуемое выравнивание определяется по типу первого элемента данных в карте типа.
Следует также указать на различие понятий "протяженность" и "размер типа". Протяженность – это размер памяти в байтах, который нужно отводить для одного элемента производного типа. Размер типа данных – это число байтов, которые занимают данные (разность между адресами последнего и первого байтов данных). Различие в значениях протяженности и размера опять же в величине округления для выравнивания адресов. Так, в рассматриваемом примере размер типа равен 28, а протяженность – 32 (предполагается, что тип int занимает четыре байта).
Для получения значения протяженности типа в MPI предусмотрена функция:
int MPI_Type_extent(MPI_Datatype type, MPI_Aint *extent),
где
- type — тип данных, протяженность которого отыскивается;
- extent — протяженность типа.
Размер типа можно найти, используя функцию:
int MPI_Type_size(MPI_Datatype type, MPI_Aint *size),
где
- type — тип данных, размер которого отыскивается;
- size — размер типа.
Определение нижней и верхней границ типа может быть выполнено при помощи функций:
int MPI_Type_lb(MPI_Datatype type, MPI_Aint *disp) и int MPI_Type_ub(MPI_Datatype type, MPI_Aint *disp),
где
- type — тип данных, нижняя граница которого отыскивается;
- disp — нижняя/верхняя граница типа.
Важной и необходимой при конструировании производных типов является функция получения адреса переменной:
int MPI_Address(void *location, MPI_Aint *address),
где
(следует отметить, что данная функция является переносимым вариантом средств получения адресов в алгоритмических языках C и Fortran ).
5.5.2. Способы конструирования производных типов данных
Для снижения сложности в MPI предусмотрено несколько различных способов конструирования производных типов:
- непрерывный способ позволяет определить непрерывный набор элементов существующего типа как новый производный тип;
- векторный способ обеспечивает создание нового производного типа как набора элементов существующего типа, между элементами которого имеются регулярные промежутки по памяти. При этом размер промежутков задается в числе элементов исходного типа, в то время как в варианте H-векторного способа этот размер указывается в байтах;
- индексный способ отличается от векторного метода тем, что промежутки между элементами исходного типа могут иметь нерегулярный характер (имеется и H-индексный способ, отличающийся способом задания промежутков);
- структурный способ обеспечивает самое общее описание производного типа через явное указание карты создаваемого типа данных.
Далее перечисленные способы конструирования производных типов данных будут рассмотрены более подробно.
5.5.2.1. Непрерывный способ конструирования
При непрерывном способе конструирования производного типа данных в MPI используется функция:
int MPI_Type_contiguous(int count, MPI_Data_type oldtype, MPI_Datatype *newtype),
где
- count — количество элементов исходного типа;
- oldtype — исходный тип данных;
- newtype — новый определяемый тип данных.
Как следует из описания, новый тип newtype создается как count элементов исходного типа oldtype. Например, если исходный тип данных имеет карту типа
{(MPI_INT, 0), (MPI_DOUBLE, 8)},то вызов функции MPI_Type_contiguous с параметрами
MPI_Type_contiguous(2, oldtype, &newtype);
приведет к созданию типа данных с картой типа
{(MPI_INT, 0), (MPI_DOUBLE, 8), (MPI_INT, 16), (MPI_DOUBLE, 24)}.В определенном плане наличие непрерывного способа конструирования является избыточным, поскольку использование аргумента count в процедурах MPI равносильно использованию непрерывного типа данных такого же размера.
5.5.2.2. Векторный способ конструирования
При векторном способе конструирования производного типа данных в MPI применяются функции
int MPI_Type_vector(int count, int blocklen, int stride, MPI_Data_type oldtype, MPI_Datatype *newtype) и int MPI_Type_hvector(int count, int blocklen, MPI_Aint stride, MPI_Data_type oldtype, MPI_Datatype *newtype),
где
- count — количество блоков;
- blocklen — размер каждого блока;
- stride — количество элементов, расположенных между двумя соседними блоками;
- oldtype — исходный тип данных;
- newtype — новый определяемый тип данных.
Отличие способа конструирования, определяемого функцией MPI_Type_hvector, состоит лишь в том, что параметр stride для определения интервала между блоками задается в байтах, а не в элементах исходного типа данных.
Как следует из описания, при векторном способе новый производный тип создается как набор блоков из элементов исходного типа, при этом между блоками могут иметься регулярные промежутки по памяти. Приведем несколько примеров использования данного способа конструирования типов:
- конструирование типа для выделения половины (только четных или только нечетных) строк матрицы размером nxn:
MPI_Type_vector(n / 2, n, 2 * n, &StripRowType, &ElemType),
- конструирование типа для выделения столбца матрицы размером nxn:
MPI_Type_vector(n, 1, n, &ColumnType, &ElemType),
- конструирование типа для выделения главной диагонали матрицы размером nxn:
MPI_Type_vector(n, 1, n + 1, &DiagonalType, &ElemType).
С учетом характера приводимых примеров можно упомянуть имеющуюся в MPI возможность создания производных типов для описания подмассивов многомерных массивов при помощи функции (данная функция предусматривается стандартом MPI -2):
int MPI_Type_create_subarray(int ndims, int *sizes, int *subsizes, int *starts, int order, MPI_Data_type oldtype, MPI_Datatype *newtype),
где
- ndims — размерность массива;
- sizes — количество элементов в каждой размерности исходного массива;
- subsizes — количество элементов в каждой размерности определяемого подмассива;
- starts — индексы начальных элементов в каждой размерности определяемого подмассива;
- order — параметр для указания необходимости переупорядочения;
- oldtype — тип данных элементов исходного массива;
- newtype — новый тип данных для описания подмассива.
