Применение теории нечетких множеств для обработки данных
Цель лекции: Ознакомиться с основными понятиями нечеткой логики способами ее применения к обработке экспериментальных данных.
Построение моделей приближенных размышлений человека и использование их в компьютерных системах представляет сегодня одну из важнейших проблем науки.
Для реальных сложных систем характерно наличие одновременно разнородной информации:
- точечных замеров и значений параметров;
- допустимых интервалов их изменения;
- статистических законов распределения для отдельных величин;
- лингвистических критериев и ограничений, полученных от специалистов-экспертов и т.д.
Наличие в сложной многоуровневой иерархической системе управления одновременно различных видов неопределенности делает необходимым использование для принятия решений теории нечетких множеств, которая позволяет адекватно учесть имеющиеся виды неопределенности.
Соответственно и вся информация о режимах функционирования подсистем, областях допустимости и эффективности, целевых функциях, предпочтительности одних режимов работы перед другими, о риске работы на каждом из режимов для подсистем и т.д. должна быть преобразована к единой форме и представлена в виде функций принадлежности. Такой подход позволяет свести воедино всю имеющуюся неоднородную информацию: детерминированную, статистическую, лингвистическую и интервальную.
Большая часть существующих методов для облегчения количественного исследования в рамках конкретных задач принятия решений базируется на крайне упрощенных моделях действительности и излишне жестких ограничениях, что уменьшает ценность результатов исследований и часто приводит к неверным решениям.
Применение для оперирования с неопределенными величинами аппарата теории вероятности приводит к тому, что фактически неопределенность, независимо от ее природы, отождествляется со случайностью, между тем как основным источником неопределенности во многих процессах принятия решений является нечеткость или расплывчатость (fuzzines).
В отличие от случайности, которая связана с неопределенностью, касающейся принадлежности или непринадлежности некоторого объекта к не расплывчатому множеству, понятие "нечеткость" относится к классам, в которых могут быть различные градации степени принадлежности, промежуточные между полной принадлежностью и непринадлежностью объектов к данному классу.
Вопрос выбора адекватного формального языка является очень важным, поэтому следует отметить преимущества описания процесса принятия решений в сложной многоуровневой иерархической системе на основе теории нечетких множеств. Этот язык дает возможность адекватно отразить сущность самого процесса принятия решений в нечетких условиях для многоуровневой системы, оперировать с нечеткими ограничениями и целями, а также задавать их с помощью лингвистических переменных.
В классической теории множеств непустое подмножество А из универсального множества Х однозначно определяется характеристическим функционалом [25]
 |
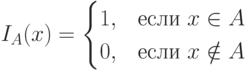( 12.1) |
Задание некоторого множества в этом случае эквивалентно заданию его характеристического функционала, поэтому все операции над множествами можно выразить через действия над их характеристическими функционалами.
Основные операции объединения, пересечения и разности двух подмножеств 
и 
из 
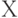с характеристическими функционалами 
и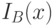 
соответственно определяются следующим образом для каждого 
:
 |
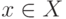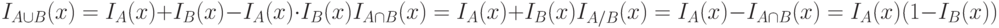( 12.2) |
Операции объединения и пересечения могут быть записаны в несколько ином виде:
 |
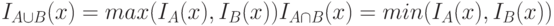( 12.3) |
Однако такие понятия, как множество "больших" или "малых величин", уже не являются множествами в классическом смысле, так как не определены границы их степеней малости, которые позволили бы провести классификационную процедуру (12.1) и четко отнести каждый объект к определенному классу. Большинство классов реальных объектов и процессов относятся именно к такому нечетко определенному типу. Поэтому возникает необходимость введения понятия о нечетком подмножестве как о классе с непрерывной градацией степеней принадлежности.
Для нечеткого подмножества, являющегося расширением понятия множества в классическом смысле, на пространстве объектов Х={x} вводится уже не функционал вида (12.1), а характеристическая функция. Она задает для всех элементов степень наличия у них некоторого свойства, по которому они относятся к подмножеству . Эта характеристическая функция для нечеткого множества традиционно носит название функции принадлежности .