Общие сведения об экспериментальных исследованиях
При обработке числовых массивов результатов эксперимента, как случайных величин, на практике применяют следующие выборочные оценки [ 24 ] :
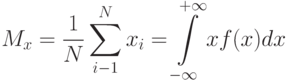 |
( 1.1) |
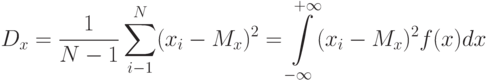 |
( 1.2) |
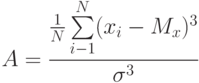 |
( 1.3) |
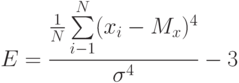 |
( 1.4) |
где  значение результата в
значение результата в 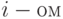 опыте;
опыте;  - число результатов в массиве;
- число результатов в массиве; 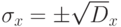 - среднеквадратичное отклонение.
- среднеквадратичное отклонение.
Производная оценка от величины математического ожидания и дисперсии является коэффициент вариации, определяемый в процентах по формуле:
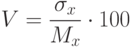 |
( 1.5) |
Дисперсия, среднее квадратичное отклонение и коэффициент вариации являются количественными характеристиками, оценки рассеивания значений результатов эксперимента как случайной величины и применяются при изучении различных действий со случайным исходом. Коэффициент асимметрии и коэффициент эксцесса являются характеристиками высшего порядка. Первый характеризует "скошенность распределения", а второй – степень его "островершинности"
Вычисленные по экспериментально наблюдаемым случайным величинам и случайным функциям статистические характеристики несут информацию не обо всей генеральной совокупности, которая в общем случае бесконечна, а лишь о некоторой ее части — выборке, элементы которой измерены с определенными ошибками. В связи с этим в результате эксперимента получают лишь некоторые оценки параметров генеральной совокупности.
Следовательно, и любая выборочная оценка — это случайная величина, точность определения которой и возможные при этом ошибки необходимо контролировать. Следует также иметь в виду, что вычисленные моменты распределения являются точечными оценками выборочных величин, так как каждый из них оценивает параметры генеральной совокупности с помощью единственного числа. Они позволяют судить о значении вычисленной статистической характеристики в данной точке и ничего не говорят о возможных пределах варьирования самой оценки.
К вычисляемым в результате эксперимента оценкам случайных величин предъявляются три основных требования: состоятельности, несмещенности и эффективности. Полагают, что оценка состоятельна, если с ростом объема выборки она стремится по вероятности к истинному значению, несмещена, если ее математическое ожидание стремится к истинному значению, и эффективна, когда оценка обладает наименьшим рассеянием по сравнению с любыми другими оценками. Из двух оценок эффективнее та, которая обладает меньшей дисперсией, т. е. значения которой рассеиваются в более узком интервале.
На уровень рассеивания оценок значительное влияние оказывают ошибки, имеющие место при эксперименте.
При выборочном наблюдении встречаются ошибки трех видов: грубые, систематические и случайные.
Грубые ошибки, отличающиеся большим отклонением от центра группирования выборки, отсеиваются на этапе первичного анализа материалов.
Точность измерений любой физической величины характеризуется, абсолютной 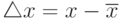 и относительной
и относительной 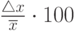 ошибками (здесь
ошибками (здесь  -истинное значение), которые, в свою очередь, состоят из суммы систематических
-истинное значение), которые, в свою очередь, состоят из суммы систематических  и случайных
и случайных  ошибок
ошибок
Систематические ошибки  постоянны при определении каждого члена выборки и зависят от технического уровня измерительной аппаратуры и техники эксперимента. Эти ошибки можно свести к минимуму периодической тарировкой приборов с помощью более совершенных и повышением точности метода определения исследуемых переменных. Случайные ошибки обусловлены влиянием большого количества факторов. Их появление неодинаково и случайно от измерения к измерению и не может быть предварительно учтено из-за их зависимости от изменения условий измерений и изменчивости самих измеряемых величин. Однако при достаточно большом количестве экспериментов суммарное значение случайных ошибок, изменяющихся примерно одинаково в положительную и отрицательную сторону, приближается к нулю. Случайные ошибки в подавляющем большинстве подчиняются нормальному закону распределения с математическим ожиданием, равным "0".
постоянны при определении каждого члена выборки и зависят от технического уровня измерительной аппаратуры и техники эксперимента. Эти ошибки можно свести к минимуму периодической тарировкой приборов с помощью более совершенных и повышением точности метода определения исследуемых переменных. Случайные ошибки обусловлены влиянием большого количества факторов. Их появление неодинаково и случайно от измерения к измерению и не может быть предварительно учтено из-за их зависимости от изменения условий измерений и изменчивости самих измеряемых величин. Однако при достаточно большом количестве экспериментов суммарное значение случайных ошибок, изменяющихся примерно одинаково в положительную и отрицательную сторону, приближается к нулю. Случайные ошибки в подавляющем большинстве подчиняются нормальному закону распределения с математическим ожиданием, равным "0".
В практике исследований систематические и случайные ошибки близки друг к другу и совместно определяют ошибку измерений. При оценке точности измерений рекомендуется учитывать суммарную ошибку
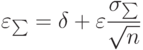 |
( 1.6) |
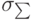 — среднеквадратическое отклонение случайной величины при числе измерений n.
— среднеквадратическое отклонение случайной величины при числе измерений n. Для величин, определяемых косвенно — методом расчета по другим измеренным случайным величинам, оценка погрешностей осуществляется вычислением статистических оценок по соответствующим функциональным зависимостям.
Выборочные характеристики 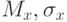 определяемые на основе ограниченного числа наблюдений, могут приближаться к истинным значениям характеристик генеральной совокупности
определяемые на основе ограниченного числа наблюдений, могут приближаться к истинным значениям характеристик генеральной совокупности 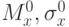 лишь с определенной точностью:
лишь с определенной точностью:
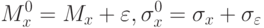 |
( 1.7) |
Точность выборочного наблюдения (эксперимента) может задаваться в единицах измерения исследуемой величины, в единицах выборочного значения 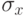 и в процентах исследуемой величины или характеристики.
и в процентах исследуемой величины или характеристики.
Систематическая ошибка, будучи постоянной, при этом может не учитываться.
Вероятность того, что истинное значение характеристик генеральной совокупности находится в отмеченных пределах, равна
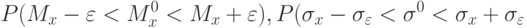 |
( 1.8) |
Так как математическое ожидание любой выборки само является случайной величиной, то полезно установить такой интервал, в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра.
Интервал 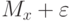 , в который в общем случае может быть произвольным
, в который в общем случае может быть произвольным ![[a_i,b_i]](/sites/default/files/tex_cache/e10d95fb27713b5a7bc1799bf6486aaf.png) , называется доверительными границами, а соответствующая вероятность - доверительной вероятностью или, как часто говорят, надежностью. Доверительную вероятность для удобства обозначают как
, называется доверительными границами, а соответствующая вероятность - доверительной вероятностью или, как часто говорят, надежностью. Доверительную вероятность для удобства обозначают как
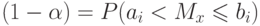 |
( 1.9) |
Соответственно  есть вероятность ошибки, которая на кривой распределения изображается в виде двух половинок
есть вероятность ошибки, которая на кривой распределения изображается в виде двух половинок 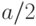 .
.
Вероятность ошибки характеризует долю риска в оценке истинного значения оцениваемой величины и часто называется уровнем значимости. Для удобства величину доверительного интервала устанавливают в долях среднеквадратического отклонения  . Тогда доверительную вероятность определяют, как площадь, ограниченную кривой нормального распределения на интервале
. Тогда доверительную вероятность определяют, как площадь, ограниченную кривой нормального распределения на интервале  . Используя формулу стандартного нормального распределения (9)
. Используя формулу стандартного нормального распределения (9)
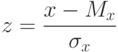 |
( 1.10) |
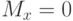 и
и 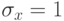
доверительную вероятность, согласно (8), записывают в таком виде:
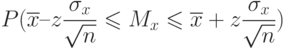 |
( 1.11) |
 - оценка среднего значения генеральной совокупности
- оценка среднего значения генеральной совокупности доверительный интервал для дисперсии
![[ \frac {n\sigma_x^2} {x^2 \alpha/2} \leqslant D_x \leqslant \frac {n\sigma_x^2} {x^21- \alpha/2}]](/sites/default/files/tex_cache/7a79e764121919f845ece34c05a116c1.png) |
( 1.12) |
Определяют доверительный интервал в такой последовательности: вычисляют параметр выборки 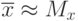 , выбирают доверительную вероятность,
, выбирают доверительную вероятность,  определяют соответствующее выбранному значению
определяют соответствующее выбранному значению  число из таблицы табулированных значений стандартного нормального распределения; вычисляют доверительный интервал
число из таблицы табулированных значений стандартного нормального распределения; вычисляют доверительный интервал 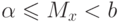 .
.
С увеличением количества замеров достоверность эксперимента возрастает, а доверительный интервал уменьшается. Таблица используется в том случае, когда о дисперсии исследуемой величины нельзя составить определенного мнения. Если же на основании априорных сведений или предварительных опытов (среднее квадратичное отклонение), известно, то по формуле случайной выборочной ошибки, равной половине длины доверительного интервала
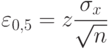 |
( 1.13) |
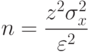 |
( 1.14) |
Точность и надежность оценки выборочных характеристик не следует смешивать с точностью исследования, которую часто вычисляют по такой формуле:
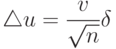 |
( 1.15) |
 — коэффициент вариации выборочного наблюдения, % (в случае оценки точности для сельскохозяйственных машин и процессов считается достаточным, если
— коэффициент вариации выборочного наблюдения, % (в случае оценки точности для сельскохозяйственных машин и процессов считается достаточным, если 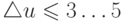 %.
%.
Кроме установления доверительных интервалов, задачи оценки случайных величин включают анализ законов распределения изучаемых величин, проверку принадлежности двух выборок к одной генеральной совокупности, сравнение средних дисперсий для различных выборок и др.
Рабочим инструментом статистического анализа при решении отмеченных задач оценки являются статистические гипотезы . Статистическими гипотезами именуются суждения, применяемые при различных видах анализа, касающихся, по существу, выяснения свойств некоторой генеральной совокупности случайных величин. Гипотеза в статистике трактуется как предположение о распределении случайных величин.
Гипотеза, отклонения от которой приписываются данному случаю, называется нулевой и обозначается 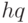 . Альтернативная или противоположная гипотеза называется конкурирующей и обозначается
. Альтернативная или противоположная гипотеза называется конкурирующей и обозначается  . Гипотезы проверяют при помощи специально подобранной случайной величины, распределение которой известно или может быть установлено при малом объеме выборки.
. Гипотезы проверяют при помощи специально подобранной случайной величины, распределение которой известно или может быть установлено при малом объеме выборки.
