НОУ ИНТУИТ | Параллельное программирование. Лекция 5: Параллельные методы расчета транспортной сети

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 1216 / 120 | Оценка: 4.73 / 4.45 | Длительность: 18:17:00

ISBN: 978-5-94774-546-7

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 13 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Начнем движение по ребрам из данной вершины. Для этого будем исключать из (5.12) одно из уравнений, а оставшуюся систему будем решать совместно с не вошедшими в (5.12) уравнениями:

y₃ = 0, y₄ = 0, y₅ = 0, y₆ = 0, y₉ = 0, y₁₂ = 0. (5.13)

При этом надо учесть, что могут формироваться ранее исследованные комбинации нулей. (Комбинации нулей удобно метить индексным кодом, который следует запоминать для исключения повторного анализа.)

Положим в (5.13) y₃ = 0 вместо y₁ = 0. Последняя строка матрицы A станет нулевой.

Замена y₁ = 0 уравнением y₄ = 0 приводит к системе

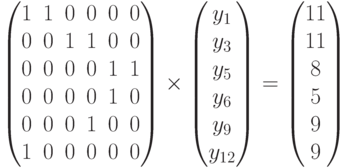
$\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_1\\y_3\\y_5\\y_6\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}$

Решаем с помощью подстановок, находим Y₁ = (2, 0, 9, 0, 2, 9, 0, 0, 3, 0, 0, 5). Т.к. Z(Y₁) = 127 > 119, найденную вершину отвергаем.

Примечание. Нам вновь не пришлось воспользоваться схемой Гаусса. По-видимому, вид уравнений и вхождение каждой переменной не более чем в два уравнения позволяют довольствоваться простой подстановкой. Ниже мы исследуем это подробнее.

Переходим к другому ребру, заменяя в (5.12) уравнение y₂ = 0 уравнениями из (5.13).

Замена y₃ = 0 вместо y₂ = 0 приводит к тому, что последняя строка матрицы A становится нулевой.

Замена y₄ = 0 вместо y₂ = 0 приводит к системе уравнений

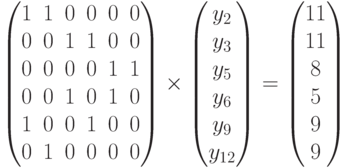
$\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_2\\y_3\\y_5\\y_6\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}$

Находим с помощью подстановок Y₁ = (0, 2, 9, 0, 4, 7, 0, 0, 1, 0, 0, 7). Т.к. Z(Y₁) = 127 > 119, найденную вершину отвергаем и переходим к анализу следующего ребра.

Замена y₃ = 0 вместо y₇ = 0 приводит к тому, что в первом уравнении (9.25) не выполняется условие по ограничению y₄ (y₄ = 7).

Замена y₄ = 0 вместо y₇ = 0 приводит к тому, что в первом же уравнении (9.25) не выполняется условие по ограничению y₃ (y₃ = 9).

Замена y₅ = 0 вместо y₇ = 0 приводит к системе

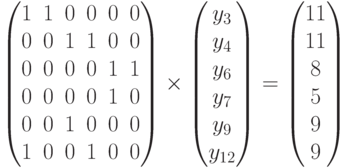
$\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_6\\y_7\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}$

Находим Y₁ = (0, 0, 7, 4, 0, 9, 2, 0, 5, 0, 0, 3). Однако Z(Y₁) = 129 > 119.

Переходим к анализу следующего ребра, поочередно заменяя уравнениями из (5.13) уравнение y₈ = 0 из (5.11).

Замена y₃ = 0 вместо y₈ = 0 приводит к образованию последней нулевой строки матрицы A.

Замена y₄ = 0 вместо y₈ = 0 приводит к тому, что в первом уравнении не выполняется условие по ограничению y₃ (y₃ = 9).

Замена y₅ = 0 вместо y₈ = 0 приводит к системе

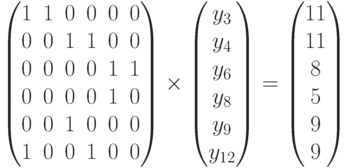
$\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_6\\y_8\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}$

Находим Y₁ = (0, 0, 9, 2, 0, 9, 0, 2, 5, 0, 0, 3). Т.к. Z(Y₁) = 141 > 119, найденную вершину отвергаем.

Переходим к анализу следующего ребра, поочередно заменяя уравнениями из (5.13) уравнение y₁₀ = 0 из (5.11).

Замена y₃ = 0 вместо y₁₀ = 0 приводит к тому, что в первом уравнении (5.11) не выполняется условие по ограничению y₄ (y₄ = 7).

Замена y₄ = 0 вместо y₁₀ = 0 приводит к тому, в первом же уравнении (5.11) не выполняется условие по ограничению y₃ (y₃ = 9).

Замена y₅ = 0 вместо y₁₀ = 0 приводит к тому, что во втором уравнении (5.11) не выполняется условие по ограничению y₆ (y₆= 9).

Замена y₆ = 0 вместо y₁₀ = 0 приводит к тому, что во втором же уравнении (5.11) не выполняется условие по ограничению y₅ (y₅ = 5).

Замена y₉ = 0 вместо y₁₀ = 0 приводит к системе

$\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_{10}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}$

Находим Y₁ = (0, 0, 9, 2, 5, 6, 0, 0, 0, 3, 0, 5). Т.к. Z(Y₁) = 104 < 119, "перемещаемся" в найденную вершину с меньшим значением целевой функции.

Новая вершина характеризуется системой уравнений

y₁ = 0, y₂ = 0, y₇ = 0, y₈ = 0, y₉ = 0, y₁₁ = 0. (5.14)

Перепишем систему (5.11), выделив "отсутствующие" столбцы, вследствие (5.14):

$\begin{equation} \setcounter{MaxMatrixCols}{20} \begin{pmatrix} \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}1 & 1 & 1 & 0 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & 0 & 1 & 1 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}0 & 0 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & 0 & 0 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}1 & 1 & \colorbox[gray]{0.8}1 & 1 \\ \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}0 & 0 & 0 & 1 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}1 & 0 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}1 & 0 & 0 & 0 & 1 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 1 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 1 & 0 & 0 & 0 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & \colorbox[gray]{0.8}1 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_1\\y_2\\y_3\\y_4\\y_5\\y_6\\y_7\\y_8\\y_9\\y_{10}\\y_{11}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

( 5.15)

После исключения одного из уравнений (5.14) оставшаяся система (5.15), (5.14) будет решаться совместно с одним из уравнений

y₃ = 0, y₄ = 0, y₅ = 0, y₆ = 0, y₁₀ = 0, y₁₂ = 0 (5.16)

Замена y₁ = 0 на y₃ = 0 приводит к появлению (последней) нулевой строки матрицы A.

Замена y₄ = 0 вместо y₁ = 0 приводит к системе

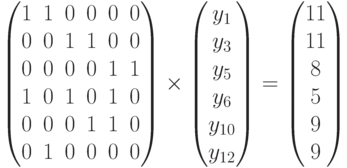
$\begin{equation*} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_1\\y_3\\y_5\\y_6\\y_{10}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation*}$

Отсюда Y₁ = (2, 0, 9, 0, 3, 8, 0, 0, 0, 1, 0, 7). Т.к. Z(Y₁) = 114 > 104, исследуем следующее ребро, исключив в системе (5.14) уравнение y₂ = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y₄ = 0 вместо y₂ = 0 приводит к системе

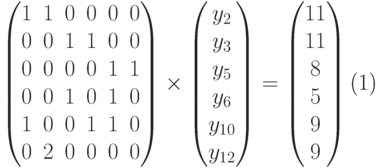
$\begin{equation} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 2 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_2\\y_3\\y_5\\y_6\\y_{10}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

Находим Y₁ = (0, 2, 9, 0, 5, 6, 0, 0, 0, 1, 0, 7). Т.к. Z(Y₁) = 114 > 104, исследуем следующее ребро, исключив в системе (5.14) уравнение y₇ = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y₃ = 0 вместо y₇ = 0 приводит к тому, что в первом уравнении (9.29) не выполняется условие по ограничению y₄ (y₄ = 7).

Замена y₄ = 0 вместо y₇ = 0 приводит к тому, что в первом же уравнении (9.29) не выполняется условие по ограничению y₃ (y₃= 9).

Замена y₅ = 0 вместо y₇ = 0 приводит к формированию нулевой (четвертой) строки матрицы A.

Замена y₆ = 0 вместо y₇ = 0 приводит к формированию нулевой (пятой) строки матрицы A.

Замена y₁₀ = 0 вместо y₇ = 0 приводит к тому, что в третьем уравнении (5.15) не выполняется условие по ограничению y₁₂ (y₁₂ = 7).

Замена y₁₂ = 0 вместо y₇ = 0 приводит к системе

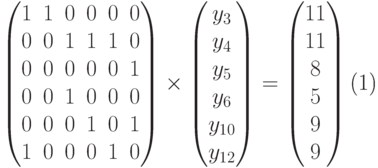
$\begin{equation} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_{10}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

Находим Y₁ = (0, 0, 4, 7, 5, 1, 5, 0, 0, 8, 0, 0). Т.к. Z(Y₁) = 104 и это не меньше уже полученной оценки, исследуем следующее ребро, исключив в системе (5.14) уравнение y₈ = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y₃ = 0 вместо y₈ = 0 приводит к образованию нулевой (шестой) строки матрицы A.

Замена y₄ = 0 вместо y₈ = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y₃ (y₃ = 9).

Замена y₅ = 0 вместо y₈ = 0 приводит к образованию нулевой (четвертой) строки матрицы A.

Замена y₆ = 0 вместо y₈ = 0 приводит к тому, что в пятом уравнении (5.15) не выполняется условие по ограничению y₁₀ (y₁₀= 8).

Замена y₁₀ = 0 вместо y₈ = 0 приводит к тому, что в третьем уравнении (5.15) не выполняется условие по ограничению y₁₂ (y₁₂ = 7).

Замена y₁₂ = 0 вместо y₈ = 0 приводит к системе

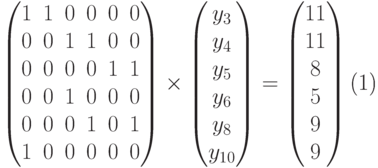
$\begin{equation} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_{8}\\y_{10} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

Ее решение Y₁ = (0, 0, 9, 2, 5, 1, 0, 5, 0, 8, 0, 0) определяет значение Z(Y₁) = 134 > 104. Продолжаем перебор по следующему ребру.

Замена y₃ = 0 вместо y₉ = 0 приводит к образованию нулевой (шестой) строки матрицы A.

Замена y₄ = 0 вместо y₉ = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y₃ (y₃ = 9).

Замена y₅ = 0 вместо y₉ = 0 приводит к тому, что во втором уравнении (5.15) не выполняется условие по ограничению y₆ (y₆= 9).

Замена y₆ = 0 вместо y₉ = 0 приводит к тому, что во втором же уравнении (5.15) не выполняется условие по ограничению y₅ (y₅ = 5).

Замена y₁₀ = 0 вместо y₉ = 0 приводит к системе

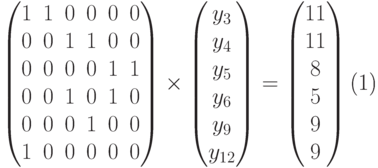
$\begin{equation} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_{9}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

Ее решение Y₁ = (0, 0, 9, 2, 2, 9, 0, 0, 3, 0, 0, 5) определяет значение Z(Y₁) = 119 > 104.

Приступаем к анализу следующего ребра, исключая в (5.14) уравнение y₁₁ = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y₃ = 0 вместо y₁₁ = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y₄ (y₄ = 7).

Замена y₄ = 0 вместо y₁₁ = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y₃ (y₃ = 9).

Замена y₅ = 0 вместо y₁₁ = 0 приводит к тому, что во втором уравнении (5.15) не выполняется условие по ограничению y₆ (y₆ = 9).

Замена y₆ = 0 вместо y₁₁ = 0 приводит к тому, что во втором же уравнении (5.15) не выполняется условие по ограничению y₅ (y₅ = 5).

Замена y₁₀ = 0 вместо y₁₁ = 0 приводит к системе

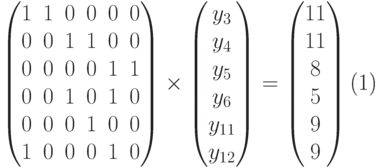$\begin{equation} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_{11}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

( 5.17)

Система не имеет решения, т.к. ранг матрицы системы не равен рангу расширенной матрицы.

Примечание. В несложном примере это легко обнаружить: вторая строка матрицы равна сумме четвертой и пятой строк, что противоречит соотношению между соответствующими свободными членами, 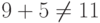$9 + 5 \ne 11$ . По-видимому, это говорит в пользу применения схемы Гаусса. В противном случае мы должны контролировать последовательно получаемые решения на удовлетворение тем соотношениям, которые в его получении не участвовали. Так, из четвертого и пятого уравнений имеем y₅ = 5, y₆ = 9. Но в соответствии со вторым уравнением y₅ + y₆ = 11. В то же время, совершая подстановку во второе уравнение, мы получаем нулевую левую часть, т.е. нулевую строку матрицы A, что опять говорит в пользу подстановок!

Замена y₁₂ = 0 вместо y₁₁ = 0 приводит к системе

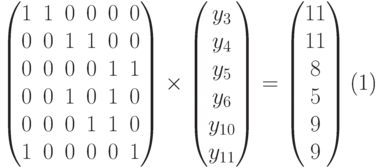
$\begin{equation} \begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_{10}\\y_{11} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation}$

Ее решение Y₁ = (0, 0, 4, 7, 5, 6, 0, 0, 0, 3, 5, 0) определяет значение целевой функции Z(Y₁) = 89 < 104.

Полагаем Y₀ := Y₁. Теперь мы должны перемещаться по ребрам из вновь найденной вершины в поисках вершины с еще меньшим значением целевой функции. Придется перебрать до 6 x 6 = 36 вариантов такого перемещения. Однако, достигнув ответа задачи в [15], положимся на его правильность и прекратим рассмотрение примера.

Дальше >>

Авторизоваться

Параллельное программирование

Лекция 5: Параллельные методы расчета транспортной сети

Вопросы и ответы