Интернет-Университет Суперкомпьютерных Технологий:

Параллельное программирование
[+]
Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 1216 / 120 | Оценка: 4.73 / 4.45 | Длительность: 18:17:00
ISBN: 978-5-94774-546-7
Темы: Программирование, Суперкомпьютерные технологии
Специальности: Программист
Теги: beta, SPMD, spmd-технология, алгоритмы, анализ, базы данных, вычисления, головной процессор, задача синхронизации, информационный граф, исследования, критический интервал, поиск, последний элемент списка, потоки, программирование, процедуры, процессоры, радио, расширенная матрица, серверы, сложность, стек процесса, транзитивные связи, указатели, элементы

Лекция 5: Параллельные методы расчета транспортной сети

A
|
версия для печати
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

Для нахождения других значений переменных необходимо решить систему уравнений на основе (5.8), после исключения нулевых столбцов

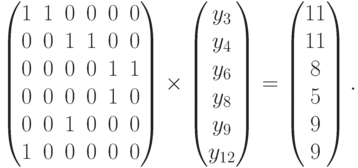
\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_6\\y_8\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\ 11\\ 8\\ 5\\ 9\\ 9 \end{pmatrix}.

Найдем все строки матрицы A, содержащие не более одного единичного элемента. Это строки, определяющие компоненты решения y3 = 9, y6 = 9, y9 = 5.

Выполним подстановку, последовательно находя в столбцах найденных переменных единицы (не более одной) и корректируя правые части вычитанием найденных значений. Строки и столбцы, соответствующие найденным значениям переменных, исключаем из матрицы A.

Такой прием подстановки можно повторять до исчерпания уравнений, содержащих в левой части единственную переменную.

В нашем примере после подстановки найденных значений в уравнения 1, 2 и 3 получаем систему

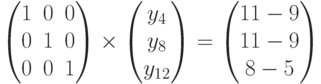
\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} y_4\\y_8\\y_{12} \end{pmatrix} = \begin{pmatrix} 11-9\\ 11-9\\ 8-5 \end{pmatrix}
В ней все уравнения имеют единственную переменную. Они определяют решение y4 = 2, y8 = 2, y12 = 3.

Таким образом, нам не пришлось пока воспользоваться методом Гаусса, но мы нашли допустимое решение Y0 = (0, 0, 9, 2, 0, 9, 0, 2, 5, 0, 0, 3), для которого выполняются ограничения задачи. Вектор Y0 определяет некоторую вершину многогранника допустимых решений, со значением целевой функции Z(Y0) = 141.

Примем следующий план решения, соответствующий рассмотренному ранее плану параллельного решения задач линейного программирования.

Для перебора всех смежных вершин необходимо в комбинации нулей, определивших вершину Y0, поочередно исключать одно значение yr = 0 (это определит одно из исходящих ребер) и оставшуюся систему решать совместно поочередно со всеми другими уравнениями вида ys = 0, не входящими в комбинацию нулей. Этим мы будем совершать перемещение в смежные вершины. Находя значение Z для каждого такого решения Y1 там, где оно существует, можно найти вершину с меньшим значением целевой функции. "Перебравшись" в эту вершину (приняв ее за Y0 ), мы можем продолжить анализ смежных ей вершин и т.д. Решение задачи найдено в том случае, если после перебора всех смежных вершин не отыскивается вершина с меньшим значением целевой функции.

Продолжим рассмотрение примера.

Итак, (5.8) — исходный вид системы уравнений, (5.9) — комбинация нулей ("отсутствующие" столбцы в (5.7) выделены), (5.8) и (5.9) определяют вершину Y0.

Исключим из (5.9) уравнение y1 = 0, а оставшуюся систему, с учетом остальных нулей из комбинации (5.9), будем решать совместно с уравнениями

y3 = 0, y4 = 0, y6 = 0, y8 = 0, y9 = 0, y12 = 0. (5.10)

Значит, в (5.8) положим первоначально y3 = 0 вместо y1 = 0. Левая часть шестого уравнения (последняя строка матрицы А) обратилась в нуль.

Положим y4 = 0 вместо y1 = 0. Получим систему

\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ \end{pmatrix} \times \begin{pmatrix} y_1\\y_3\\y_6\\y_8\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}
Из нее, как и ранее, за два шага подстановки находим y3 = 9, y6 = 9, y9 = 5, а затем — y1 = 2, y8 = 2, y12 = 3.

Таким образом, найдено новое допустимое решение Y1 = (2, 0, 9, 0, 0, 9, 0, 2, 5, 0, 0, 3). Однако Z(Y1) =149 > 141. Найденную вершину отвергаем. Вместе с тем, т.к. мы нашли вершину "на другом конце" анализируемого ребра, то и анализ этого ребра прекращаем.

Приступаем к анализу следующего ребра, исключив из (5.9) уравнение y2 = 0. Оставшуюся систему, с учетом остальных нулей из (5.9), будем решать совместно с теми же уравнениями (5.10).

Положим в (5.8) y3 = 0 вместо y2 = 0. Последняя строка матрицы A стала нулевой.

Замена y4 = 0 вместо y2 = 0 приводит к системе

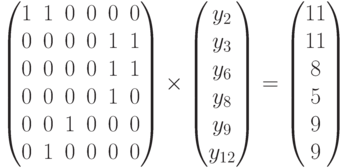
\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ \end{pmatrix} \times \begin{pmatrix} y_2\\y_3\\y_6\\y_8\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}
На ее основе находим новый вектор — допустимое решение Y1 = (0, 2, 9, 0, 0, 9, 0, 2, 5, 0, 0, 3). Однако Z(Y1) = 151 > 141. Найденную вершину также отвергаем. Ребро исследовано полностью.

Исключим из (5.9) уравнение y5 = 0, а оставшуюся систему, с учетом остальных нулей из (5.9), будем решать совместно с теми же уравнениями (5.10).

Положим в (5.8) y3 = 0 вместо y5 = 0. Последняя строка матрицы A обратится в нуль.

Положим y4 = 0 вместо y5 = 0. В первом уравнении не выполняется ограничение по y3 (y3 = 9).

Положим y6 = 0 вместо y5 = 0. Пятая строка A обратилась в нулевую.

Положим y8 = 0 вместо y5 = 0. Получим систему уравнений

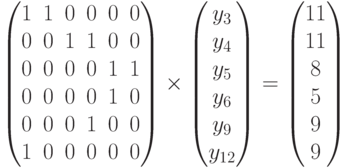
\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}
Находим y3 = 9, y6 = 9 и после подстановки — y4 = 2, y5 = 2. Вновь выполняем подстановку, находим y9 = 3, и после следующей подстановки y12 = 5.

Итак, получена вершина Y1 = (0, 0, 9, 2, 2, 9, 0, 0, 3, 0, 0, 5). Т.к. Z(Y1) = 119 < 141, полагаем Y0 := Y1 и начинаем пробу возможных перемещений вдоль ребер из найденной вершины многогранника решений в вершину с меньшим значением целевой функции:

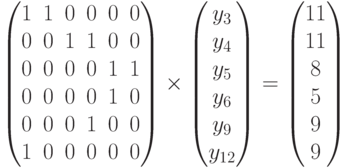
\begin{pmatrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_3\\y_4\\y_5\\y_6\\y_9\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix}
Запишем вновь аналогично (5.8) и (5.9) систему уравнений, решением которой является вершина Y0, отметив в ней "отсутствующие" столбцы:
\begin{equation} \setcounter{MaxMatrixCols}{20} \begin{pmatrix} \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}1 & 1 & 1 & 0 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & 0 & 1 & 1 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}1 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & 0 & 0 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 1 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}1 & 1 \\ \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}0 & 0 & 0 & 1 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 1 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}1 & 0 & 0 & 0 & 1 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 0 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}0 & 0 \\ \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}0 & 1 & 0 & 0 & 0 & \colorbox[gray]{0.8}1 & \colorbox[gray]{0.8}0 & 0 & \colorbox[gray]{0.8}0 & \colorbox[gray]{0.8}1 & 0 \\ \end{pmatrix} \times \begin{pmatrix} y_1\\y_2\\y_3\\y_4\\y_5\\y_6\\y_7\\y_8\\y_9\\y_{10}\\y_{11}\\y_{12} \end{pmatrix} = \begin{pmatrix} 11\\11\\8\\5\\9\\9 \end{pmatrix} \end{equation} ( 5.11)
Находим

y1 = 0, y2 = 0, y7 = 0, y8 = 0, y10 = 0, y11 = 0. (5.12)

Дальше >>
< Лекция 4 || Лекция 5: 123456789 || Лекция 6 >

Вопросы и ответы

вопросов: 0