Сетевые технологии параллельного программирования

Организация параллельного решения задачи в локальной сети

Распараллеливание метода "сеток" с очевидностью адекватно второму способу распараллеливания, что и должно определить направление поиска. То есть можно с уверенностью заявить, что распределение узлов сетки между процессорами ВС (распараллеливание по информации), ЭВМ вычислительного комплекса или рабочих станций сети является эффективным способом параллельного решения системы дифференциальных уравнений в конечных разностях.

В "Параллельные технологии решения информационно-логических задач" рассматривался пример решения уравнения в частных производных. Далее на этом примере будут показаны схемы возможной реализации метода сеток в ЛВС.

По рис. 1.12 из курса "Архитектура параллельных вычислительных систем" мы можем полностью представить различные планы параллельного решения рассмотренной задачи.

Метод матричных вычислений характерен для матричных вычислительных систем. В таких системах организуются "быстрые" связи между процессорами в соответствии с преимущественными направлениями обменов информацией. Обычно это связи по строке и по столбцу с соединением "последнего с первым". Матрица процессоров "накладывается" на множество узлов сетки, воспроизводящее такую же матрицу, и узлы обрабатываются. Матрица процессоров циклически обходит матрицы узлов сетки.

Другая стратегия распределения узлов между процессорами может быть основана на делении области задания функции между процессорами. Т.е. вся область D на рис. 1.12 из курса "Архитектура параллельных вычислительных систем" может быть разделена поровну между процессорами ВС или станциями сети.

Третья стратегия может предусматривать нумерацию процессоров, превращение многомерного (в примере — двумерного) массива узлов сетки в одномерный линейный и назначение каждого узла на процессор с номером, равным остатку от деления его номера на число используемых процессоров. Эта стратегия, в наибольшей степени обеспечивающая инвариантность программы счета относительно числа узлов и числа используемых процессоров, соответствует рассмотренной ранее SPMD-технологии.

Равноправие процессоров (симметричность) делают целесообразным использование шинной архитектуры ЛВС. (Отметим, что на ранней стадии построения вычислительных комплексов применялась именно шинная архитектура, как наиболее простая и естественная. То же можно отметить и относительно многих современных и перспективных мультимикропроцессорных систем.) Распространенным стандартом такой архитектуры, обусловившим разработку широкой номенклатуры аппаратных средств, является сеть ETHERNET. Параллельный вычислительный процесс должен воспроизводить технологию SPMD, основанную на применении способа распараллеливания по информации.

Тогда организация параллельной обработки информации и схема вычислений должна быть следующей.

1. Исследуется задача и выделяется основной массив данных (одномерный или многомерный), обработку которого целесообразно распределить между станциями ЛВС, — опорный массив.
2. Формируется план распределения элементов опорного массива для обработки станциями сети. Разнообразие таких планов порождает и разнообразие возможных способов переадресации. Например, весь опорный массив может быть поровну (со следующими подряд элементами) поделен между станциями. Такой способ может применяться в случае, если длина массива не изменяется динамически. Более универсален способ распределения элементов опорного массива, когда после "расчета по n " каждый из них оказывается закрепленным за станцией с тем же номером. Это в точности соответствует технологии SPMD и поддержано системой команд. Такое распределение допускает динамическое изменение длин массивов (поддерживает динамический тип данных), что крайне важно при обработке баз знаний.
3. Составляется единственная для всех станций (предполагается их программная совместимость), универсальная программа циклической обработки элементов опорного массива, закрепленных за одной станцией. Программа должна содержать критический интервал обмена данными между станциями в необходимых (по алгоритму) направлениях. При этом запрос с последующим ожиданием данных (принцип редукционных вычислительных систем) должен отсутствовать, данные должны только отправляться. Это значит, что программы должны "уметь" ждать необходимые для себя данные. Поэтому становится целесообразным воспроизведение принципа data flow с помощью "почтовых ящиков".
4. Составляется программа ввода, визуализации и управления вычислительным процессом для станции (персонального компьютера), который назначается мониторным.
5. Задача решается в диалоговом режиме. Дело в том, что при большом времени собственно решения вмешательство пользователя (оператора) может быть не только неизбежным, но и желательным. Например, нахождение всех экстремумов функции можно автоматизировать следующим образом: разделить область задания функции между компьютерами и поручить им полностью исследовать свои подобласти; затем заставить их совместно исследовать полученные результаты и выделить глобальные экстремумы и др. Вторая задача может оказаться существенно сложнее. В то же время оператором она может быть решена значительно проще при достаточной визуализации. Принятое им решение может быть немедленно использовано при последующем автоматическом решении этой или другой задачи.

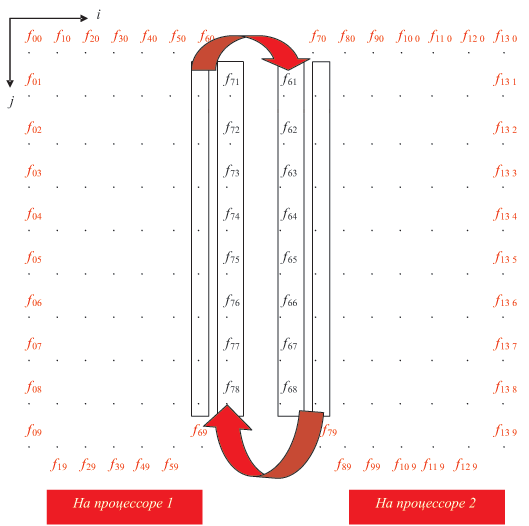
Рассмотрим конкретный возможный план решения рассмотренной выше задачи методом "сеток". Для простоты положим число используемых процессоров равным 2. В основу плана положим способ разделения области D между процессорами поровну. Зафиксируем h_x = h_y = h, определив тем самым количество узлов сетки в каждой строке и в каждом столбце. На рисунке 3.6 отражены выбранные количества узлов в строках и столбцах. Первая и последняя строка, как и первый и последний столбец, соответствуют узлам, в которых заданы граничные значения функции-решения.

Рис. 3.6. Распределение данных между двумя процессорами для решения задачи методом "сеток"

Область D₁, обрабатываемая процессором 1, определяется границами индекса i и координаты x:

Область D₂, обрабатываемая процессором 2, определяется границами индекса i и координаты x:

По второй координате 0 <= y <=t (m - 1)h = B.

На рисунке показана передача промежуточных значений узлов процессором процессору для счета узлов, использующих эти значения. Такая передача может осуществляться либо непосредственно после нахождения очередного приближения значения функции в узле, либо после очередной итерации — для всех необходимых значений сразу. Второй способ может значительно сократить время выполнения обмена, хотя задерживает использование узлов.

Важен выбор способа нахождения начального значения функции — решения в узлах. Этот выбор влияет на скорость сходимости решения.

В соответствии с граничными условиями

f_i0 = f₁(ih,0) i = 0, ..., n - 1,

f_i,m-1 = f₂(ih,(m-1)h=B) i = 0, ..., n - 1,

f_0j = f₃(0,jh) j = 0, ..., m - 1,

f_n-1,j = f₄((n-1)h=A,j) j = 0, ..., m - 1.

Нулевое приближение значений f_ij может быть рассчитано по формулам интерполяции с усреднением:

для всех 0 < i < A, 0 < j < B.

Итерационная формула имеет общий вид f_ij = F(f_i-1,j, f_i+1,j, f_i,j-1, f_i,j+1).