НОУ ИНТУИТ | Параллельное программирование. Лекция 2: Применение SPMD-технологии при построении сетевых баз данных с циркулирующей информацией

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 1223 / 124 | Оценка: 4.73 / 4.45 | Длительность: 18:17:00

ISBN: 978-5-94774-546-7

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 13 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Эффективность и технические требования

В общем случае, при вхождении сервера в состав ЛВС и при разбиении БД на m сегментов, при котором m > n ( n — число рабочих станций), вероятность нахождения сегмента на одной из РС в процессе ротации равна $\frac{n}{m}$ . Вероятность нахождения сегмента на конкретной РС равна $\frac{1}{m}$ .

Схема на рис. 2.3 соответствует случаю m = n.

Тогда среднее время T_ож ожидания нужного сегмента, то есть возможного начала обращения к нужному сегменту на той РС, которая выработала запрос, находится на основе вероятности того, что он поступит через один такт, через два такта и т.д. Максимальное число учитываемых тактов равно m - 1:

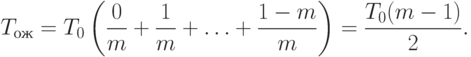$\begin{align*} T_{ож} = T_0 \left(\frac{0}{m}+\frac{1}{m}+ \ldots + \frac{1-m}{m}\right) = \frac{T_0(m-1)}{2}. \notag \end{align*}$

( 2.1)

Тогда полное время обслуживания запроса в ротационной БД находится следующим образом:

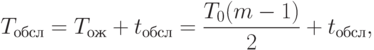$\begin{align*} T_{обсл} = T_{ож} + t_{обсл} = \frac{T_0(m-1)}{2} + t_{обсл}, \notag \end{align*}$

( 2.2)

где t_обсл — время выполнения запроса с помощью СУБД.

Сравним это полное время обслуживания со средним временем обслуживания T^*_обсл "традиционной" БД, реализованной на сервере. Напомним, что при обслуживании такой БД многоканальная система массового обслуживания, где множество рабочих станций обеспечивают массовый доступ, реально, с помощью одноканальной СУБД, на этапе обслуживания потока заявок преобразуется в одноканальную систему массового обслуживания с неограниченной очередью.

Допустив, что время выполнения запроса с помощью СУБД в данном случае совпадает с тем же временем в ротационной БД (ротация не предполагает каких-либо принципиальных изменений "традиционных", известных, широко применяемых СУБД), получим:

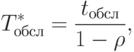$\begin{align*} T^*_{\text{обсл}} = \frac{t_{\text{обсл}}}{1-\rho}, \notag \end{align*}$

( 2.3)

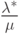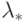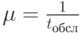где $\rho$ — известное отношение $\frac{\lambda^*}{\mu}$ , а $\lambda _{*}$ — суммарная интенсивность потока запросов со всех рабочих станций ЛВС, $\mu$ — интенсивность обслуживания, $\mu = \frac{1}{t_{\text{обсл}}}$ .

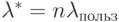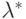Уточним, что $\lambda ^{*} = n\lambda _{польз}$ , где $\lambda _{польз}$ — интенсивность потока запросов с одной РС при данной организации БД. Однако здесь мы пренебрегли временем передачи сообщений в ЛВС, учитывая существенный характер ограничений другого рода. А именно, суммарная интенсивность $\lambda ^{*}$ потока запросов в системе должна быть ограничена значением, обеспечивая соотношение $\rho < 1$ . 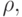Полное время обслуживания T^*_обсл значительно возрастает при значениях $\rho,$ близких единице:

$T^{*}_{обсл} \to \infty$ ,

$\rho \to 1$ .

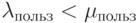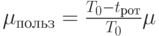В ротационной базе данных каждая РС независимо от других реализует одноканальную систему массового обслуживания с неограниченной очередью, где, несомненно, тоже должно выполняться соответствующее ограничение $\lambda _{польз} <\mu _{польз}$ , где $\lambda _{польз}$ — интенсивность запросов пользователя с одной РС, $\mu _{польз}$ — интенсивность обслуживания запросов пользователя с одной РС, $\mu_{\text{польз}} = \frac{T_0 - t_{\text{рот}}}{T_0}\mu$ Однако пользователь полностью управляет своими запросами, и случайный характер их поступления изучать нецелесообразно. Дисциплинированный пользователь формирует свои запросы последовательно, в диалоговом режиме, и не формирует новых запросов, не дождавшись ответа на предыдущие. Тогда приблизительно можно считать, что интенсивность потока запросов пользователя ограничена некоторыми возможностями системы, а именно

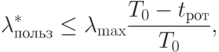$\begin{align*} \lambda^*_{\text{польз}} \le \lambda_{\max} \frac{T_0 - t_{\text{рот}}}{T_0}, \notag \end{align*}$

( 2.4)

где $\lambda _{max}$ — некоторая максимально возможная интенсивность потока запросов, последовательно (по мере выполнения) формируемых пользователем в том случае, если доступ к сегментам базы данных, находящимся в памяти его РС, не ограничен ротацией, т.е. t_рот = 0.

Таким образом, исследуя вопрос о целесообразности построения ротационной БД, необходимо изучить практические возможности обеспечения таких характеристик ЛВС, их аппаратных и программных средств, при которых выполняется соотношение

$\begin{align*} T_{\text{обсл}} < T^*_{\text{обсл}}, \notag \end{align*}$

или

$\begin{align*} \frac{T_0(m-1)}{2} + t_{\text{обсл}} < \frac{t_{\text{обсл}}}{1 - \rho} \notag \end{align*}$

( 2.5)

где

$\begin{align*} \rho = \frac{n\lambda_{\text{польз}}}{\mu} \end{align*}$

Напоминаем, что здесь

T₀ — время (длина) такта системы,

m — число сегментов БД,

n — число рабочих станций ЛВС,

t_обсл — время выполнения одного запроса СУБД (характеристика используемой системы управления базой данных),

$\lambda _{польз}$ — интенсивность потока запросов одного пользователя,

$\mu$ — интенсивность обслуживания запросов данной СУБД.

Однако выражение (2.5) получено в предположении, что заявка на обслуживание, поступившая от конкретной РС к некоторому сегменту s_i, не претерпевает какого-либо влияния возможных, в достаточно близкое время, заявок, пришедших к этому же сегменту от других РС "на пути следования" сегмента к данной РС. А именно, за предполагаемое среднее время T_ож требуемый сегмент может быть "перехвачен" другой РС, "предшествующей" ожидающей. При значительной интенсивности $\lambda$ заявок такой возможностью нельзя пренебречь.

Предположим не более чем однократную возможность такого "перехвата".

Тогда, считая, что поток заявок к БД простейший (пуассоновский, экспоненциальный), вероятность P_i того, что сегмент s_i без дополнительных помех на пути следования дойдет до данной РС, находится как

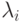$\begin{align*} P_i = \exp (-\lambda_i T_{\text{ож}}). \notag \end{align*}$

( 2.6)

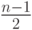Здесь $\lambda _{i}$ — суммарная интенсивность запросов к сегменту s_i за время T_ож от среднего числа $\frac{n-1}{2}$ других пользователей, находящихся "на пути следования" этого сегмента.

Если запросы ко всем сегментам равновероятны, то

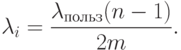$\begin{align*} \lambda_i = \frac{\lambda_{\text{польз}}(n - 1)}{2m}. \notag \end{align*}$

( 2.7)

Тогда

$\begin{align*} P_i = P = \exp (-\frac{\lambda_{\text{польз}}(n - 1)}{2m} T_{\text{ож}}). \notag \end{align*}$

( 2.8)

При однократном "перехвате" его вероятность считаем равной 1-P.

"Перехват" дополняет общее время выполнения заявки составляющей (1-P)t_обсл. Тогда окончательно среднее время обслуживания заявок в ротационной БД в рассматриваемом случае определяется как

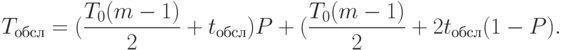$\begin{align*} T_{\text{обсл}} = (\frac{T_0(m-1)}{2}+t_{\text{обсл}})P+(\frac{{T_0}(m-1)}{2}+2t_{\text{обсл}}(1-P). \notag \end{align*}$

( 2.9)

Вместо выражения (2.5), с учетом (2.1), (2.8), (2.9), для обоснования ротации информации мы должны так подобрать параметры сети, сегментацию БД и временные параметры ротации, чтобы выполнялось (причем существенно!) соотношение

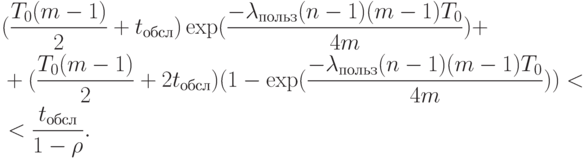$\begin{align*} &(\frac{T_0(m-1)}{2}+t_{\text{обсл}})\exp (\frac{-\lambda_{\text{польз}}(n - 1)(m - 1)T_0}{4m})+ \notag \\ &+ (\frac{{T_0}(m-1)}{2}+2t_{\text{обсл}})(1-\exp (\frac{-\lambda_{\text{польз}}(n - 1)(m - 1)T_0}{4m}))< \notag \\ &< \frac{t_{\text{обсл}}}{1-\rho}. \notag \end{align*}$

( 2.10)

Дальше >>

Авторизоваться

Параллельное программирование

Применение SPMD-технологии при построении сетевых баз данных с циркулирующей информацией

Эффективность и технические требования

Вопросы и ответы