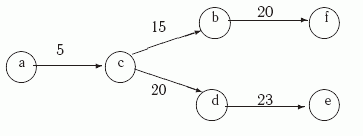
|
Это в лекции 3. |
Три алгоритма на графах
Задача о кратчайших путях из одного источника
Пусть G=(V,E) - ориентированный граф, для каждого ребра 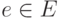 которого указана
его (неотрицательная) длина: c(e) >= 0. Тогда длина пути p=v1,v2, ... , vk+1
определяется как сумма длин ребер, входящих в этот путь:
которого указана
его (неотрицательная) длина: c(e) >= 0. Тогда длина пути p=v1,v2, ... , vk+1
определяется как сумма длин ребер, входящих в этот путь: 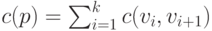 .
Если в G имеется путь из вершины a в вершину b, то имеется и такой путь минимальной длины.
Он называется кратчайшим путем из a в b. Конечно, в графе
может оказаться несколько
различных кратчайших путей из a в b.
.
Если в G имеется путь из вершины a в вершину b, то имеется и такой путь минимальной длины.
Он называется кратчайшим путем из a в b. Конечно, в графе
может оказаться несколько
различных кратчайших путей из a в b.
Естественно спросить, как узнать длину кратчайшего
пути из a в b и построить его? Лучшие известные на сегодняшний день алгоритмы,
отвечающие на этот вопрос,
решают, на самом деле, более общую задачу построения всех кратчайших путей
из одного источника: по вершине a найти длины кратчайших путей из a во все достижимые из
нее вершины и построить для каждой из таких вершин некоторый кратчайший путь из a.
Если для каждой вершины 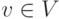 , достижимой из a, зафиксировать один кратчайший путь из a
в v, то получившийся граф будет представлять ориентированное дерево с корнем a (докажите это!).
Это дерево называется деревом кратчайших путей из a.
, достижимой из a, зафиксировать один кратчайший путь из a
в v, то получившийся граф будет представлять ориентированное дерево с корнем a (докажите это!).
Это дерево называется деревом кратчайших путей из a.
Мы рассмотрим алгоритм построения дерева кратчайших путей и определения их длин, предложенный в 1959г. Е. Дейкстрой. Его идея следующая: перед каждым этапом известно множество отмеченных вершин S, для которых кратчайшие пути найдены ранее; тогда на очередном этапе к нему добавляется вершина w, с самым коротким путем из a, проходящим по множеству S ; после этого пересчитываются длины кратчайших путей из a в оставшиеся вершины из V \ S с учетом новой вершины w. Длина текущего кратчайшего пути из a в v, проходящего по множеству S, заносится в ячейку D[v] массива D. В конце работы в этом массиве отыскиваются длины соответствующих кратчайших путей. Для определения дерева кратчайших путей служит массив ОТЕЦ, его элемент ОТЕЦ[v] содержит ссылку на вершину, из которой кратчайший путь приходит в v .
Алгоритм Дейкстры
Вход: G=(V,E) - ориентированный граф, c(u,v) >= 0 -длина ребра 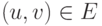 (если
(если  , то считаем, что
, то считаем, что 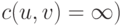 и исходная вершина
и исходная вершина 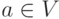 .
.
=== ИНИЦИАЛИЗАЦИЯ ===
1. S := {a}; ' отметить a
2. D[a] := 0; ' расстояние от a до a
3. ДЛЯ КАЖДОЙ v принадлежащей V, v != a ВЫПОЛНЯТЬ
4. {D[v] := c(a,v); ' расстояние от a до v через a
5. ЕСЛИ c(a,v) < бесконечности ТО ОТЕЦ[v]:= a ИНАЧЕ ОТЕЦ[v]:= - };
=== ОСНОВНОЙ ЦИКЛ ===
6. ПОКА V \ S не пусто ВЫПОЛНЯТЬ ' есть неотмеченные вершины
7. { выбрать неотмеченную вершину w с минимальным D[w];
8. S := S объединение с {w}; ' отметить w
9. ДЛЯ КАЖДОЙ (неотмеченной) u принадлежит V \ S ВЫПОЛНЯТЬ
10. ЕСЛИ D[u] > D[w] + c(w,u)
11. ТО { D[u] := D[w] + c(w,u);
12. ОТЕЦ[u]:= w}
13. }Пример 11.3.
Рассмотрим работу этого алгоритма на нагруженном графе G=(V={a, b, c, d, e, f}, E)
и выделенной вершине 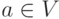 . Зададим длины ребер матрицей C= (cuv), где элемент cuv=c(u,v):
. Зададим длины ребер матрицей C= (cuv), где элемент cuv=c(u,v):
![\[\left( \begin{array}{crrrrrr}
&a& b& c & d & e & f \\
a &0 & 25& 5 & 30 & \infty & 75\\
b &12 & 0& \infty & \infty & 120 & 20\\
c &\infty & 15& 0 & 20 & 45 & 60\\
d &\infty & \infty& \infty & 0 & 23 & 20\\
e & \infty & \infty & 75 & 20 & 0 & 20\\
f & 40 & 15& 15 & 26 & \infty & 0
\end{array} \right) \]](/sites/default/files/tex_cache/d1a56d3913f80f422a60fed496cae224.png)
Поэтапную работу алгоритма Дейкстры удобно представлять в виде таблицы, строки которой соответствуют его этапам. Первый столбец - номер этапа, второй показывает изменение множества отмеченных вершин S, третий - вершину w, добавляемую к S на текущем шаге, четвертый - длину кратчайшего пути из a в w, затем идут столбцы со значениями элементов массивов D и ОТЕЦ.
Дерево кратчайших путей из вершины a задается массивом ОТЕЦ. Оно представлено на рис. 11.5.
Теорема 11.4. (о корректности алгоритма Дейкстры)
Алгоритм Дейкстры строит дерево кратчайших путей из вершины a во все достижимые из нее вершины и для каждой такой вершины v определяет длину D[v] кратчайшего пути в нее из a.
Доказательство Докажем по индукции, что после каждого этапа алгоритма выполнены следующие условия:
- для любой вершины
 величина D[v] равна длине кратчайшего пути из a в v ;
величина D[v] равна длине кратчайшего пути из a в v ; - для любой вершины
 величина D[v] равна длине кратчайшего пути из a в v, проходящего по множеству S ;
величина D[v] равна длине кратчайшего пути из a в v, проходящего по множеству S ; - для каждой вершины v дерева T, задаваемого массивом ОТЕЦ, длина пути из корня a в v равна D[v].
Эти три условия очевидно выполняются после инициализации в строках 1- 5.
Предположим теперь, что они выполнены перед началом k -го этапа.
Пусть w - вершина, добавляемая к S на k -ом этапе. По предположению, D[w] - длина кратчайшего пути из a в w, все вершины которого, кроме w, входят в S. Предположим, что
есть другой более короткий путь p из a в w. Зафиксируем на этом пути первую
вершину u, не входящую в S. По выбору p 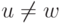 . Поэтому путь p разбивается
на две непустые части: путь p1 из a в u и путь p2 из u в w. Но по выбору w
мы имеем, что длина p1 >= D[u] >= D[w]. Так как длина p2 неотрицательна, то длина p >= D[w], т.е. этот путь не короче пути, представленного в дереве T. Таким образом, D[w] - это длина кратчайшего пути из a в w. Следовательно, условие (а) выполнено и после k -го этапа.
. Поэтому путь p разбивается
на две непустые части: путь p1 из a в u и путь p2 из u в w. Но по выбору w
мы имеем, что длина p1 >= D[u] >= D[w]. Так как длина p2 неотрицательна, то длина p >= D[w], т.е. этот путь не короче пути, представленного в дереве T. Таким образом, D[w] - это длина кратчайшего пути из a в w. Следовательно, условие (а) выполнено и после k -го этапа.
Рассмотрим теперь произвольную вершину  . Кратчайший путь p из a в u, проходящий по множеству
. Кратчайший путь p из a в u, проходящий по множеству 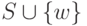 ,
либо не включает вершину w и в этом случае его длина равна D[u] и он имеется в текущем
дереве T, либо он проходит через w и составлен из кратчайшего пути из a в w через S, продолженного ребром (w,u). В последнем случае длина пути равна D[w] + c(w,u). Но в 10-ой строке алгоритма эти величины сравниваются и, если
путь через w короче, то его длина становится новым значениием D[u] (строка 11) и
он фиксируется в дереве T (строка 12). Следовательно, условия (б)
и (в) также выполнены после k -го этапа.
,
либо не включает вершину w и в этом случае его длина равна D[u] и он имеется в текущем
дереве T, либо он проходит через w и составлен из кратчайшего пути из a в w через S, продолженного ребром (w,u). В последнем случае длина пути равна D[w] + c(w,u). Но в 10-ой строке алгоритма эти величины сравниваются и, если
путь через w короче, то его длина становится новым значениием D[u] (строка 11) и
он фиксируется в дереве T (строка 12). Следовательно, условия (б)
и (в) также выполнены после k -го этапа.
Так как после завершения алгоритма S = V, то в завершающем дереве T
представлены кратчайшие пути из a во все достижимые из нее вершины,
а массив D содержит длины этих путей. Значение ![D[u]= \infty](/sites/default/files/tex_cache/d6d6844bf617078a96ba91421946f8de.png) указывает на то, что
вершина u не достижима из вершины a.
указывает на то, что
вершина u не достижима из вершины a.
Замечание о сложности. На каждом этапе (исполнении тела основного цикла в стр. 6 - 13) одна вершина добавляется во множество S. Поэтому таких этапов не более |V|.
Чтобы выбрать в массиве D вершину w с минимальным D[w] (стр. 7), требуется
не более |V| шагов. Перевычисление D[u] для каждой из вершин 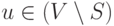 требует константного числа операций, поэтому весь цикл в стр. 9 - 12 потребует
не более c |V| шагов. Отсюда получаем, что для некоторой константы c
время выполнения алгоритма Дейкстры не превышает c |V|2. Поскольку размер любого представления исходного графа не меньше |V|, то алгоритм работает в квадратичное время (от размера входа).
требует константного числа операций, поэтому весь цикл в стр. 9 - 12 потребует
не более c |V| шагов. Отсюда получаем, что для некоторой константы c
время выполнения алгоритма Дейкстры не превышает c |V|2. Поскольку размер любого представления исходного графа не меньше |V|, то алгоритм работает в квадратичное время (от размера входа).