НОУ ИНТУИТ | Основы дискретной математики. Лекция 2: Индукция и комбинаторика

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Тверской государственный университет

Опубликован: 21.08.2007 | Доступ: свободный | Студентов: 3170 / 268 | Оценка: 4.08 / 3.92 | Длительность: 15:40:00

ISBN: 978-5-9556-0110-6

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Математик

|

Вам нравится? Нравится 37 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Метод математической индукции. Индукция по структуре объекта. Комбинаторика: число размещений, перестановок и сочетаний. Принцип включения и исключения

Метод математической индукции

Математическая индукция - это весьма общий метод, который позволяет доказывать утверждения, зависящие от целочисленных параметров. Его можно сформулировать следующим образом.

Пусть P(n) - это некоторое утверждение, зависящее от целочисленного параметра n. Пусть, во-первых, утверждение P(n₀) справедливо и пусть, во-вторых, для любого k >= n₀ из справедливости P(k) следует справедливость P(k+1). Тогда утверждение P(n) справедливо для всех n >= n₀.

Таким образом доказательство "по индукции" состоит из двух этапов.

Базис (или основание) индукции состоит в доказательстве утверждения P(n₀) для некоторого начального значения n₀ ( обычно n₀=1, но это не обязательно).
Шаг индукции состоит в предположении справедливости P(n) при n=k >= n₀ и доказательстве из этого предположения справедливости утверждения P(k+1) .

Рассмотрим несколько примеров применения метода математической индукции.

Пример 1. Доказать, что при n>= 1

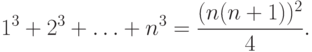
$1^3 +2^3 + \ldots + n^3 = \frac{(n(n+1))^2}{4}.$

Базис индукции. При n=1 имеем

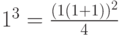$1^3=\frac{(1(1+1))^2}{4}$ .
Шаг индукции. Допустим, что при n=k

$1^3 +2^3 + \ldots + k^3 = \frac{(k(k+1))^2}{4}.$

Докажем тогда, что при n=k+1

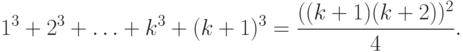
$1^3 +2^3 + \ldots + k^3 +(k+1)^3= \frac{((k+1)(k+2))^2}{4}.$

Действительно,

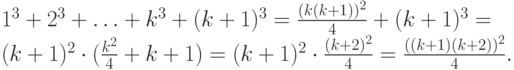
$1^3 +2^3 + \ldots + k^3 +(k+1)^3=\frac{(k(k+1))^2}{4} +(k+1)^3 =\\ (k+1)^2\cdot(\frac{k^2}{4}+k+1)= (k+1)^2\cdot \frac{(k+2)^2}{4}= \frac{((k+1)(k+2))^2}{4}.$

Таким образом, наше утверждение выполненопри всех n>= 1.

Пример 2. Доказать, что для любого $x > -1,\ x \ne 0$ , и натурального n>= 2 выполнено неравенство (1+x)ⁿ > 1 +nx (это неравенство называют неравенством Бернулли).

Базис индукции. При 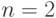, учитывая, что 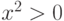, имеем (1+x)²=1 +2x +x² > 1+2x.
Шаг индукции. Допустим, что при n=k неравенство справедливо, т.е. (1+x)^k > 1 +kx. Покажем, что тогда оно выполнено и при n=k+1. Действительно, так как 1+x > 0, то умножив обе части на 1+x > 0, получим (1+x)^k(1+x)=(1+x)^k+1 > (1+kx)(1+x)=1+ (k+1)x +kx²> 1+(k+1)x, что и требовалось.

В обычном понимании слово "индукция" означает переход от частных случаев к некоторому общему утверждению, а "дедукция" - получение результатов для частных случаев из некоторых общих утверждений, законов. В этом смысле метод математической индукции является дедуктивным, с его помощью доказываются общие утверждения (равенства, неравенства и т.п.). Он не дает способа для выдвижения общей гипотезы или угадывания общего правила или формулы по наблюдениям за отдельными частными случаями. Но этот метод позволяет проверять выдвинутые гипотезы. Для неверной гипотезы проверка провалится на шаге индукции.

Отметим также, что приведенная формулировка принципа математической индукции допускает разные эквивалентные варианты. В ряде случаев мы будем использовать вариант, в котором шаг индукции состоит в предположении справедливости P(n) при всех n <= k и доказательстве из этого предположения справедливости утверждения P(k+1).

Такая формулировка будет использоваться, в частности, при доказательствах индукцией по построению объекта.

В дискретной математике и в информатике многие классы объектов определяются индуктивно. В таких определениях явно или неявно участвует некоторая функция, задающая "сложность" объекта, и индукция идет по значениям этой функции. На базисном шаге определяются объекты минимальной сложности (обычно они имеют сложность 0), а индукционный шаг определения заключается в том, что из объектов меньшей сложности с помощью некоторых операций (операторов, конструкций) строятся объекты большей сложности.

Для доказательства некоторого свойства объектов индуктивно определенного класса метод математической индукции применяется в следующем виде.

Базис индукции состоит в проверке требуемого свойства у объектов минимальной сложности.
Шаг индукции состоит в предположении справедливости доказываемого свойства
у всех объектов класса, имеющих сложность <= k, и проверке того, что все объекты большей сложности (обычно, сложности k+1 ), получаемые из них с помощью используемых при определении класса операций, также обладают требуемым свойством.

Рассмотрим эту схему на примере простых арифметических выражений.

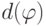Пример 2.1. Пусть V ={x, y, z} - множество переменных, O={+, -, *, / } - список операций. Определим индуктивно множество $\mathcal{A}$ выражений ( слов) в объединенном алфавите $\Sigma = V \cup O \cup \{ ( , )\}$ , называемых арифметическими формулами. Одновременно будем определять меру сложности этих формул, назывемую их глубиной. Глубину формулы $\phi$ обозначим через $d(\varphi )$ .

Базис индукции. Каждая переменная 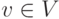$v \in V$ является арифметической формулой глубины 0, т.е. $v \in codecal\{ A\}$ и d(v)=0.
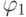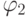Шаг индукции. Пусть и - арифметические формулы глубины 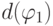и 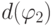, соответственно. Тогда выражения
- (а) $(\varphi _{1} + \varphi _{2})$ ,
- (б) $(\varphi _{1} - \varphi _{2})$ ,
- (в) $(\varphi _{1} * \varphi _{2})$ ,
- (г) $(\varphi _{1} / \varphi _{2})$ ,
также являются арифметическими формулами из $\mathcal{A}$ и каждая из этих формул имеет глубину $max\{ d(\varphi _{1}),d(\varphi _{2}) \} +1$ .

Пусть w=w₁w₂ ... w_n - произвольное слово в алфавите 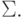$\Sigma.$ Скажем, что скобки в w расставлены правильно, если для каждого i <= n число левых скобок в слове w⁽ⁱ⁾=w₁w₂ ... w_i не меньше числа правых скобок, а во всем слове w число левых скобок равно числу правых.

Докажем, что в каждой арифметической формуле из $\mathcal{A}$ скобки расставлены правильно.

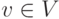Базис индукции. $d(\varphi )= 0$ . Формула глубины 0 является переменной $v \in V$ . В ней нет скобок и поэтому они расставлены правильно.
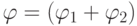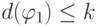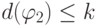Шаг индукции. Пусть утверждение справедливо для всех формул из $\mathcal{A}$ глубины <= k и $\phi$ - произвольная формула глубины $d(\varphi )= k+1$ . Тогда она имеет одну из четырех форм (а), (б), (в) или (г). Предположим, что $\varphi = (\varphi _{1} + \varphi _{2})$ . 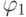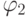Тогда из определения глубины следует, что $d(\varphi _{1})\le k$ и $d(\varphi _{2}) \le k$ , и по индукционному предположению в обеих формулах $\varphi _{1}$ и $\varphi _{2}$ скобки расставлены правильно. Покажем, что и в $\phi$ скобки расставлены правильно. Пусть $\varphi _{1}=\{v_{1}v_{2} \dots v_{m1}\}$ и $\varphi _{2}=\{w_{1}w_{2} \dots w_{m2}\}$ . 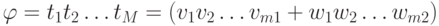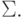Тогда $\varphi =t_{1}t_{2} \dots t_{M}= (v_{1}v_{2} \dots v_{m1}+w_{1}w_{2} \dots w_{m2})$ , здесь M= m₁+m₂ +3 и все символы v_i, w_j принадлежат алфавиту $\Sigma.$ Для каждого 1 < i <= m₁+1 число левых скобок в t₁ ... t_i на 1 больше числа левых скобок в v₁... v_i-1, и следовательно, больше числа правых скобок в этом слове, так все они входят в v₁... v_i-1. Это же справедливо для слова t₁t₂ ... t_m1+2, заканчивающегося символом +. При m₁+2 < i < M разница между числом левых и правых скобок в t₁ ... 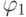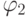t_i не меньше 1, так как t₁= (, а в $\varphi _{1}$ и $\varphi _{2}$ скобки расставлены правильно. 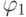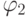Во всем слове $\phi$ число левых и правых скобок совпадает, так как к скобкам $\varphi _{1}$ и $\varphi _{2}$ добавилась одна левая и одна правая скобка. Таким образом, в $\phi$ скобки расставлены правильно. Случаи (б), (в) и (г) рассматриваются аналогично.

Задачи

Задача 2.1. Доказать, что

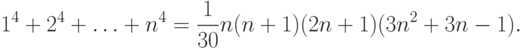
$1^4 +2^4 + \ldots + n^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1).$

Задача 2.2. Доказать, что

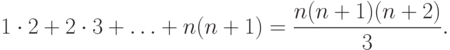
$1\cdot 2 +2\cdot 3 + \ldots + n(n+1) = \frac{n(n+1)(n+2)}{3}.$

Задача 2.3. Доказать, что

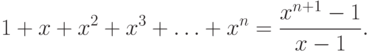
$1 + x+ x^2 +x^3 + \ldots + x^n =\frac{x^{n+1}-1}{x - 1}.$

Задача 2.4. Доказать, что n различных прямых на плоскости разбивают ее на области, которые можно закрасить белой и черной красками так, что смежные области будут закрашены разными красками.

Задача 2.5. Найдите ошибку в следующем доказательстве "по индукции" утверждения:

для всех n >= 1 справедливо неравенство 3ⁿ > 3(n +1) +1 .

Доказательство Пусть для некоторого k >= 1 неравенство справедливо, т.е. 3^k > 3(k +1) +1 (*). Докажем, что оно верно и для n=k+1, т.е. 3^k+1 > 3(k+2) +1. Для этого заметим, что для любого k >= 1 верно неравенство 2 cdot 3^k > 3. Прибавив его левую и правую часть к соответствующим частям неравенства (*), получим 3^k + 2 x 3^k > 3(k +1) +1+3 или 3^k+1 > 3(k+2) +1, что и требовалось. Установите, при каких n справедливо неравенство 3ⁿ > 3(n +1)+1.

Дальше >>

Авторизоваться

Основы дискретной математики

Индукция и комбинаторика

Метод математической индукции

Задачи

Вопросы и ответы