|
Это в лекции 3. |
Булевы функции и их представления
Булевы функции от 1-ой и 2-х переменных
Представим вначале в табличном виде все булевы функции от 1-ой переменной. Как мы знаем, их всего четыре.
В этой таблице представлены следующие функции:
- f1(x1)= 0 - константа 0;
- f2(x1)= 1 - константа 1;
- f3(x1)= x1 - тождественная функция;
-
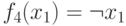 - отрицание x1
(используется также обозначение x
1
,
а в языках программирования эта функция часто обозначается как NOTx1
).
- отрицание x1
(используется также обозначение x
1
,
а в языках программирования эта функция часто обозначается как NOTx1
).
В следующей таблице представлены все 16 функций от 2-х переменных.
Многие из этих функций часто используются в качестве "элементарных" и имеют собственные обозначения.
- f1(x1,x2)= 0 - константа 0;
- f2(x1,x2)= 1 - константа 1;
- f3(x1,x2)= x1 - функция, равная 1-му аргументу ;
-
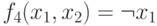 - отрицание x1
;
- отрицание x1
; - f5(x1,x2)= x2 - функция, равная 2-му аргументу ;
-
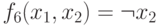 - отрицание x2
;
- отрицание x2
; -
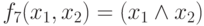 - конъюнкция,
читается " x1
и x2
"
(используются также обозначения (x1 & x2)
, (x1x2)
, min(x1,x2)
и (x1 AND x2)
);
- конъюнкция,
читается " x1
и x2
"
(используются также обозначения (x1 & x2)
, (x1x2)
, min(x1,x2)
и (x1 AND x2)
); -
 - дизъюнкция,
читается " x1
или x2
"
(используются также обозначения
- дизъюнкция,
читается " x1
или x2
"
(используются также обозначения 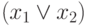 , (x1 + x2)
, max(x1,x2)
и (x1 OR x2)
);
, (x1 + x2)
, max(x1,x2)
и (x1 OR x2)
); -
f9(x1,x2)= (x1 -> x2)
- импликация,
читается " x_1 влечет x_2 "
или "из x1
следует x2
"
(используются также обозначения (
 ), и ( IF x1 THEN x2
));
), и ( IF x1 THEN x2
)); -
f10(x1,x2)= (x1 + x2)
- сложение по модулю 2,
читается " x1
плюс x2
"
(используется также обозначение
 );
); -
f11(x1,x2)= (x1 ~ x2)
- эквивалентность,
читается " x1
эквивалентно (равносильно) x2
"
(используется также обозначение
 );
); - f12(x1,x2)= (x1 | x2) - штрих Шеффера (антиконъюнкция), иногда читается как "не x1 и x2 ";
-
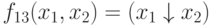 - стрелка
Пирса (антидизъюнкция), иногда читается как "не x1
или x2
".
- стрелка
Пирса (антидизъюнкция), иногда читается как "не x1
или x2
".
В качестве элементарных функций будем также рассматривать 0-местные функции-константы 0 и 1.
Отметим, что функции f1(x1,x2) и f2(x1,x2) фактически не зависят от значений обоих аргументов, функции f3(x1,x2) и f4(x1,x2) не зависят от значений аргумента x2, а функции f5(x1,x2) и f6(x1,x2) не зависят от значений аргумента x1.
Определение 3.1.
Функция f(x1,..., xi,..., xn) не зависит от аргумента xi, если для любого набора значений  остальных аргументов f имеет место равенство
остальных аргументов f имеет место равенство
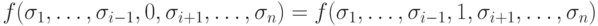
Такой аргумент xi называется фиктивным. Аргументы, не являющиеся фиктивными, называются существенными.
Функции f1(x1,..., xn) и f2(x1,...,xm) называются равными, если функцию f2 можно получить из функции f1 путем добавления и удаления фиктивных аргументов.
Например, равными являются одноместная функция f3(x1) и двухместная функция f3(x1,x2) , так как вторая получается из первой добавлением фиктивного аргумента x2 . Мы не будем различать равные функции и, как правило, будем использовать для обозначения равных функций одно и то же имя функции. В частности, это позволяет считать, что во всяком конечном множестве функций все функции зависят от одного и того же множества переменных.
Формулы
Как мы видели, геометрическое и табличное представления булевых функций подходят лишь для функций с небольшим числом аргументов. Формулы позволяют удобно представлять многие функции от большего числа аргументов и оперировать различными представлениями одной и той же функции.
Пусть 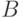 - некоторое (конечное или бесконечное)
множество булевых функций. Зафиксируем некоторое счетное множество
переменных V={X1, X2, ...}
.
Определим по индукции множество формул над
- некоторое (конечное или бесконечное)
множество булевых функций. Зафиксируем некоторое счетное множество
переменных V={X1, X2, ...}
.
Определим по индукции множество формул над 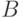 с
переменными из V. Одновременно будем определять числовую характеристику
с
переменными из V. Одновременно будем определять числовую характеристику  формулы
формулы  называемую ее глубиной,
и множество ее подформул.
называемую ее глубиной,
и множество ее подформул.
Определение 3.2.
-
Базис индукции. Каждая переменная
 и каждая
константа
и каждая
константа 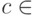
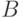 является формулой глубины 0, т.е. dep(Xi)= dep(c)=0
. Множество ее подформул
состоит из нее самой.
является формулой глубины 0, т.е. dep(Xi)= dep(c)=0
. Множество ее подформул
состоит из нее самой. -
Шаг индукции. Пусть
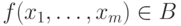 и A1, ... , Am
- формулы, и max {dep(Ai) | i = 1,..., m} = k
.
Тогда выражение
и A1, ... , Am
- формулы, и max {dep(Ai) | i = 1,..., m} = k
.
Тогда выражение 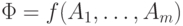 является формулой, ее глубина
является формулой, ее глубина  равна k+1, а
множество подформул
равна k+1, а
множество подформул  включает
саму формулу
включает
саму формулу  и все подформулы формул A1, ..., Am.
и все подформулы формул A1, ..., Am.
Каждой формуле 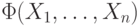 сопоставим булеву
функцию, которую эта формула задает, используя индукцию по глубине
формулы.
сопоставим булеву
функцию, которую эта формула задает, используя индукцию по глубине
формулы.
Базис индукции. Пусть 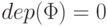 . Тогда
. Тогда 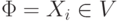 или
или 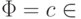
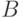 .
В первом случае
.
В первом случае  задает функцию
задает функцию 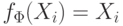 , во втором - функцию, тождественно равную
константе c.
, во втором - функцию, тождественно равную
константе c.
Шаг индукции. Пусть  - произвольная формула глубины
- произвольная формула глубины 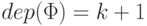 .
Тогда
.
Тогда 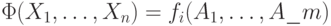 , где
, где 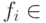
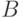 и A1, ..., Am
- формулы,
для которых max1 <= i <= m{dep(Ai)}=k
. Предположим (по
индукции), что этим формулам уже сопоставлены функции g1(X1,..., Xn), ... , gm(X1,..., Xn)
. Тогда
формула
и A1, ..., Am
- формулы,
для которых max1 <= i <= m{dep(Ai)}=k
. Предположим (по
индукции), что этим формулам уже сопоставлены функции g1(X1,..., Xn), ... , gm(X1,..., Xn)
. Тогда
формула  задает функцию
задает функцию 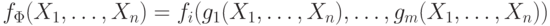 .
.
Далее мы будем рассматривать формулы над множеством элементарных функций 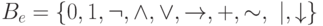 . Все эти функции, кроме констант, называются логическими связками или логическими операциями.
При этом для 2-местных функций из этого списка будем использовать инфиксную запись,
в которой имя логической связки помещается между 1-ым и 2-ым аргументами.
Тогда определение формулы над
. Все эти функции, кроме констант, называются логическими связками или логическими операциями.
При этом для 2-местных функций из этого списка будем использовать инфиксную запись,
в которой имя логической связки помещается между 1-ым и 2-ым аргументами.
Тогда определение формулы над 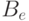 имеет следующий вид.
имеет следующий вид.
Определение 3.3.
-
Базис индукции. 0, 1 и каждая переменная
 являются формулами глубины 0.
являются формулами глубины 0. -
Шаг индукции. Пусть
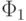 и
и  - формулы,
- формулы, 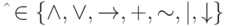 .
.
Тогда выражения  и
и 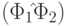 являются формулами. При этом
являются формулами. При этом  ,
а
,
а  .
.
В соответствии с этим определением выражения 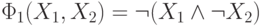 и
и 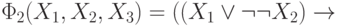
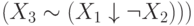 являются формулами. Глубина
являются формулами. Глубина 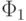 равна 3, а глубина
равна 3, а глубина  равна 4.
Выражения же
равна 4.
Выражения же 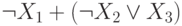 ,
,  и (X1 + X2 + X3)
формулами не являются (почему?).
и (X1 + X2 + X3)
формулами не являются (почему?).
Для определения функции, задаваемой формулой, удобно использовать таблицу,
строки которой сответствуют наборам значений переменных, а в столбце под знаком
каждой логической связки стоят значения функции, задаваемой соответствующей подформулой.
Например, для формулы  функция
функция  задается выделенным столбцом
задается выделенным столбцом  следующей таблицы.
следующей таблицы.