Дифференцирование
Теорема(признак монотонности функции). Для того чтобы функция f(x) была монотонной на промежутке X, необходимо и достаточно, чтобы f'(x) не меняла свой знак на всем промежутке. При этом, если f'(x)>0, то функция возрастает на этом промежутке, а если f'(x)<0 - то убывает. Если при этом допускается и равенство нулю производной в каких-то точках, то говорят о нестрогом возрастании или убывании.
Приведите геометрическое обоснование этого утверждения и иллюстрирующий рисунок.
Правило исследования монотонности дифференцируемой функции:
- Найти все критические точки xi (i=1,2,...,n), то есть точки, где производная равна нулю, или не существует, или бесконечна.
- Исследовать знак производной f'(x) на каждом промежутке между этими точками, то есть на промежутках (xi;xi+1), i=1,2,...,n-1. Если f'(x)>0 на (xi;xi+1), то функция f(x) строго возрастает на этом интервале; если f'(x)<0, то f(x) - строго убывает; если
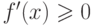 , то f(x) - нестрого возрастает (не убывает); если
, то f(x) - нестрого возрастает (не убывает); если 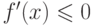 , то f(x) - нестрого убывает (не возрастает).
, то f(x) - нестрого убывает (не возрастает).
Функция (геометрически - график функции) f(x) называется выпуклой (вогнутой) в точке x0, если существует  -окрестность, в которой все точки графика функции расположены ниже (выше - для вогнутой) касательной к кривой f(x) в точке x0. Точки, в которых выпуклости функции меняются на вогнутости, называются точками перегиба.
-окрестность, в которой все точки графика функции расположены ниже (выше - для вогнутой) касательной к кривой f(x) в точке x0. Точки, в которых выпуклости функции меняются на вогнутости, называются точками перегиба.
Теорема(признак выпуклости или вогнутости функции).
Если в каждой точке 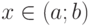 вторая производная функции f''(x)>0, то кривая y=f(x) вогнута на этом промежутке. Если в каждой точке
вторая производная функции f''(x)>0, то кривая y=f(x) вогнута на этом промежутке. Если в каждой точке 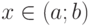 производная f''(x)<0, то кривая y=f(x) выпукла на промежутке.
производная f''(x)<0, то кривая y=f(x) выпукла на промежутке.
Асимптотой для графика функции y=f(x) называется прямая, которую график y=f(x) никогда не может пересечь, приближаясь неограниченно к ней.
Есть три вида асимптот: вертикальные асимптоты, уравнения которых имеют вид x=a, горизонтальные асимптоты с уравнениями y=b и наклонные асимптоты с общим уравнением прямой вида y=kx+b.
Для наклонной асимптоты параметры прямой определяются из соотношений вида
![k=\lim\limits_{x\to \infty} \frac {f(x)}{x}, \\
b=\lim\limits_{x\to \infty} [f(x)-kx].](/sites/default/files/tex_cache/3523d23a5e9b307a0cfc881a0c7f46d2.png)
Для исследования указанных выше свойств функции f(x) используют обычно следующую (упрощенную) схему:
- Найти область определения D(f), область изменения функции E(f).
- Исследовать функцию на четность или нечетность (каковы оси симметрии графика функции), на периодичность (какие участки графика повторяются).
- Найти точки разрыва (если они есть), то есть разбить область D(f) на области
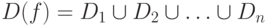 , в каждой из которых функция f(x) - непрерывна.
, в каждой из которых функция f(x) - непрерывна. - Найти асимптоты (вертикальные, горизонтальные или наклонные).
- Найти точки экстремума и экстремумы функции.
- Найти интервалы монотонности (возрастания и убывания) функции.
- Найти интервалы выпуклости, вогнутости кривой, точки ее перегиба.
- Найти точки пересечения кривой с осями координат, если они существуют, то есть решение уравнения f(x0)=0 (A(x0;0) - точка пересечения с осью Ox ) и f(0)=y0 (B(0; y0) - точка пересечения с осью Oy ).
- Построить график функции, используя результаты п. 1-8.
Рассмотрим теперь функцию двух переменных z=f(x,y).
Если существует конечный предел отношения приращения функции по переменной x (обозначим приращение 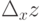 ) к приращению аргумента, то есть
) к приращению аргумента, то есть
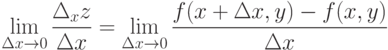
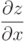 ,
,  , zx, fx. Таким образом,
, zx, fx. Таким образом,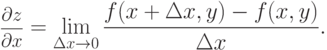
Аналогично вводится частная производная по y:

Вычисление частных производных по x и по y производится по известным для функции одной переменной правилам, причем при нахождении 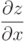 этой переменной считается переменная x (переменная y выполняет роль числового параметра при этом), а при нахождении
этой переменной считается переменная x (переменная y выполняет роль числового параметра при этом), а при нахождении 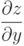 этой переменной является y (переменная x при этом будет параметром).
этой переменной является y (переменная x при этом будет параметром).
Пример. Вычислим частные производные некоторых функций
- Функция z=x2a+a2 является функцией одной переменной x, a - параметр, поэтому ищем не частную, а обычную производную (от одной переменной): z'(x)=2ax+0=2ax.
- Функция z=x2y+y2 является функцией двух переменных x и y. Находим частные производные:
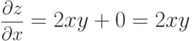 ,
, 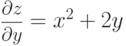 .
. - Функция двух переменных
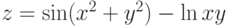 . Найдем частные производные:
. Найдем частные производные:
Производные второго и далее порядка определяются как производные от производных предыдущего порядка.
Пример.
Для функции 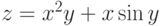 можно рассматривать две производные первого порядка
можно рассматривать две производные первого порядка 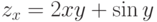 ,
, 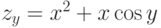 и четыре производные второго порядка: zxx=(zx)x=2y+0=2y,
и четыре производные второго порядка: zxx=(zx)x=2y+0=2y, 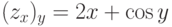 ,
, 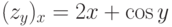 ,
,  . Как отсюда видно, производные (zx)y и (zy)x равны. Справедливо более общее следующее утверждение.
. Как отсюда видно, производные (zx)y и (zy)x равны. Справедливо более общее следующее утверждение.
Теорема(о равенстве смешанных производных). Смешанные производные zxy и zyx для любой функции z=f(x,y), у которой обе эти производные существуют, равны между собой в любой допустимой точке.
Такая теорема справедлива и относительно смешанных производных функций трех, четырех и т.д. переменных.
Пример. Для функции трех переменных u=f(x,y,z) равны, в частности, смешанные производные: uxyy=uyyx, uxyz=uyzx.
Пусть z=f(x,y) определена в области D(f).
Точка (x0;y0) называется точкой максимума ( минимума ) функции z=f(x,y), если существует  -окрестность точки (x0;y0) такая, что
-окрестность точки (x0;y0) такая, что 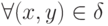 -окрестности: f(x,y) < f(x0,y0) ( f(x,y) > f(x0,y0)). Эти точки называются точками экстремума .
-окрестности: f(x,y) < f(x0,y0) ( f(x,y) > f(x0,y0)). Эти точки называются точками экстремума .
Теорема(необходимое условие экстремума).
Если функция двух переменных имеет экстремум в точке  , то либо все ее частные производные первого порядка равны нулю, то есть
, то либо все ее частные производные первого порядка равны нулю, то есть 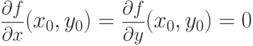 , либо хотя бы одна из них не существует.
, либо хотя бы одна из них не существует.
Точки функции f(x,y), в которых fx=0, fy=0 или же эти производные не существуют, называются критическими точками .
Если функция f(x,y) имеет экстремум, то его необходимо искать среди значений функции в критических точках.
Для нахождения критических точек нужно решить систему уравнений
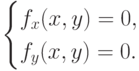
Теорема(достаточное условие экстремума).
Пусть (x0;y0) - критическая точка функции f(x,y), которая имеет вторые производные, непрерывные в  -окрестности некоторой критической точки (x0,y0). Если
-окрестности некоторой критической точки (x0,y0). Если 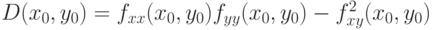 , то
, то
- прив точке (x0,y0) имеем максимум;
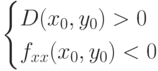
- прив точке имеем минимум;
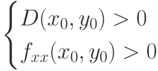
- при D(x0,y0) <0 - в точке (x0,y0) нет экстремума;
- при D(x0,y0)=0 - в точке (x0,y0) экстремум может быть или не быть.
Если мы работаем с функцией z=f(x1,x2,...,xn), то необходимое условие экстремума будет  .
.
Иногда приходится иметь дело с экстремумом функции, который ищут среди точек x, y, удовлетворяющих одному или нескольким условиям связи вида 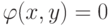 . Такие экстремумы называются условными экстремумами или экстремумами с ограничениями.
. Такие экстремумы называются условными экстремумами или экстремумами с ограничениями.
