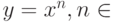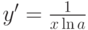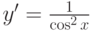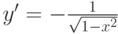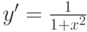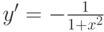НОУ ИНТУИТ | Введение в математику. Лекция 8: Дифференцирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Кабардино-Балкарский государственный университет

Опубликован: 18.04.2007 | Доступ: свободный | Студентов: 12046 / 2526 | Оценка: 4.16 / 4.04 | Длительность: 14:52:00

ISBN: 978-5-9556-0105-2

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Пример. Рассмотрим некоторые применения указанных теорем (формул):

1. $(\ln (x^2+\sin x))'=\frac {1}{x^2+\sin x}\cdot (x^2+\sin x)' = \frac {2x+\cos x}{x^2+\sin x}$ .

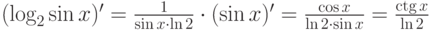2. $(\log_2 \sin x)' = \frac {1}{\sin x\cdot \ln 2}\cdot (\sin x)' = \frac {\cos x}{\ln 2\cdot \sin x}=\frac {\ctg x}{\ln 2}$ .

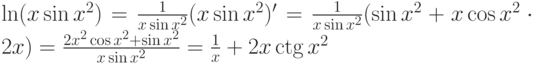3. $\ln (x\sin x^2) = \frac {1}{x\sin x^2} (x\sin x^2)' = \frac {1}{x\sin x^2} (\sin x^2+x\cos x^2\cdot 2x) = \frac {2x^2\cos x^2+\sin x^2}{x\sin x^2} = \frac 1x +2x \ctg x^2$ .

4. y=x²e^x $\implies$ y'=2xe^x +x² e^x.

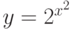
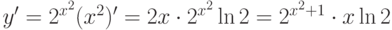5. $y=2^{x^2}$ $\implies$ $y'=2^{x^2} (x^2)' = 2x\cdot 2^{x^2}\ln 2 = 2^{x^2+1} \cdot x\ln 2$ .

6. e^{sin x+cos x} = e^{sin x+cos x}(sin x+cos x)' = e^{sin x+cos x} (cos x-sin x).

Теорема. Если функция y=f(x) имеет обратную функцию 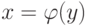$x=\varphi (y)$ (то есть функцию с 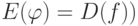$D(\varphi )=E(f)$ , $E(\varphi )=D(f))$ , которая в точке 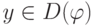$y\in D(\varphi )$ имеет производную 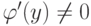$\varphi '(y)\ne 0$ , то в точке 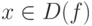$x\in D(f)$ функция y=f(x) имеет производную

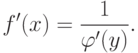
$f'(x) = \frac {1}{\varphi '(y)}.$

Следствие.

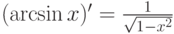$(\arcsin x)'=\frac {1}{\sqrt{1-x^2}}$ .
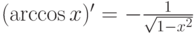$(\arccos x)' = -\frac {1}{\sqrt{1-x^2}}$ .
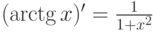$(\arctg x)' = \frac {1}{1+x^2}$ .
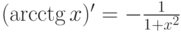$(\arcctg x)'= -\frac {1}{1+x^2}$ .

Пример. Рассмотрим примеры использования этих формул:

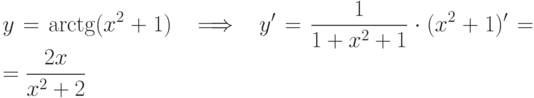$\displaystyle y=\arctg (x^2+1) \ \implies \ y'=\frac {1}{1+x^2+1}\cdot (x^2+1)' = \frac {2x}{x^2+2}$ .
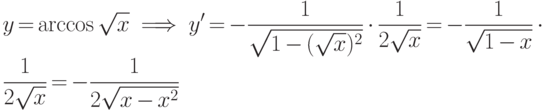$\smu{2.7}\displaystyle y=\arccos \sqrt{x}\ \implies \ y'=-\frac {1}{\sqrt{1-(\sqrt{x})^2}}\cdot \frac {1}{2\sqrt{x}} = -\frac {1}{\sqrt{1-x}}\cdot \frac {1}{2\sqrt{x}} ={-}\frac {1}{2\sqrt{x-x^2}}$ .

Следует понять и запомнить основную таблицу дифференциального исчисления.

Таблица основных формул дифференцирования
№	Функция	Производная
1	y=c	y'=0
2	$y=x^n, n\in\R$	y'=nx^n-1
3	y=a^x	y'=a^x ln a
4	y=log_a x	$y'=\frac {1}{x\ln a}$
5	y=sin x	y'=cos x
6	y=cos x	y'=-sin x
7	y=tg x	$y'=\frac {1}{\cos ^2x}$
8	y=ctg x	$y'=-\frac {1}{\sin^2x}$
9	y=sec x	$y'=\sec x\cdot \tg x$
10	y=cosec x	$y'=-\cosec x\cdot \ctg x$
11	y=arcsin x	$y'=\frac {1}{\sqrt{1-x^2}}$
12	y=arccos x	$y'=-\frac {1}{\sqrt{1-x^2}}$
13	y=arctg x	$y'=\frac {1}{1+x^2}$
14	y=arcctg x	$y'=-\frac {1}{1+x^2}$

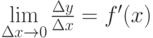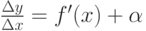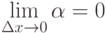Пусть функция y=f(x) имеет в точке x производную $\lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x} =f'(x)$ . Тогда, используя определение предела и бесконечно малой величины, имеем $\frac {\Delta y}{\Delta x}=f'(x)+\alpha$ , где $\lim\limits_{\Delta x\to 0}\alpha =0$ . Отсюда получаем

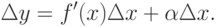
$\Delta y =f'(x)\Delta x+\alpha \Delta x.$

Дифференциалом функции f(x) в точке x называется главная, линейная относительно 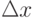$\Delta x$ , часть приращения функции. Обозначают дифференциал dy или df(x):

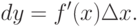
$dy = f'(x)\Delta x.$

Если y=f(x) дифференцируема $\forall x\in X$ , то f'(x) - функция от x. Допустим, что опять дифференцируема, тогда (f'(x))' называется второй производной функции y=f(x) . Обозначается вторая производная y'' (читается игрек два штриха). Производная от второй производной, если она существует, называется третьей производной и т.д.

Пример. Пусть y=cos x, y'=-sin x, y''=-cos x, y'''=sin x, 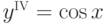$y^{\scriptscriptstyle\fam0 IV}=\cos x$ - циклически повторяемая последовательность производных функции y=cos x.

Производная функции помогает определять качественные и количественные характеристики, свойства любых функций - находить максимумы и минимумы, наибольшее и наименьшее значения, выяснять промежутки возрастания и убывания функции, выпуклости и вогнутости и т.д. Рассмотрим некоторые из них.

Функция y=f(x) имеет минимум ( максимум ) в точке x₀, если существует такая окрестность точки x₀: 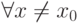$\forall x\ne x_0$ и в этой окрестности имеет место неравенство f(x₀)<f(x) (f(x₀)> f(x)). Точка x₀, в которой функция имеет минимум или максимум называется точкой экстремума , а само значение f(x₀) - экстремумом функции.

Точки, в которых функция может достигать экстремума, определяются следующей теоремой.

Теорема Ферма (необходимое условие существования экстремума). Для того, чтобы дифференцируемая в точке x₀ функция y=f(x) имела в этой точке экстремум, необходимо, чтобы f'(x₀)=0.

Точка x₀, в которой производная равна нулю или не существует, называется критической точкой .

Теорема Ферма отвечает полностью на вопрос, в каких точках функция не имеет экстремум (в точках, где 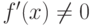$f'(x)\ne 0$ ), но не определяет, имеется ли в данной точке x₀ экстремум или нет. На этот вопрос отвечает следующая теорема.

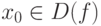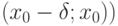Теорема(достаточный признак экстремума по первой производной). Если $x_0\in D(f)$ - критическая точка функции f(x) и существует такая $\delta$ -окрестность, что слева (то есть в интервале $(x_0-\delta ; x_0))$ и справа от точки x₀ (то есть в интервале 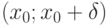$(x_0;x_0+\delta)$ ) производная f'(x) имеет разные знаки, то в точке x₀ функция имеет экстремум (максимум или минимум), причем:

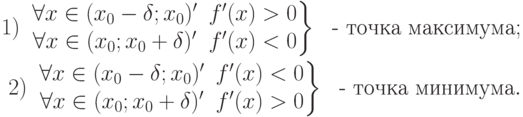
$\begin{align*} 1) \ \left. \begin{matrix} \forall x\in (x_0-\delta ; x_0) '\ & f'(x)>0 \cr \forall x\in (x_0; x_0+\delta ) '\ & f'(x)<0 \end{matrix} \right \}\ \text{ - точка максимума}; \\ 2) \ \left. \begin{matrix} \forall x\in (x_0-\delta ; x_0) '\ & f'(x)<0 \cr \forall x\in (x_0; x_0+\delta ) '\ & f'(x)>0 \end{matrix} \right \}\ \text{ - точка минимума}. \end{align*}$

Из этих теорем следует правило 1 нахождения экстремума функции:

Найти все критические точки f(x) на D(f), то есть точки x_i, i=1,2,...,n 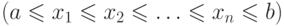$(a\le x_1\le x_2\le \dotsc\le x_n\le b)$ , в которых выполнено хотя бы одно из условий: f'(x)=0, $f'(x)=\pm \infty$ , f'(x) не существует.
Установить знаки производной f'(x) в каждом интервале (a;x₁), (x₁;x₂), (x₂;x₃ ), ..., (x_n;b).
Если знак при переходе через точку x_i (i=1,2,...,n) меняет свой знак с плюса на минус, то в точке x_i функция f(x) имеет максимум, а если меняет знак с минуса на плюс, то - минимум. Для определения знака в (x_i;x_i+1) можно взять любую контрольную точку из этого промежутка.

Теорема(достаточный признак экстремума по второй производной). Если функция f(x) имеет вторую производную в окрестности точки x₀ и f'(x₀)=0, 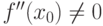$f''(x_0)\ne 0$ , то в точке x₀ функция имеет экстремум, причем, если f''(x₀)<0, то имеется максимум, а если f''(x₀)>0, то - минимум.

Из этой теоремы следует правило 2 нахождения экстремума функции:

Найти критические точки x_i (i=1,2,...,n).
Найти знаки .
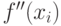Если 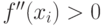, то в точке x_i - минимум, если 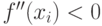, то - максимум.

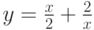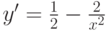
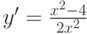Пример. Пусть $y=\frac x2+\frac 2x$ на [-5; 5], $y'=\frac 12-\frac {2}{x^2}$ $\implies$ $y'=\frac {x^2-4}{2x^2}$ y'=0 $\implies$ $x_{1{,}2}=\pm 2$ . Критические точки x₁=-2, x₂=2, x₃=0 (в последней точке производная не существует). Исследуем экстремумы функции. 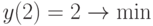По правилу 1 исследуем y' на интервалах: (-5; -2), (-2; 0), (0;2), (2; 5), y'(-3)>0, y'(3)>0, y'(-1)<0 и, следовательно, x=-2 - точка максимума, x=2 - точка минимума, x=0 - нет экстремума, экстремумы равны y(-2)=-2 (максимум), y(2)=2 (минимум) $y(-2) =-2\to \max$ $y(2)=2\to \min$ . 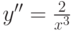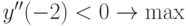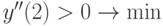По правилу 2 можно заключить следующее: $y''= \frac {2}{x^3}$ , $y''(-2) <0\to \max$ , $y''(2) >0\to \min$ .

По теореме Вейерштрасса, функция f(x), непрерывная на [a;b], принимает на этом промежутке наибольшее и наименьшее значение. Это значение может достигаться либо в критической точке, либо на концах [a;b], то есть можно будет записать:

$\begin{align*} & y' _{\substack {\max} {[a,b]}} =\max \{\text{значения функции в критических точках}, \ y(a), \ y(b)\}, \\ & y' _{\gen\frac {}{}{0pt}{-1} {\min} {[a,b]}} =\max \{\text{значения функции в критических точках}, \ y(a), \ y(b)\}. \end{align*}$

Теорема(признак постоянства функции). Если $\forall x\in X$ имеем f'(x)=0, то f(x)=const на всем множестве X.

Простейшим геометрическим подтверждением этой теоремы является тот факт, что если производная функции в каждой точке равна нулю, то угловой коэффициент касательной к ней в любой точке равен нулю, то есть касательная к графику в любой точке горизонтальна ( 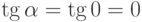$\tg\alpha =\tg0=0$ ), следовательно, график самой функции - горизонтальная прямая. Постройте соответствующий рисунок.

Дальше >>

Авторизоваться

Введение в математику

Дифференцирование

Вопросы и ответы