Методы сжатия без потерь

Теперь запишем алгоритм сжатия, используя целочисленные операции. Минимизация потерь по точности достигается благодаря тому, что длина целочисленного интервала всегда не менее половины всего интервала. Когда 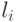или одновременно находятся в верхней или нижней половине ( Half ) интервала, то мы просто записываем их одинаковые верхние биты в выходной поток, вдвое увеличивая интервал. Если 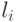и приближаются к середине интервала, оставаясь по разные стороны от его середины, то мы также вдвое увеличиваем интервал, записывая биты "условно". "Условно" означает, что реально эти биты выводятся в выходной файл позднее, когда становится известно их значение. Процедура изменения значени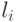й и называется нормализацией, а вывод соответствующих битов - переносом. Знаменатель дроби в приведенном ниже алгоритме будет равен , т.е. максимальное значение .

l0=0; h0=65535; i=0; delitel= b[clast]; // delitel=10
First_qtr = (h0+1)/4;    // = 16384
Half = First_qtr*2;     // = 32768
Third_qtr = First_qtr*3;// = 49152
bits_to_follow =0;      // Сколько битов сбрасывать

while(not DataFile.EOF()) {
	c = DataFile.ReadSymbol();  // Читаем символ
	j = IndexForSymbol(c); i++; // Находим его индекс 
	li = li-1 + b[j-1]*(hi-1 - li-1 + 1)/delitel;
	hi = hi-1 + b[j]*(hi-1 - li-1 + 1)/delitel - 1;
	for(;;) {         	// Обрабатываем варианты 
		if(hi < Half)   	// переполнения
			BitsPlusFollow(0);
		else if(li >= Half) {
			BitsPlusFollow(1);
			li-= Half; hi-= Half;
		}
		else if((li >= Third_qtr)&&(hi < First_qtr)){
			bits_to_follow++;
			li-= First_qtr; hi-= First_qtr;
		} else break;
		li+=li; hi+= hi+1;
	}
}    
           // Процедура переноса найденных битов в файл
void BitsPlusFollow(int bit)
{
	CompressedFile.WriteBit(bit);
	for(; bits_to_follow > 0; bits_to_follow--)
		CompressedFile.WriteBit(!bit);
}

Результаты работы алгоритма представлены в табл. 1.3

Таблица 1.3.

	Символ ( 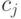)			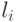Нормализованный	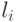Нормализованный	Результат
0		0	65535
1	К	19660	32767	13104	65535	01
2	О	13104	28832	26208	57665	010
3	В	41937	48227	7816	58143	010101
4	.	53111	58143	15836	35967	01010111
5	К	21875	25901	21964	38071	0101011101
6	О	21964	26795	22320	41647	010101110101

На символ с меньшей вероятностью у нас тратится в целом большее число битов, чем на символ с большей вероятностью. Алгоритм декомпрессии в целочисленной арифметике можно записать так:

l0=0; h0=65535; delitel= b[clast];
First_qtr = (h0+1)/4;    	// = 16384
Half = First_qtr*2;     	// = 32768
Third_qtr = First_qtr*3;	// = 49152

value=CompressedFile.Read16Bit();
for(i=1; i< CompressedFile.DataLength(); i++){
	freq=((value-li-1+1)*delitel-1)/(hi-1 - li-1 + 1);
	for(j=1; b[j]<=freq; j++);   // Поиск символа
	
	li = li-1 + b[j-1]*(hi-1 - li-1 + 1)/delitel;
	hi = hi-1 + b[j  ]*(hi-1 - li-1 + 1)/delitel - 1;

	for(;;) {         	// Обрабатываем варианты 
		if(hi < Half)   	// переполнения
			; // Ничего
		else if(li >= Half) {
			li-= Half; hi-= Half; value-= Half;
		}
		else if((li >= Third_qtr)&&(hi < First_qtr)){
			li-= First_qtr; hi-= First_qtr;
			value-= First_qtr;
		} else break;
		li+=li; hi+= hi+1;
		value+=value+CompressedFile.ReadBit();
	}
	DataFile.WriteSymbol(c);
};

Как видно, с неточностями арифметики мы боремся, выполняя отдельные операции над 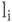и синхронно в компрессоре и декомпрессоре.

Незначительные потери точности (доли процента при достаточно большом файле) и, соответственно, уменьшение степени сжатия по сравнению с идеальным алгоритмом происходят во время операции деления, при округлении относительных частот до целого, при записи последних битов в файл. Алгоритм можно ускорить, если представлять относительные частоты так, чтобы делитель был степенью двойки (т.е. заменить деление операцией побитового сдвига).

Для того, чтобы оценить степень сжатия арифметическим алгоритмом конкретной строки, нужно найти минимальное число , такое, что длина рабочего интервала при сжатии последнего символа цепочки была бы меньше . Этот критерий означает, что внутри нашего интервала заведомо найдется хотя бы одно число, в двоичном представлении которого после -го знака будут только 0. Длину же интервала посчитать просто, поскольку она равна произведению вероятностей всех символов.

Рассмотрим приводившийся ранее пример строки из двух символов и с вероятностями 253/256 и 3/256. Длина последнего рабочего интервала для цепочки из 256 символов и с указанными вероятностями равна:

Легко подсчитать, что искомое ( ), поскольку 23 дает слишком большой интервал (в 2 раза шире), а 25 не является минимальным числом, удовлетворяющим критерию. Выше было показано, что алгоритм Хаффмана кодирует данную цепочку в 256 битов. Т.е. для рассмотренного примера арифметический алгоритм дает десятикратное преимущество, перед алгоритмом Хаффмана и требует менее 0.1 бита на символ.

Следует сказать пару слов об адаптивном алгоритме арифметического сжатия. Его идея заключается в том, чтобы перестраивать таблицу вероятностей по ходу упаковки и распаковки непосредственно при получении очередного символа. Такой алгоритм не требует сохранения значений вероятностей символов в выходной файл и, как правило, дает большую степень сжатия. Так, например, файл вида (где степень означает число повторов данного символа), адаптивный алгоритм сможет сжать эффективнее, чем потратив 2 бита на символ. Приведенный выше алгоритм достаточно просто превращается в адаптивный. Ранее мы сохраняли таблицу диапазонов в файл, а теперь мы считаем, прямо по ходу работы компрессора и декомпрессора, пересчитываем относительные частоты, корректируя в соответствии с ними таблицу диапазонов. Важно, чтобы изменения в таблице происходили в компрессоре и декомпрессоре синхронно, т.е. например, после кодирования цепочки длины 100 таблица диапазонов должна быть точно такой же, как и после декодирования цепочки длины 100. Это условие легко выполнить, если изменять таблицу после кодирования и декодирования очередного символа. Подробнее об адаптивных алгоритмах смотрите в главе "Методы контекстного моделирования".