Графика
Построение графика функции с условием
Функция может быть задана разными формулами на разных участках изменения аргумента. При задании функции можно использовать условную функцию.
Пример 3.2
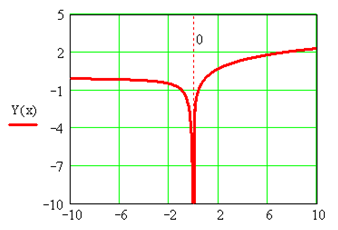
Построить график функции Y(x), заданной следующим образом:
Y=ln(x), x>0 Y=1/x, x<=0
Используем условную функцию if(cond, x, y)
Условная функция возвращает x , если условие cond есть true, возвращает y, если условие есть false. Условий может быть несколько.
На графике (Рис.3.8) нанесена риска x=0
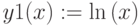 ,
, 
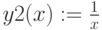 ,
, 
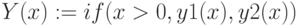
Условную функцию удобно использовать при построении области определения функции. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. С помощью условной функции можно показать график области допустимых значений .
Пример 3.3
Построить область определения функции 
Ведем функцию 
тогда 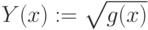
Область допустимых значений 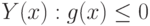
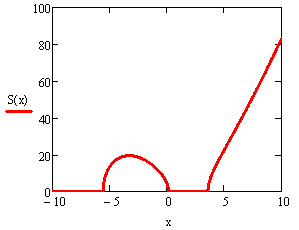
Строим функцию S(x), используя условную функцию
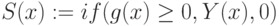
Строим график функции S(x) (Рис.3.9)
Построение графика функции для табулированных значений
Часто бывает необходимо построить график по точкам. Для этого аргумент и функция вводятся как индексные переменные от номера точки, номер точки – ранжированная переменная.
Пример 3.4
Построить график функции  по 15 точкам, x меняется от 0 до 1,5 с шагом = 0,1:
по 15 точкам, x меняется от 0 до 1,5 с шагом = 0,1:
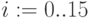 ,
, 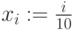 ,
, 
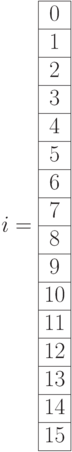
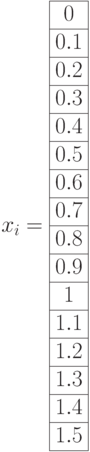

- Ввести номер точки i как ранжированную переменную.
- Ввести xi как с индексную переменную. Ввести функцию с индексом
 . Построить таблицы значений аргумента и функции в виде вектор-столбцов.:
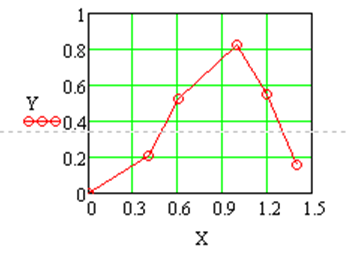
. Построить таблицы значений аргумента и функции в виде вектор-столбцов.: - Построить график, подставляя индексные переменные (Рис.3.10).
Можно ввести x и y, как векторы. В этом случае на графике в соответствующих ячейках указываются только имена переменных (Рис.3.11).
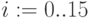 ,
, 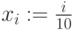 ,
, 
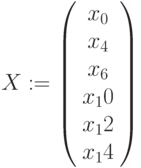
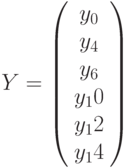
Графики функции, заданной параметрически
В ряде случаев для задания функций используются параметрически заданные уравнения. Например, пусть функции x=x(t), y=y(t), непрерывны при t из (a, b) и устанавливают зависимость (x,y) точки плоскости от значения параметра t. Таким образом, задается на плоскости кривая в параметрической форме. Х=f1(t) и у=f2(t).
Пример 3.5
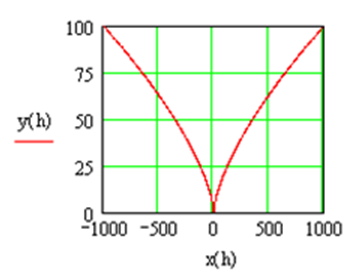
Построить график функции, заданной в виде:
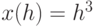
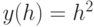 при
при 
В случае построения графика параметрически заданной кривой в шаблоне функции необходимо указать y(h), вместо независимой переменной x под осью абсцисс необходимо соответственно задать x(h) (Рис.3.12).
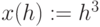 ,
, 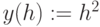 ,
,