Элементы математической статистики
Цель лекции. Показать методику и инструменты MathCAD для работы со случайными величинами.
5.1. Функции для решения задач математической статистики
Случайной величиной (СВ) называется величина, которая в результате опыта может принять только одно из множества значений, причем заранее, до опыта, неизвестно, какое именно. Случайная величина (СВ) может быть дискретной, в этом случае она принимает значение из дискретного числового множества M={1, 2, 3, 4, 5} [10,12]. Случайная величина может быть непрерывной, тогда принимает значения из непрерывного числового множества. Каждая СВ полностью определяется своей функцией распределения. Если X - СВ, возможные значения которой x1,x2,.. Функцией распределения F(x), или интегральным законом распределения, случайной величины X называется зависимость вероятности P выполнения неравенства X < х от возможных значений х
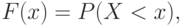 |
( 5.1) |
Функция распределения СВ содержит о ней всю информацию, поэтому важно изучение и исследование функции распределения СВ, которую часто называют просто распределением.
Непрерывную СВ можно также задать, используя другую функцию - плотность распределения или плотность вероятности или дифференциальную функцию.
Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x), являющаяся первой производной от функции распределения F(x) -  .
.
Из определения следует, что функция распределения является первообразной для плотности распределения. Если функция f(x) - плотность распределения непрерывной СВ, то для любых a < b
 |
( 5.2) |
Зная плотность вероятности, можно найти функцию распределения [10,12].
Функции для генерации последовательности случайных величин (СВ) находятся в категории Random numbers; имена функций начинаются на r, далее следует сокращённое название закона, например: - rnd (x) – генерирует одно число, равномерно распределённое от 0 до х; - rnorm (n, m, d) – генерирует n чисел, распределённых по нормальному закону с средним m и среднеквадратичным отклонением 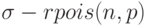 – генерирует n чисел, распределённых по закону Пуассона с параметром р.
– генерирует n чисел, распределённых по закону Пуассона с параметром р.
Функции распределения случайной величины находятся в категории Probaility distribution; имена функций начинаются на p, далее следует сокращённое название закона. Например: 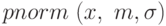 – рассчитывает в точке x значение функции распределения вероятности для нормального закона с средним m и среднеквадратичным отклонением
– рассчитывает в точке x значение функции распределения вероятности для нормального закона с средним m и среднеквадратичным отклонением  ppois (n,p) – рассчитывает в точке x значение функции распределения вероятности для закона Пуассона с параметром p.
ppois (n,p) – рассчитывает в точке x значение функции распределения вероятности для закона Пуассона с параметром p.
Функции плотности распределения случайной величины находятся в категории Probability density; имена функций начинаются на d, далее следует сокращённое название закона. Например: dunif (x, a, b). – значение функции плотности вероятности в точке x для равномерного закона на интервале [a,b], a < b, - dpois (x,p) – значение функции плотности вероятности в точке x для закона Пуассона с параметром p.
Функции для расчёта числовых характеристик случайных величин. При решении практических задач важно числовые параметры СВ - количественные критерии, которые позволяют дать оценку наиболее существенным признакам случайной величины. К таким величинам относятся: математическое ожидание (или среднее), дисперсия, среднеквадратическое отклонение и т.д. [10, 12]. Функции для расчёта числовых характеристик находятся в категории Statistics. Например, mean (v) – среднее значение, var (v)– дисперсия;- stdev (v)– среднеквадратичное отклонение и т.д. Здесь v - вектор значений случайной величины.
Все функции приведены в приложении.
5.2. Генерация случайных чисел
При генерации программа создаёт последовательность псевдослучайных чисел. Псевдослучайные величины вырабатываются алгоритмически и представляют последовательность чисел, обладающих свойствами случайных чисел. Псевдослучайные числа связаны с некоторым задаваемым стартовым значением. Для того, чтобы поменять саму последовательность сгенерированных случайным датчиком чисел, в MathCAD предусмотрена возможность определения начального – стартового значения. В меню Tools/ Worksheet Options (Инструменты/ Опции листа), на вкладке Built-in Variables (Встроенные переменные) в поле ввода Seed value for random устанавливается начальное (стартовое) значение для генератора псевдослучайных чисел. Альтернативный способ: использование встроенной функции seed(x) прямо в документе:
seed(x) — функция установки нового начального значения для генератора псевдослучайных чисел, х — новое начальное значение для генератора псевдослучайных чисел (целое число от 1 до 2147483647) [3, 4].
Равномерное распределение - распределение с постоянной вероятностью
Пример 5.1
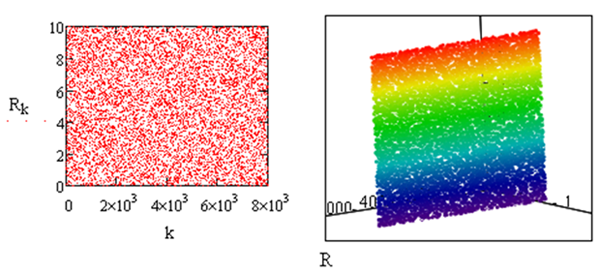
Построим 8000 чисел равномерно распределенной СВ в интервале от 0 до 10 и ее график.
Используем функцию rnd(x) из категории Random numbers.
Функция rnd(x) генерирует равномерно распределенное случайное число между 0 и x . [4, 9].
Для генерации массива используем ранжированную переменную. MathCAD создает массив СВ в виде вектора, значения которого представляются в виде таблицы, 1 столбец которой – номер, 2 столбец - значение случайной величины. Если массив большой, чтобы просмотреть все значения СВ – надо щелкнуть по таблице и использовать линейку прокрутки. Можно представить СВ в виде одномерной индексной переменной. На листинге решения (Рис.5.1) R – вектор случайной величины. График СВ построен на плоскости для индексной переменной и трехмерный для вектора R. Графики построены в виде точек.

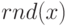 - генерирует одно число, равномерно распределенное от 0 до x.
- генерирует одно число, равномерно распределенное от 0 до x.
 - равномерно распределенное случайное число в интервале [0;2]
- равномерно распределенное случайное число в интервале [0;2]
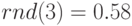 - равномерно распределенное в интервале [0;3]
- равномерно распределенное в интервале [0;3]
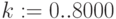

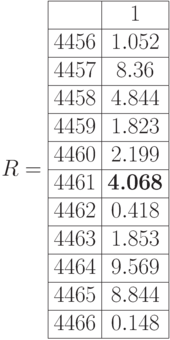
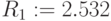


Нормальное распределение
Пример 5.2
Построим 1000 элементов СВ, распределенных по нормальному закону со средним 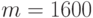 среднеквадратичным отклонением
среднеквадратичным отклонением 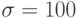 .
.
Для генерации используем функцию rnorm () из категории Random numbers.
Функция 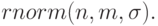 - генерирует вектор n независимых случайных чисел, каждое из которых имеет нормальное распределение с средним m и среднеквадратичным отклонением
- генерирует вектор n независимых случайных чисел, каждое из которых имеет нормальное распределение с средним m и среднеквадратичным отклонением  ;.
;.
Функция rnorm() также создает массив СВ в виде вектора. . На листинге (Рис.5.2) NR – -вектор случайной величины. Как и в примере 5.1. построим график СВ на плоскости для индексной переменной 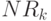 в виде точек и линий и трехмерный точечный для матрицы NR.
в виде точек и линий и трехмерный точечный для матрицы NR.


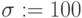
увеличить изображение
Рис. 5.2. Листинг решения примера 5.2. Вектор СВ NR и графики вектора NR .на плоскости и в простанстве
Числовые характеристики
Рассчитаем числовые характеристики СВ: среднее, минимальное, максимальное значение, дисперсию, среднеквадратичное отклонение . Используем функции из категории Statistics.
Числовые характеристики СВ с равномерным распределением для примера 5.1 .
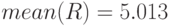 - среднее
- среднее
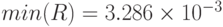 - минимальное
- минимальное
 - максимальное
- максимальное
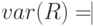 - дисперсия
- дисперсия
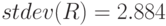 - среднеквадратичное отклонение
- среднеквадратичное отклонение
Числовые характеристики СВ с нормальным распределением для примера 5.2
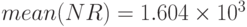 - среднее
- среднее
 - минимальное
- минимальное
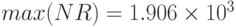 - максимальное
- максимальное
 - дисперсия
- дисперсия
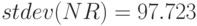 - среднеквадратичное отклонение
- среднеквадратичное отклонение