Проективная геометрия в компьютерном зрении

1.5. Калибрация камеры

Мы обсудили, что у нас есть внутренние параметры камеры – 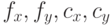– матрица K, и есть коэффициенты дисторсии. И если мы хотим эту математику применять, чтобы понять, куда трехмерные точки переходят – нам нужно эти коэффициенты откуда-то брать. Пока откуда их брать – совершенно непонятно. И чтобы понять, какие у камеры внутренние параметры, какие конкретно у нее коэффициенты, проводится процедура калибрации камеры. Если мы много раз покажем камере объект, про который мы знаем, как он устроен, то мы сможем найти эти параметры.

Рис. 5.10. OpenCV test data

Например, шахматная доска – мы знаем, какие именно у нее точки – мы можем посмотреть, в какие точки они перешли на изображении. Если мы много раз покажем этот шаблон нашей камере и увидим, куда проецируются точки, то мы сможем установить эти параметры. У нас вновь возникает задача оптимизации. Мы знаем трехмерные координаты углов (мы можем измерить размеры квадрата и записать трехмерные координаты шахматной доски), мы можем продетектировать эти уголки на изображении – это стандартная задача. Таким образом, у нас будет соответствие между трехмерной точкой и двухмерной точкой. И нам нужно найти такие параметры, чтобы трехмерные точки переходили именно в эти двухмерные точки. То есть нам нужно оптимизировать параметры камеры так, чтобы у нас получалась правильная проекция. Имеет ли значение положение доски и то, что она расположена перпендикулярно камере? Для калибровки нам нужно показывать доску под разными углами – ее можно поворачивать, ее нужно показать во всех частях камеры для того, чтобы надежно установить ее параметры. Потому что если вы будете показывать шаблон в одной и той же позиции в одном углу, то мы хорошо выясним, как камера проецирует этот угол, но во всей остальной части изображения все может быть очень плохо.

Рис. 5.11. OpenCV test data

Помимо шахматной доски можно использовать и другие шаблоны – например, шаблон из нарисованных кружков, он показывает более точные результаты, потому что центра круга можно найти с большей точностью, чем угол шахматной доски. Соответственно, калибрация получается более точной. Можно использовать более сложные шаблоны, например, трехмерные.

Рассмотрим за счет чего именно происходит калибрация. Допустим, мы поместили в какую-то часть камеры доску. Для шахматной доски мы знаем все углы и все соответствия, у нас здесь задача простая – все соответствия есть и все соответствия правильные. Проекция каждой точки дает нам уравнение, ограничение, как должна проецировать камера. Мы составляем эти ограничения из всех изображений – обычно это несколько десятков – и решаем задачу оптимизации. В обычных условиях достаточно одной калибровки для одной камеры. Предоставляют ли производители камер какие-либо технические данные? Проблема в том, что для одной модели эти параметры будут немножко отличаться. Можно предоставить какие-то параметры по умолчанию и такие камеры существуют, для которых они посчитаны – для модели. Но для конкретной вашей камеры данной модели они могут немного отличаться. Потому что если бы они не отличались, это означало бы, что матрица расположена абсолютно на одном и том же месте, абсолютно такие же линзы. На практике такое невозможно. У вас всегда будут небольшие отклонения, следовательно, ваши параметры калибрации тоже будут немного другими. Поэтому для более точных параметров необходимо делать калибровку самому. Можно пытаться OpenCV test data делать автокалибрацию – снимать камерой обычное изображение – без шаблонов шахматной доски, и при этом пытаться понять, какие у нее внутренние параметры. Автоматически, без шаблонов, пытаться понять, как она искажает. Но на практике получается, что иногда это работает, иногда это не работает. В алгоритме автокалибрации есть несколько параметров – эти параметры нужно подбирать для того, чтобы запустить алгоритм, потому что при одних параметрах алгоритм сработает хорошо, при других сработает плохо. Есть статьи на эту тему о том, как это можно делать. Но пока эта задача не решена. В ситуации же с использованием шаблонов – вы с гораздо большей над?жностью получите хорошую калибрацию камеры.

1.6. Планарные объекты. Гомография

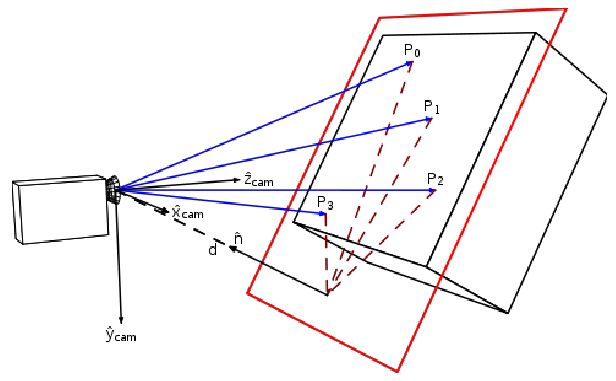
Следующее, что нужно рассмотреть – это работа с планарными (плоскими) объектами. В компьютерном зрении часто возникают планарные объекты – это особый важный случай, который нужно обсудить отдельно, и рассмотреть какие именно преобразования получаются для плоских объектов. Это преобразование называется гомографией. Пусть у нас есть какой-то плоский объект, у него какие-то точки p1,p2,p3,p0 – расположенные в одной плоскости.

Рис. 5.12. Planar object (Homography, Wikipedia)

Мы снимаем их камерой с одной точки, а потом снимаем их камерой с другой позиции. Также можно говорить, что у нас камера фиксирована, и мы снимаем шаблон в одной позе, а потом объект переместился, и мы снимаем его в другой позе. Оказывается, что координаты точек на изображении – на первом и на втором – они будут связаны преобразованиями гомографии:

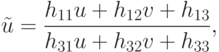
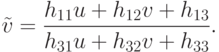
Это преобразование мы сейчас выведем.

Рассмотрим проекцию на первом изображении и проекцию на втором изображении. Во втором случае у нас другая проекционная матрица, потому что поза другая, соответственно точка тоже будет другая. Мы хотим найти преобразование между пикселями на изображении. Идея получения этого преобразования состоит в следующем: так как объект плоский, то мы можем выбрать такую систему координат, в которой начало координат расположено где-то на этой плоскости, ось Z будет направлена по нормали к этой плоскости. И как-то направлены оси X, Y. В этой системе координат будут новые проекционные матрицы, которые всегда можно пересчитать. Главное, что координаты нашего объекта теперь вместо (X,Y,Z,1) будут (X,Y,0,1). При умножении такого вектора (X,Y,0,1) на проекционную матрицу размерности 3*4, то третий столбец будет все время умножаться на ноль. Поэтому на плоскости в качестве проекционной матрицы мы можем использовать матрицу P без третьего столбца и умножать ее на вектор (X,Y,1). Тоже самое верно для второго изображения. Теперь новые проекционные матрицы P1’ и P2’ имеют размерность 3*3, дальнейшее просто. Мы можем слева умножить на обратную матрицу, получим, что

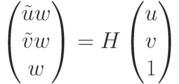
Получается, что если мы знаем координаты первого изображения на плоскости, то существует такая матрица , умножив на которую, мы получим координаты на втором изображении.

Матрица Н и есть преобразование гомографии. Поскольку все происходит в однородных координатах, то можно умножить на любой ненулевой коэффициент w, и все будет тоже самое. Для перехода от однородных координат к пикселям, необходимо поделить на w.

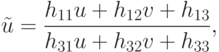
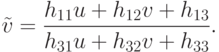
Теперь посмотрим, как матрицу гомографии можно использовать для нахождения плоского объекта на изображении.

У нас есть плоский объект, который мы хотим найти,

Рис. 5.13. OpenCV features2d tutorial

и есть тестовое изображение, на котором он где-то расположен.

Рис. 5.14. OpenCV features2d tutorial

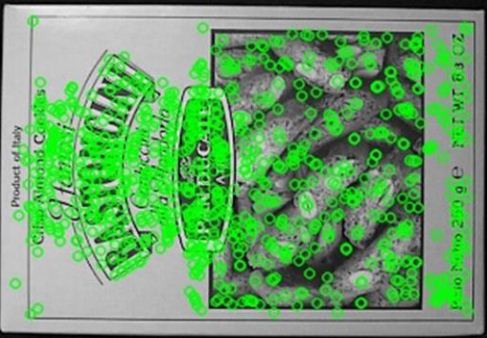
Мы применяем стандартную схему. Мы находим ключевые точки, находим дескрипторы, и мы находим соответствия между дескрипторами.

У нас есть много ложных соответствий, поэтому сразу непонятно, где находится объект.

Рис. 5.15. OpenCV features2d tutorial

Но мы вновь можем применить схему RANSAC. Случайно выберем четыре соответствия, по ним найдем матрицу гомографии. И генерировать до тех пор, пока не получится много инлайеров. И после применения этой схемы мы уже находим искомый объект.

Рис. 5.16. OpenCV features2d tutorial

Это очень мощная идея – геометрическая валидация соответствий. У нас очень много соответствий, но мы знаем, что правильные соответствия переводят плоский объект в плоский объект, поэтому они должны подчиняться гомографии. Таким образом, выкидывая те соответствия, которые не соответствуют гомографии, мы оставляем только правильные и, тем самым, находим объект на изображении.