|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Проективная геометрия в компьютерном зрении
1.2. Pinhole-камера
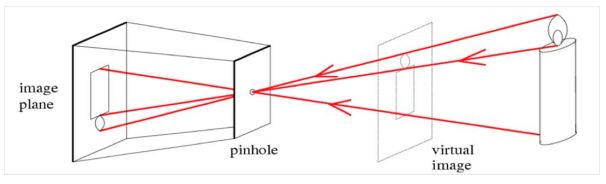
В первую очередь, построим модель: как камера видит трехмерный мир? по каким законам, геометрические структуры, которые в нем есть, проецируются на изображение? Потом мы научимся решать обратную задачу – по данному изображению понять какой трехмерный мир, какая сцена могли его задать. Наиболее популярная модель – это проективная модель камеры, или pinhole-камера (pinhole – булавочное отверстие).
В этой модели камера представляет собой маленькое отверстие, сквозь которое поступает свет. Соответственно, если взять точку наверху свечи, то когда свет поступает через это отверстие, верхняя точка свечи будет проецироваться на изображение уже вниз. Плоскость (image plane) представляет собой матрицу камеры, на которой получается изображение трехмерного мира – фотография. На этой плоскости верх объекта проецируется вниз, а для низа получается наоборот, и объект получается перевернутым. Если смотреть, как именно устроен глаз, то у него такая же модель и в н?м получается проекция перевернутая, а затем мозг уже ее правильно интерпретирует. Кстати говоря, можно провести следующий забавный эксперимент. Существуют специальные очки, надев которые вы будете все видеть в перевернутом виде. Если вы походите в таких очках некоторое время (несколько дней), то ваш мозг приспособиться к этому и будем сам переворачивать картинку обратно – вы в этих очках сможете все нормально делать. Когда вы их снимете, то вам опять будет неудобно, но через какое-то время вы вновь перестроитесь, и все восстановится обратно.
Перейдем теперь к формулам, описывающим преобразование, осуществляемое камерой. Эти формулы самые важные в проективной геометрии, и они будут использоваться на протяжении всего раздела.
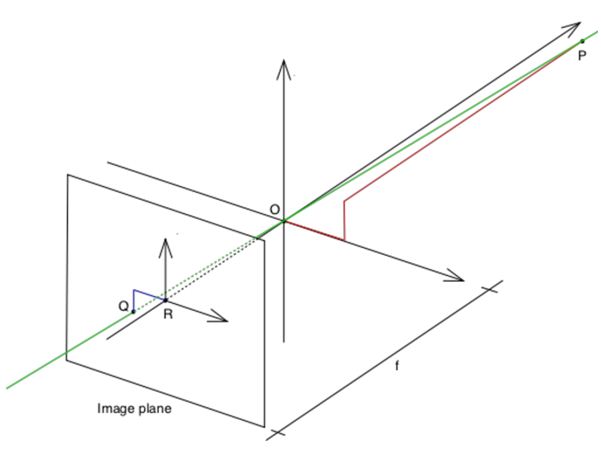
В пространстве введем прямоугольную систему координат (X, Y, Z) следующим образом. Пусть ее начало находится в том самом маленьком отверстии – центре проекции (pinhole). Ось Z направлена по направлению камеры – это так называемая оптическая ось. Оси X и Y можно задавать по-разному. Обычно в математике ось Y направлена вверх, но в компьютерной графике ось Y обычно направлена вниз.
Напомним, что положение жесткого объекта (твердого тела) в пространстве задается 6 параметрами, например, 3 координатами центра масс и 3 эйлеровыми углами, отвечающими за поворот тела вокруг центра масс. Пусть T – центр масс объекта, а R – матрица поворота, которую можно построить по эйлеровым углам. Тогда формула пересчета координат имеет вид
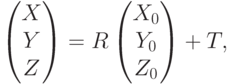
где 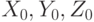 – начальные координаты точки, принадлежащей твердому
телу (в системе координат, связанной с этим объектом), X,Y,Z –
координаты этой точки в текущей сцене. Из подобия треугольников
получаются следующие формулы для координат этой точки на
изображении:
– начальные координаты точки, принадлежащей твердому
телу (в системе координат, связанной с этим объектом), X,Y,Z –
координаты этой точки в текущей сцене. Из подобия треугольников
получаются следующие формулы для координат этой точки на
изображении:
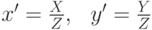
вычисленные в некоторых безразмерных единицах. Чтобы получить
координаты в пикселях, отмасштабируем  и
и 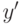 и произведем сдвиг:
и произведем сдвиг:
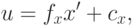
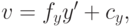
где 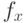 и
и 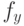 – масштабирующие коэффициенты, а – коэффициенты
сдвига. Заметим, что масштабирующие коэффициенты
– масштабирующие коэффициенты, а – коэффициенты
сдвига. Заметим, что масштабирующие коэффициенты 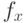 и
и 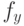 здесь не
обязательно равны, так как пиксели не обязательно квадратные. Смысл
коэффициентов
здесь не
обязательно равны, так как пиксели не обязательно квадратные. Смысл
коэффициентов 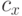 ,
,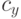 нетрудно понять, если в наши формулы подставить
точку с координатами
нетрудно понять, если в наши формулы подставить
точку с координатами  т. е. точку, находящуюся на
расстоянии от камеры на оптической оси. Легко видеть, что эта точка на
изображении будет иметь координаты
т. е. точку, находящуюся на
расстоянии от камеры на оптической оси. Легко видеть, что эта точка на
изображении будет иметь координаты 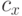 ,
,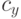 . Таким образом,
. Таким образом, 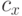 ,
,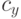 примерно совпадают с координатами центра изображения.
примерно совпадают с координатами центра изображения.
Приведенные формулы удобнее записывать в однородных координатах:
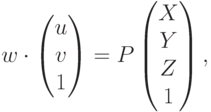
где
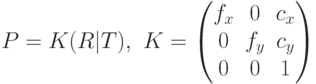
Матрица имеет размеры  и называется проекционной матрицей. Она
получается как произведение матрицы K, содержащей внутренние
параметры камеры, и матрицы
и называется проекционной матрицей. Она
получается как произведение матрицы K, содержащей внутренние
параметры камеры, и матрицы 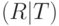 , полученной приписыванием к
матрице R вектора сдвига t.
, полученной приписыванием к
матрице R вектора сдвига t.
Особенность однородных координат заключается в том, что умножение их на одно и то же число, приводит, по существу, к той же точке – мы можем умножать координаты на любое число Поэтому для получения непосредственно координат в пикселях, необходимо поделить полученный вектор на такую величину, чтобы последняя координата была равна 1.
Однородные координаты возникают здесь очень естественным путем.
Рассмотрим точку  на изображении. В нее проецируются все точки
некоего луча. Таким образом, с точки зрения проекции все точки на луче
для нас одинаковые. Например, это так для точек (X,Y,Z), 2(X,Y,Z), 1/2(X,Y,Z) и т. д. – для всех точек, полученных умножением (X,Y,Z) на
ненулевой скаляр.
на изображении. В нее проецируются все точки
некоего луча. Таким образом, с точки зрения проекции все точки на луче
для нас одинаковые. Например, это так для точек (X,Y,Z), 2(X,Y,Z), 1/2(X,Y,Z) и т. д. – для всех точек, полученных умножением (X,Y,Z) на
ненулевой скаляр.
Рассмотрим, как используются эти формулы на практике. Мы построили матрицу P , и хотим узнать в какой пиксель перешла точка (X,Y,Z,1). Умножаем координаты точки на P – получаем вектор в однородных координатах и нормируем его, таким образом, чтобы последняя координата была равна 1. Получившиеся первые две координаты – это уже конкретные координаты в пикселях на изображении.

 "
"