|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2.? |
Отношения
Основные понятия отношений
Часто в вычислениях необходимо выбирать элементы множеств, которые удовлетворяют некоторому " отношению ". Это понятие довольно общее, поэтому широко применимо. При соответствующем выборе отношения его аргументы могут быть связаны какой-либо формулой, иногда достаточно простой, если возможно найти удачное описание.
Рассмотрим пример, иллюстрирующий понятие отношения ( рис. 3.1):
Предположим, что  - множество программ;
- множество программ;  - конечное множество данных;
- конечное множество данных;  - множество результатов.
- множество результатов.
Если мы выберем конкретное значение из  , то оно может использоваться в некоторых программах из
, то оно может использоваться в некоторых программах из  и для каждой программы из
и для каждой программы из  существует совокупность значений из
существует совокупность значений из  , которые в ней используются. Таким образом, мы имеем соответствие между значениями данных и программами, и, следовательно, существуют элементы
, которые в ней используются. Таким образом, мы имеем соответствие между значениями данных и программами, и, следовательно, существуют элементы  , представляющие интерес. Аналогично, если мы сведем рассмотрение к
, представляющие интерес. Аналогично, если мы сведем рассмотрение к 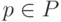 , то
, то  связывает соответствующие данные из
связывает соответствующие данные из  с результатами из
с результатами из  .
.
Можно рассматривать данные, приводящие к остановке, или результаты, которые не могут быть получены из  . Следовательно, мы приходим к подмножеству
. Следовательно, мы приходим к подмножеству  .
.
Определение.  -местным отношением
-местным отношением  на множествах
на множествах  называется подмножество прямого произведения
называется подмножество прямого произведения 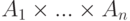 .
.
Другими словами, элементы 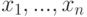 (где
(где 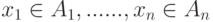 ) связаны отношением
) связаны отношением  тогда и только тогда, когда
тогда и только тогда, когда 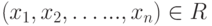 , а (
, а (  ) - упорядоченный набор из
) - упорядоченный набор из  элементов.
элементов.
Наиболее часто встречаются отношения при 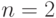 ; в этом случае они называются бинарными отношениями. Следовательно, бинарные отношения между множествами
; в этом случае они называются бинарными отношениями. Следовательно, бинарные отношения между множествами  и
и  являются просто подмножеством
являются просто подмножеством  . Если эти множества эквивалентны (скажем, равны
. Если эти множества эквивалентны (скажем, равны  ), то будем говорить, что подмножество
), то будем говорить, что подмножество 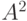 определяет отношения на
определяет отношения на  .
.
Отношения не являются чем-то новым. Можно построить отношения, которые несомненно будут знакомы вам.
Пример 1. Пусть 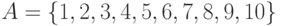 .
.
Тогда  .
.
В явном виде
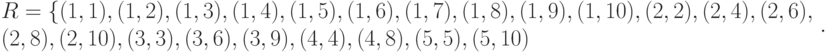
Пример 2 (шахматы). Пусть 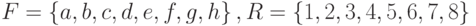 и пусть
и пусть 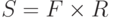 .
.
Таким образом,  - множество всех клеток, обозначаемых парами
- множество всех клеток, обозначаемых парами  , где
, где 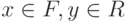 .
.
Определим бинарное отношение  для ладьи на множестве
для ладьи на множестве  так, что
так, что 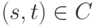 тогда и только тогда, когда
тогда и только тогда, когда  и
и  - элементы
- элементы  и ладья может пройти от
и ладья может пройти от  к
к  одним ходом на пустой доске.
одним ходом на пустой доске.
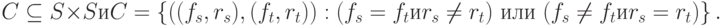
Напомним, что ладья может изменять либо горизонтальную координату, либо вертикальную, но не обе одновременно.
В общем случае ряд различных отношений на множестве  зависит от
зависит от  . Большая часть этих отношений не представляет интереса, но отдельные оказываются полезными.
. Большая часть этих отношений не представляет интереса, но отдельные оказываются полезными.
Определение 1. Для любого множества  определим тождественное отношение
определим тождественное отношение  и универсальное отношение
и универсальное отношение  следующим образом:
следующим образом:
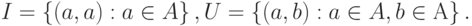
Таким образом,  . Так как
. Так как 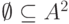 , то
, то  является отношением на
является отношением на  и называется пустым отношением.
и называется пустым отношением.
Пусть отношение  определено в соответствии с изображением на
рис.
3.2. Свяжем с каждым бинарным отношением
определено в соответствии с изображением на
рис.
3.2. Свяжем с каждым бинарным отношением  между
между  и
и  - область определения
- область определения  и область значений
и область значений 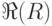 . Они определяются следующим образом.
. Они определяются следующим образом.
Определение 2. Область определения - это множество значений  , таких, что пара
, таких, что пара  принадлежит отношению
принадлежит отношению  , а область значений
, а область значений 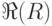 это множество значений
это множество значений  , таких, что пара
, таких, что пара  принадлежит отношению
принадлежит отношению 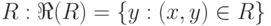 .
.
Пример 3. Пусть отношение  такое же, как и в примере 1,
такое же, как и в примере 1,  . В явном виде
. В явном виде 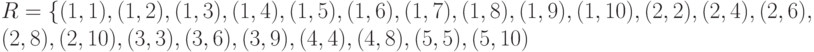 .
.
Тогда 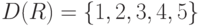 , т. е.
, т. е. 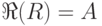 .
.
Хотя каждое отношение является множеством и может быть обозначено прописной буквой, иногда отношения обозначаются строчными греческими буквами: 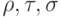 .
.
Например:
a) 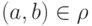 , т. е.
, т. е. 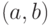 находится в
находится в  ;
;
б) 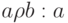 связано с
связано с  отношением
отношением  ;
;
в)  .
.
Определение 3. Пусть  - бинарное отношение. Определим обратное отношение
- бинарное отношение. Определим обратное отношение 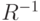 следующим образом:
следующим образом:

Таким образом, 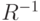 связывает те же пары элементов, что и
связывает те же пары элементов, что и  , но "в другом порядке". Следовательно, если
, но "в другом порядке". Следовательно, если 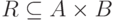 , то
, то 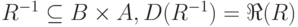 и
и 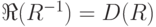 .
.
Можно  писать
писать 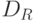 и
и 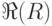 как
как  .
.



