|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Пути и циклы в графах
Орциклы и циклы
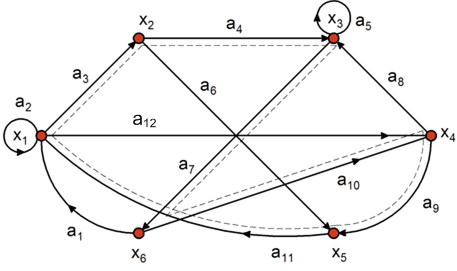
Особую группу составляют замкнутые пути. Путь a1, a2, ...,aq называется замкнутым, если в нем начальная вершина a1 и конечная вершина aq совпадают. Так, например, для графа на рис. 8.3 можно составить несколько замкнутых путей:
М1: a3, a6, a11,
М2: a11, a3, a4, a7, a1, a12, a9,
М3: a3, a4, a7, a10, a9, a11.
Пути М1 и М3 являются замкнутыми простыми орцепями, называемыми контурами или простыми орциклами, поскольку в них одна и та же вершина используется только один раз (за исключением начальной и конечной). Путь М2 не является контуром, так как вершина х1 используется в нем дважды.
Контур, проходящий через все вершины графа, имеет особое название – гамильтонов контур. Путь М3 является гамильтоновым контуром. Он показан штриховой линией на рис. 8.3.
Для неориентированного графа замкнутым маршрутом является неориентированный двойник замкнутого пути, т. е. замкнутым маршрутом является маршрут, в котором совпадают начальные и конечные вершины.
Для неориентированного графа понятия цикла и гамильтонова цикла аналогичны понятиям орцикла и гамильтонова контура в орграфе.
Эйлеровым циклом в графе называется цикл, содержащий все ребра графа. Граф, содержащий эйлеров цикл, называется эйлеровым графом.
Эйлеровым путем в графе называется путь, содержащий все ребра графа по одному разу. Граф, содержащий эйлеров путь, называется полуэйлеровым графом.
ТЕОРЕМА. Связный неориентированный граф G содержит эйлеров цикл тогда и только тогда, когда число вершин нечетной степени равно нулю 0.
ТЕОРЕМА. Связный неориентированный граф G содержит эйлеров путь тогда и только тогда, когда число вершин нечетной степени равно нулю 0 или 2.
Эйлер первым в своей знаменитой задаче о Кенигсбергских мостах поставил вопрос о существование такого цикла.
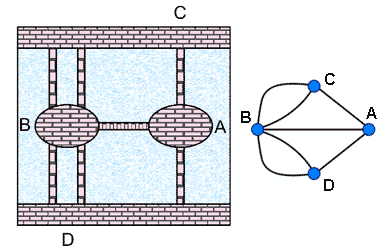
На реке Преголя в Кенигсберге было два острова. Они соединялись между собой и с берегами реки семью мостами, как схематично показано на рис. 8.4. Задача заключалась в том, чтобы за одну прогулку обойти все семь мостов, проходя по каждому мосту только один раз, и вернуться в исходное место.
Если каждый берег реки и острова считать вершинами графа, а каждый мост – ребром, то карту рис. 8.4,а можно представить в виде графа на рис. рис. 8.4,б и ответ на поставленный вопрос зависит теперь от существования эйлерова цикла в этом графе. Эйлер установил, что указанный граф не содержит эйлерова цикла, и этот результат ознаменовал рождение теории графов.