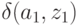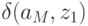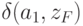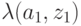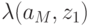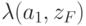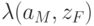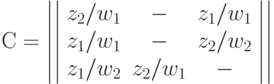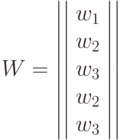Основные понятия теории абстрактных автоматов
1.2. Методы задания автоматов
Для задания конечного автомата S требуется описать все элементы множества
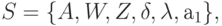
наиболее часто используемой формой описания элементов множества S используется табличный, графический, матричный способы.
Теоретико-множественное представление автоматов.
Для задания конечного автомата 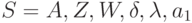 все элементы множества должны быть заданы явно. Так для автомата Мили:
все элементы множества должны быть заданы явно. Так для автомата Мили:
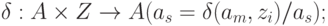
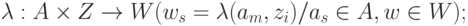
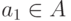 - начальное состояние автомата.
- начальное состояние автомата.
Например, автомат Мили 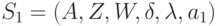 , представленный в табл.1.3 в явной форме описывается так:
, представленный в табл.1.3 в явной форме описывается так:
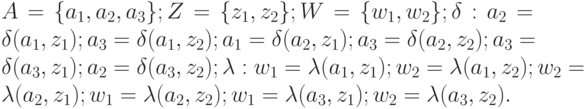
Автомат Мура 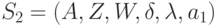 , представленный в табл.1.8 в явной форме описывается так:
, представленный в табл.1.8 в явной форме описывается так:
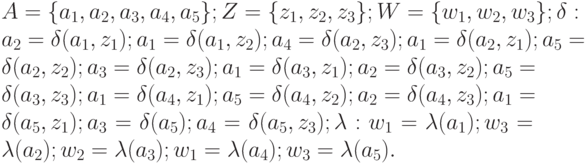
Табличная форма.
Табличная форма для автомата Мили иллюстрируется табл.1.1 (переходов) и табл.1.2 (выходов).
Строки этих таблиц соответствуют входным сигналам, а столбцы - состояниям, причем крайний левый столбец обозначен начальным состоянием 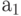 . На пересечении столбца
. На пересечении столбца 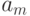 и строки
и строки 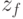 …. в таблице переходов ставится функция перехода
…. в таблице переходов ставится функция перехода 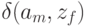 , то есть состояние, в которое автомат переходит из состояния
, то есть состояние, в которое автомат переходит из состояния 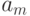 под действием входного сигнала
под действием входного сигнала 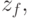 а в таблице выходов - выходная функция
а в таблице выходов - выходная функция 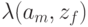 , то есть соответствующий этому переходу выходной сигнал
, то есть соответствующий этому переходу выходной сигнал 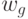 .
.
Пример табличного способа задания автомата Мили показан в табл. 1.3 (переходов) и табл. 1.4 (выходов).
Автомат называется частично заданным, если он определен не для всех пар переходов (  ). Для частично заданного автомата на месте отсутствующего перехода ставится прочерк как в таблице переходов, так и в таблице выходов.
). Для частично заданного автомата на месте отсутствующего перехода ставится прочерк как в таблице переходов, так и в таблице выходов.
Пример табличного способа задания частичного автомата показан в табл.1.5 (переходов) и табл.1.6 (выходов).
Табличная форма задания автомата Мура представляет собой совмещенную табл.1.7, в которой выходной сигнал, соответствующий состоянию в 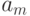 автомате Мура размещен в верхней строке над соответствующими состоянием, а остальная информация аналогична представлению автомата Мили.
автомате Мура размещен в верхней строке над соответствующими состоянием, а остальная информация аналогична представлению автомата Мили.
Пример представления автомата Мура приведен в табл.1.8.
| \ wG | w1 | w3 | w2 | w1 | w3 |
|---|---|---|---|---|---|
| zf\ am | a 1 | a2 | a3 | a4 | a5 |
| z1 | a2 | a1 | a1 | a1 | a1 |
| z2 | a3 | a5 | a2 | a5 | a3 |
| z3 | a4 | a3 | a5 | a2 | a4 |
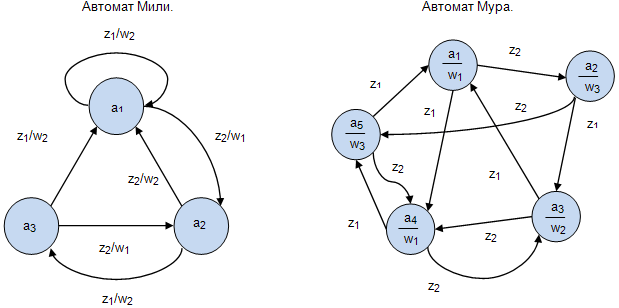
Графовая форма задания абстрактных автоматов
В данном случае автомат  представляется графом, в котором:
представляется графом, в котором:
- множество
 изображено вершинами графа;
изображено вершинами графа; - функция
 задана дугами графа, причем две вершины графа
задана дугами графа, причем две вершины графа 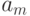 и
и 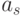 , соединяются дугой, если в автомате существует переход из
, соединяются дугой, если в автомате существует переход из 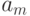 в
в 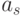 ;
; - множество
 изображено метками дуг:
изображено метками дуг: 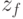 ставится на дуге из вершины
ставится на дуге из вершины 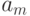 в вершину
в вершину 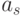 , если в автомате существует переход из
, если в автомате существует переход из 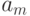 в
в 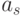 под действием входного сигнала
под действием входного сигнала 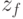 ;
; - функция
 задана метками дуг или вершин: для автомата Мили дуга из вершины
задана метками дуг или вершин: для автомата Мили дуга из вершины 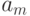 в вершину
в вершину 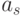 помечается выходным сигналом
помечается выходным сигналом 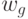 , если в автомате существует переход из
, если в автомате существует переход из 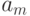 в
в 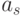 и при этом вырабатывается выходной сигнал
и при этом вырабатывается выходной сигнал 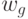 ; а для автомата Мура выходным сигналом
; а для автомата Мура выходным сигналом 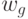 помечается вершина, определяющая
помечается вершина, определяющая  .
.
На рисунке 1.8 приведены примеры описания автомата Мили и автомата Мура:
Матричная форма
Для автомата Мили матричная форма состоит из матрицы 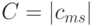 размерностью
размерностью  , где каждый элемент матрицы
, где каждый элемент матрицы 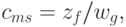 стоящий на пересечении
стоящий на пересечении  -ой строки и
-ой строки и  -го столбца соответствует входному сигналу
-го столбца соответствует входному сигналу 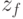 , вызывающему переход из состояния
, вызывающему переход из состояния 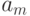 в состояние
в состояние 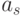 с выработкой выходного сигнала
с выработкой выходного сигнала 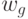 . Пример матричного описания автомата Мили показан ниже.
. Пример матричного описания автомата Мили показан ниже.
Для автомата Мура матричная форма состоит из матрицы 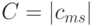 размерностью
размерностью  , где каждый элемент матрицы
, где каждый элемент матрицы 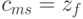 , стоящий на пересечении
, стоящий на пересечении  -ой строки и
-ой строки и  -го столбца, соответствует входному сигналу
-го столбца, соответствует входному сигналу 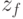 , вызывающему переход из состояния
, вызывающему переход из состояния 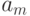 в состояние
в состояние 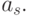 Так как выходной сигнал
Так как выходной сигнал 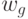 . в автомате Мура зависит только от состояния, следовательно, выходные сигналы могут быть представлены матрицей-столбцом. Пример матричного описания автомата Мура показан на формуле, приведенной выше.
. в автомате Мура зависит только от состояния, следовательно, выходные сигналы могут быть представлены матрицей-столбцом. Пример матричного описания автомата Мура показан на формуле, приведенной выше.

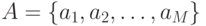 -
- 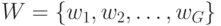 - выходной
- выходной 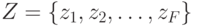 -
-