Основные понятия теории абстрактных автоматов

Введение

"Теория автоматов" - является одной из важных компонент федерального государственного стандарта по направлению "Информатика и вычислительная техника".

Теория автоматов имеет широкие возможности применения:

• Проектирование систем логического управления;
• Обработка текстов и построение компиляторов;
• Спецификация и верификация систем взаимодействующих процессов;
• Языки описания документов и объектно-ориентированных программ;
• Оптимизация логических программ др.

Об этом можно судить по выступлениям на семинаре "Software 2000…" ученых и специалистов.

Дуг Росс: "…80 или даже 90 % информатики (Computer Science) будет в будущем основываться на теории конечных автоматов…"

Herver Gallaire: "Я знаю людей из "Боинга", занимающихся системами стабилизации самолетов с использованием чистой теории автоматов. Даже трудно себе представить, что им удалось с помощью этой теории. "

Brian Randell : "Большая часть теории автоматов была успешно использована в системных программах и текстовых фильтрах в ОС UNIX. Это позволяет множеству людей работать на высоком уровне и разрабатывать очень эффективные программы".

1.1. Основные понятия и определения.

Простейший преобразователь информации (рис.1.1,а) отображает некоторое множество элементов информации Х, поступающее на вход, в некоторое множество на выходе Y. Если множества Х и Y являются конечными и дискретными, то есть преобразование осуществляется в дискретные моменты времени, то такие преобразователи информации называются конечными преобразователями. Элементы множеств Х и Y в этом случае предварительно кодируют двоичными кодами и строят преобразование одного множества в другое.

Результат преобразования 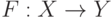зачастую зависит не только от того, какая информация в данный момент появилась на входе, но и от того, что происходило раньше, то есть от предыстории преобразования. Например, один и тот же вход - извинение соседа после того, как он вам наступил на ногу в переполненном автобусе - вызовет у вас одну реакцию в первый раз и совсем другую - в пятый раз.

Рис. 1.1.

Таким образом, существуют более сложные преобразователи информации (ПИ), реакция которых зависит не только от входных сигналов в данный момент, но и от того, что было раньше, от входной истории. Такие ПИ называются автоматами (схемами с памятью). В этом случае говорят об автоматном преобразовании информации (рис.1.1,б). На один и тот же входной сигнал автомат может реагировать по-разному, в зависимости от состояния, в котором он находился. Автомат меняет свое состояние с каждым входным сигналом.

Рассмотрим несколько примеров.

Пример 1^{1Карпов Ю.Г. Теория автоматов-СПб.:Питер, 2003} . Автомат, описывающий поведение "умного" отца.

Опишем поведение отца, сын которого учится в школе и приносит двойки и пятерки. Отец не хочет хвататься за ремень каждый раз, как только сын получит двойку, и выбирает более тонкую тактику воспитания. Зададим такой автомат графом, в котором вершины соответствуют состояниям, а дуга из состояния s в состояние q, помеченное x/y, проводится тогда, когда автомат из состояния s под воздействием входного сигнала х переходит в состояние q с выходной реакцией y. Граф автомата, моделирующего умное поведение родителя, представлен на рис.1.2. Этот автомат имеет четыре состояния 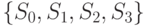, два входных сигнала - оценки 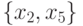и выходные сигналы 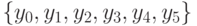, которые будем интерпретировать как действия родителя следующим образом:

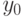- брать ремень;

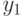- ругать сына;

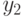- успокаивать сына;

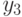- надеяться;

- радоваться;

- ликовать.

Рис. 1.2.

Сына, получившего одну и ту же оценку - двойку, ожидает дома совершенно различная реакция отца в зависимости от предыстории его учебы. Например, после третьей двойки в истории сына встретят ремнем, а в истории будут успокаивать и т.д.

Конечный автомат может быть реализован как программно, так и аппаратно. Программную реализацию можно выполнить на любом языке высокого уровня разными способами. На рис.1.3 представлена блок-схема программы, реализующей поведение автомата примера 1. Нетрудно увидеть, что топология блок-схемы программы повторяет топологию графа переходов автомата. С каждым состоянием связана операция NEXT, выполняющая функцию ожидания очередного события прихода нового входного сигнала и чтения его в некоторый стандартный буфер х, а также последующий анализ того, какой это сигнал. В зависимости от того, какой сигнал пришел на вход, выполняется та или иная функция 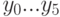и происходит переход к новому состоянию.

Рис. 1.3.

Аппаратную реализацию автомата рассмотрим во второй части этого раздела.

Пример 2. "Студент"

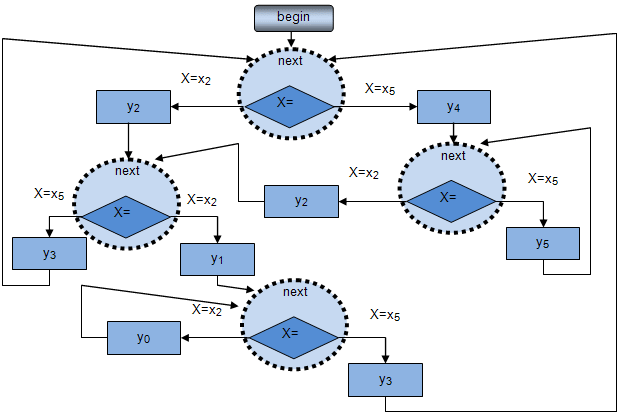
Автомат, модель которого представлена на рис.1.4, описывает поведение студента и преподавателей.

Рис. 1.4.

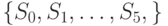- состояния;

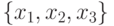- входные сигналы: "н", "2" и "5".

- выходные реакции:

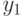• - отмечаем "н";
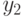• - успокаивать;
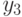• - хвалим студента;
• - поощряем;
• - надеемся;
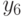• - предупреждаем;
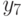• - отчисляем;

Пример 3¹. Электронные часы (рис.1.5).

Электронные часы разнообразных функциональных возможностей являются одним из наиболее широко применяемых в быту электронных приборов, управление которыми построено на основе конечноавтоматной модели. Они обычно показывают: время, дату; у них имеется функции такие как "установка времени и даты", "Секундомер", "Будильник"и т.п. Упрощенная структурная схема электронных часов показана нарис.1.5

Рис. 1.5.

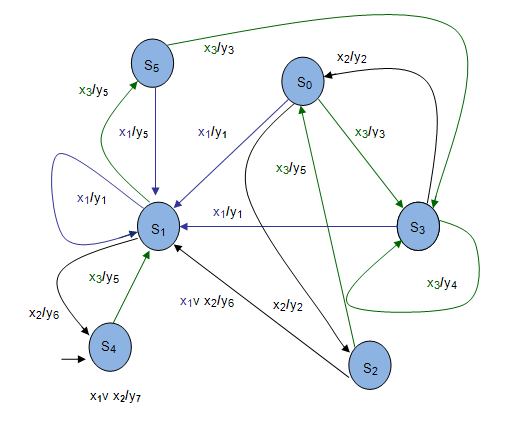
Регистры отображают либо время, либо дату, либо секундомер в зависимости от "Управления". Устройство управления построено на основе модели конечного автомата. Конечный автомат реагирует на нажатия кнопки "а" на корпусе переходом в состояние "Установка минут", в котором событие нажатия кнопки "b" вызовет увеличение числа. Устройство управления построено на основе модели конечного автомата, граф которого показан нарис.1.6

Рис. 1.6.

Итак. С одной стороны АВТОМАТ - устройство, выполняющее некоторые действия без участия человека. С другой стороны, АВТОМАТ - математическая модель, описывающая поведение технического устройства. В данном случае реальное устройство, система и т.д. рассматривается как некоторый "ЧЁРНЫЙ ЯЩИК" (рис.1.7).

Рис. 1.7.

Абстрактный автомат - это математическая модель, описывающая техническое устройство совокупностью входных, выходных сигналов и состояний, кроме того:

• имеет множество внутренних состояний 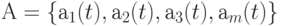, называемых состояниями автомата;
• на вход автомата поступает конечное множество входных сигналов 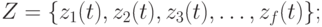имеется конечное множество выходных сигналов ;
• задана функция перехода ;
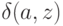• задана функция формирования выходов автомата ;
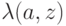• определено начальное состояние автомата .

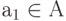То есть для описания автомата нужно использовать шестёрку вида 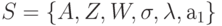, где

• 
• 
• 
• 
• 
• .

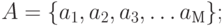
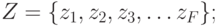
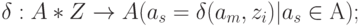
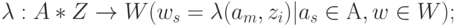
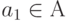Автомат реализует некоторое отображение множества слов входного алфавита Z в множество слов выходного алфавита W.

Автомат называется конечным, если множество его внутренних состояний и множество значений входных сигналов есть конечные множества.

Автомат называется синхронным, если интервал временной дискретизации постоянен, в противном случае говорят об асинхронном автомате.

Автомат называется детерминированным, если поведение автомата в каждый момент времени однозначно определено ( ,)

В зависимости от способа определения выходного сигнала в синхронных автоматах различают:

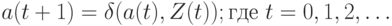
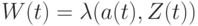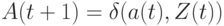1. Автомат первого рода ( Автомат Мили )
   • 
   • ;
2. Автомат второго рода ( Автомат Мура )
   • ,
   • 
   •