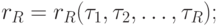НОУ ИНТУИТ | Введение в теорию автоматов. Лекция 5: Синтез структурного автомата

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Вятский государственный университет

Опубликован: 24.04.2008 | Доступ: свободный | Студентов: 2134 / 435 | Оценка: 3.44 / 3.17 | Длительность: 06:01:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Математик

|

Вам нравится? Нравится 30 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматривается структурный автомат. Дается метод канонического синтеза структурных автоматов.

Ключевые слова: микропрограмма, автомат, граф, функциональная схема, представление, вектор, совмещенный автомат, абстрактный автомат, входной, канонический метод синтеза, комбинационная схема, структурная схема, автомат Мили, автомат Мура

5.1 Структурный автомат

Процесс абстрактного проектирования заключается в переходе от исходной микропрограммы (или набора микропрограмм) к одной из традиционных форм задания автомата: матричной, табличной или графической (графу). Этап перехода к заданию автомата также является необходимым, т.к. обеспечивает реализацию процесса структурного проектирования путем использования достаточно, эффективного аппарата теории конечных автоматов.

Структурное проектирование представляет собой процесс перехода от указанных выше форм задания к его функциональной схеме.

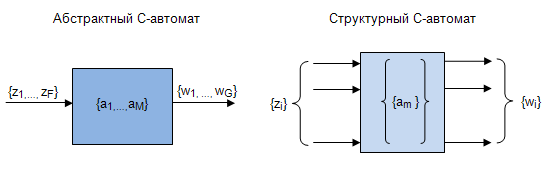
Итак, абстрактный автомат на входе имеет некоторую последовательность входных сигналов, в зависимости от которых переходит из одного состояния в другое, выдавая некоторую последовательность выходных сигналов (рис.5.1).

Рис. 5.1.

В структурном автомате учитывается структура входных и выходных сигналов, то есть их конкретное представление в виде двоичных векторов. Состояния автомата так же кодируются двоичными векторами.

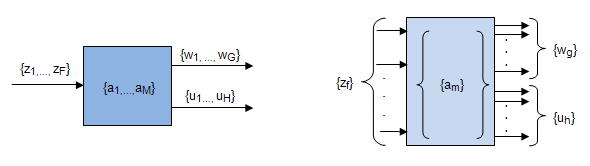
Рассмотрим совмещенный автомат (рис.5.2). Каждое состояние 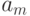a_m абстрактного автомата кодируется двоичным вектором:

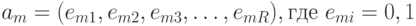$a_m=(e_{m1}, e_{m2}, e_{m3} , \dots , e_{mR}), где\ e_{mi} ={0, 1}$ ,

$R>=]Log2M[, скобки ] и [ показывают,\ что\ берется\ наибольшее\ целое$ ;

- число состояний абстрактного автомата;

- число элементов памяти.

Рис. 5.2.

Входной и выходные сигналы представляются также двоичными векторами:

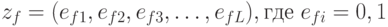$z_f=(e_{f1}, e_{f2}, e_{f3} , \dots , e_{fL}), где\ e_{fi} ={0, 1}$ , , - число входных сигналов абстрактного автомата, - число входов структурного автомата ;
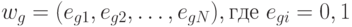$w_g=(e_{g1}, e_{g2}, \dots , e_{gN}), где\ e_{gi} ={0, 1}$ , - число выходных сигналов 1 типа, -число выходов 1 типа структурного автомата ;
$u_h=(e_{f1}, e_{f2}, e_{f3} , \dots , e_{fD}), где\ e_{fi}={0, 1}$ , - число выходных сигналов 2 типа, - число выходов 2 типа структурного автомата

5.2 Канонический метод структурного синтеза автоматов

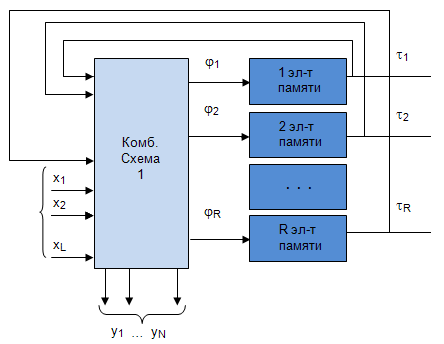
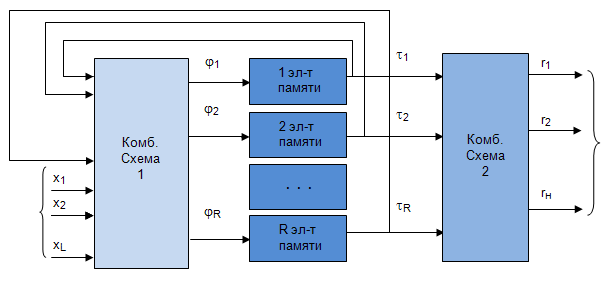
Схема структурного -автомата при каноническом методе синтеза представляется, состоящей из трех частей: двух комбинационных схем и памяти автомата (рис.5.3). Комбинационная схема 1 предназначена для формирования функций возбуждения 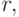поступающих на входы элементов памяти, и выходных сигналов 1 типа 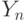Y_n , зависящих от входных сигналов 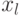x_l и сигналов с выходов элементов памяти .

Рис. 5.3.

Комбинационная схема 2 предназначена для формирования выходных сигналов 2 типа r_h как функций с выходов элементов памяти .

Так как в автомате Мили сигналы 2 типа отсутствуют, то, соответственно в структурной схеме отсутствует комбинационная схема 2. Схема структурного автомата Мили показана на рис.5.4.

Рис. 5.4.

В автомате Мура сигналы 1 типа отсутствуют, следовательно, в структурной схеме в комбинационной схеме 1 отсутствуют выходные сигналы 1 типа 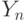Y_n . Схема структурного автомата Мура показана на рис.5.5.

Рис. 5.5.

Таким образом для того, чтобы синтезировать структурный автомат, необходимо синтезировать две комбинационные схемы по системе канонических уравнений. Система канонических уравнений для -автомата выглядит следующим образом:
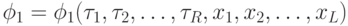
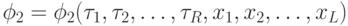
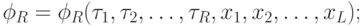
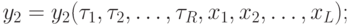
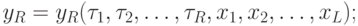
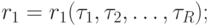
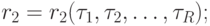