Оценивание тестирования
Задача 2.
Даны результаты тестирования для каждого из n тестированных и теста длины  в виде матрицы
в виде матрицы  , а также вектор эталонных ответов
, а также вектор эталонных ответов 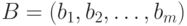 , где
, где  – эталонный ответ на задание номер
– эталонный ответ на задание номер  . Необходимо определить "вес" (меру сложности) конкретного задания теста.
. Необходимо определить "вес" (меру сложности) конкретного задания теста.
Простейший алгоритм решения этой задачи состоит из следующих этапов.
- Определяем для очередного задания теста по матрице
 количество тестированных, давших правильный ответ на данное задание.
количество тестированных, давших правильный ответ на данное задание. - В качестве "веса" задания берется дробь
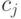 : знаменатель – количество тестированных, числитель – количество тестированных, давших правильные ответы на все задания.
: знаменатель – количество тестированных, числитель – количество тестированных, давших правильные ответы на все задания. - Вычисляем смежные веса
 : знаменатель – количество всех тестированных, давших неправильный ответ на данное задание номер
: знаменатель – количество всех тестированных, давших неправильный ответ на данное задание номер  , числитель – количество тестированных, давших неправильные ответы на все задания. Иногда в знаменателе берется количество всех тестированных.
, числитель – количество тестированных, давших неправильные ответы на все задания. Иногда в знаменателе берется количество всех тестированных. - Находится вектор весов выполнения
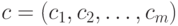 для заданного вектора
для заданного вектора  эталонных ответов.
эталонных ответов. - Находим вектор весов невыполнения
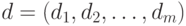 для заданного вектора
для заданного вектора  эталонных ответов.
эталонных ответов. - Оцениваем дисперсию каждого
 -го задания
-го задания 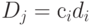 и стандартное отклонение
и стандартное отклонение 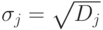 .
. - Конец алгоритма.
Задача 3.
Даны результаты тестирования для каждого из  тестированных и теста длины
тестированных и теста длины  в виде матрицы
в виде матрицы  , а также вектор эталонных ответов
, а также вектор эталонных ответов 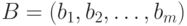 , где
, где  – эталонный ответ на задание номер
– эталонный ответ на задание номер  . Необходимо оценить валидность каждого задания теста.
. Необходимо оценить валидность каждого задания теста.
Простейший алгоритм решения этой задачи состоит из следующих этапов.
- Определяем для очередного задания теста по матрице
 количество тестированных, давших правильный ответ на
количество тестированных, давших правильный ответ на  -ое задание и находим их средний балл
-ое задание и находим их средний балл  .
. - Находим аналогично количество тестированных, давших неправильный ответ на j-ое задание и их средний балл
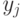 .
. - Находим дробь
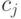 : знаменатель – количество тестированных, давших правильный ответ на данное задание номер
: знаменатель – количество тестированных, давших правильный ответ на данное задание номер  , числитель – количество тестированных.
, числитель – количество тестированных. - Находим дробь
 : знаменатель – количество тестированных, давших неправильный ответ на данное задание номер
: знаменатель – количество тестированных, давших неправильный ответ на данное задание номер  , числитель – количество тестированных.
, числитель – количество тестированных. - Оцениваем дисперсию каждого
 -го задания
-го задания 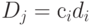 и стандартное отклонение
и стандартное отклонение 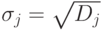 .
. - Находим стандартное отклонение
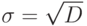 по всему тесту.
по всему тесту. - Находим коэффициент корреляции (меру валидности задания):

- Если
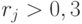 , то задание считаем валидным, иначе – не валидным (отметим, что с точки зрения критериальной валидности, задания, выполненные всеми или невыполненные никем, не являются валидными).
, то задание считаем валидным, иначе – не валидным (отметим, что с точки зрения критериальной валидности, задания, выполненные всеми или невыполненные никем, не являются валидными). - Конец алгоритма.
Задача 4.
Даны результаты нормативно-ориентированного тестирования для каждого из  тестированных и теста длины
тестированных и теста длины  в виде матрицы
в виде матрицы  , а также вектор эталонных ответов
, а также вектор эталонных ответов 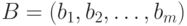 , где
, где  – эталонный ответ на задание номер
– эталонный ответ на задание номер  . Необходимо оценить надежность теста (степень устойчивости результатов тестирования каждого испытуемого, если тестирование было проведено в совершенно одинаковых условиях).
. Необходимо оценить надежность теста (степень устойчивости результатов тестирования каждого испытуемого, если тестирование было проведено в совершенно одинаковых условиях).
Для вычисления надежности нормативно-ориентированного теста используем коэффициент корреляции между результатами двух параллельных тестов. Сравнивая коэффициенты корреляции, делаем заключение о надежности (внутренней) теста. Если две половины теста коррелированны, то и тест надёжен; в противном случае – не надёжен (или необходимо применить другой, более тонкий математический аппарат исследования надежности).
Простейший алгоритм решения этой задачи состоит из следующих этапов.
- Делим тест на две равные части
 и
и  , например, по четным и нечетным номерам заданий. Этот метод называется методом расщепления теста. Таким образом, мы имеем данные по двум параллельным тестам
, например, по четным и нечетным номерам заданий. Этот метод называется методом расщепления теста. Таким образом, мы имеем данные по двум параллельным тестам  и
и  – индивидуальные баллы
– индивидуальные баллы 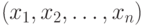 ,
, 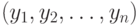 , где
, где  – количество тестированных.
– количество тестированных. - Для каждого задания группы
 выполняем предыдущий алгоритм.
выполняем предыдущий алгоритм. - Для каждого задания группы
 выполняем предыдущий алгоритм.
выполняем предыдущий алгоритм. - Находим коэффициент корреляции
 и
и  по формуле:
по формуле: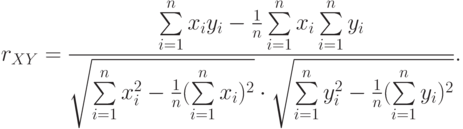
- Находим надежность
 всего теста по формуле (Спирмена-Брауна):
всего теста по формуле (Спирмена-Брауна):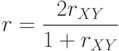
- Конец алгоритма.
Задача 5.
Необходимо на основе имеющихся результатов тестирования (матрица  ) получить для каждого из
) получить для каждого из  тестированных интегральный (обобщенный) показатель выполнения теста длины
тестированных интегральный (обобщенный) показатель выполнения теста длины  , а затем по вычисленным значениям этого интегрального показателя разбить всех тестированных на заданное количество
, а затем по вычисленным значениям этого интегрального показателя разбить всех тестированных на заданное количество  групп (задача классификации).
групп (задача классификации).
Алгоритм решения этой задачи состоит из следующих этапов.
- Если для
 -го задания увеличение значений результатов измерения свидетельствует об улучшении соответствующего свойства, то с ним свяжем признак
-го задания увеличение значений результатов измерения свидетельствует об улучшении соответствующего свойства, то с ним свяжем признак 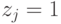 , а если свидетельствует об ухудшении – признак
, а если свидетельствует об ухудшении – признак 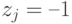 .
. - Выполняем нормирование элементов исходной матрицы так, чтобы в каждом столбце они изменялись в "одном направлении": для каждого задания (при фиксированном
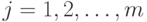 ) и для каждого испытуемого
) и для каждого испытуемого 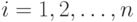 вычислим новое значение
вычислим новое значение
где
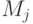 ,
, 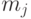 – наибольшее и наименьшее значения элементов
– наибольшее и наименьшее значения элементов  -го столбца и применяем преобразование вида
-го столбца и применяем преобразование вида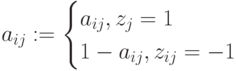 .
. - Для каждого столбца полученной новой матрицы
 (нормированной) вычисляется среднее квадратичное отклонение по формуле
(нормированной) вычисляется среднее квадратичное отклонение по формуле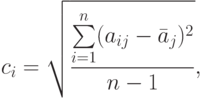
где
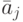 – среднее арифметическое элементов
– среднее арифметическое элементов  -го столбца.
-го столбца. - Вычисляется классификационный интегральный показатель
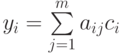 ,
,где
 – значение интегрального показателя для
– значение интегрального показателя для  -го обучаемого
-го обучаемого 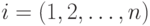 , – весовой коэффициент
, – весовой коэффициент  -го задания в тесте или в банке всех заданий,
-го задания в тесте или в банке всех заданий,  – элемент матрицы
– элемент матрицы  или его преобразованное (нормированное, например, по отношению к максимальному элементу или к норме матрицы).
или его преобразованное (нормированное, например, по отношению к максимальному элементу или к норме матрицы). - Находим наименьшее
 и наибольшее
и наибольшее  значения интегрального показателя (по всем тестированным). Отрезок
значения интегрального показателя (по всем тестированным). Отрезок ![[y_{max};y_{min}]](/sites/default/files/tex_cache/8149756d6ef62cb557156c581ca4756d.png) делим на заданное число
делим на заданное число  интервалов. Часто берут (при построении, например, гистограммы)
интервалов. Часто берут (при построении, например, гистограммы) 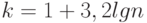 . Всех тестированных, для которых вычисленные значения интегрального показателя попадают в один и тот же интервал, отождествляем и относим к одному классу.
. Всех тестированных, для которых вычисленные значения интегрального показателя попадают в один и тот же интервал, отождествляем и относим к одному классу. - Выдаем результаты: значения интегрального показателя для каждого тестированного, а также его класс (или классификацию тестированных по интегральному показателю).
- Конец алгоритма.
Задача 6.
Дана интегральная норма  тестовых результатов. Необходимо разбить группу тестированных на несколько групп по их интегральным показателям (по отношению их к норме).
тестовых результатов. Необходимо разбить группу тестированных на несколько групп по их интегральным показателям (по отношению их к норме).
Приведем простейший алгоритм решения этой задачи.
Первый алгоритм решения этой задачи состоит из следующих этапов.
- Ввод входных данных:
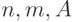 .
. - Для каждого тестированного определяем суммарный балл:
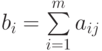 .
. - Разбиваем всю выборку тестированных на три группы: группа 1 с высокими баллами (нижняя граница суммарного балла для попадающих в эту группу равна
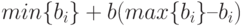 , группа 2 со средними баллами и группа 3 с низкими баллами (верхняя граница суммарного балла для попадающих в эту группу равна
, группа 2 со средними баллами и группа 3 с низкими баллами (верхняя граница суммарного балла для попадающих в эту группу равна 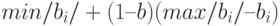 , где
, где  – масштабирующий коэффициент,
– масштабирующий коэффициент, 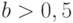 .
. - Конец алгоритма.
Задача 7.
Необходимо отсеять первичные ("сырые") результаты в группах, т.е. по данным 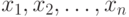 (процент выполнения, валидность и т.д.) выяснить задания (тесты, результаты), которые не согласуются с общей картиной тестирования.
(процент выполнения, валидность и т.д.) выяснить задания (тесты, результаты), которые не согласуются с общей картиной тестирования.
Алгоритм решения задачи состоит из следующих этапов.
- Вычисляется средняя величина
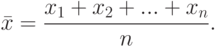
- Вычисляются наибольшее
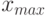 и наименьшее
и наименьшее 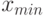 в группе.
в группе. - Вычисляются наибольшее отклонение в группе:

- Вычисляется относительное отклонение:
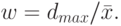
- Находим по таблице распределения Стьюдента процентные точки для
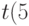 и
и  . Таблица Стьюдента имеется практически во всех справочниках по математической статистике.
. Таблица Стьюдента имеется практически во всех справочниках по математической статистике. - Вычисляем соответствующие точки
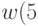 ,
, 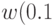 .
. - Если
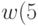 , то отсеиваем рассматриваемое данное и пересчитываем все заново (повторяем заново пункты 1-6).
, то отсеиваем рассматриваемое данное и пересчитываем все заново (повторяем заново пункты 1-6). - Конец алгоритма.
