|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
Как сказано выше, множество многочленов 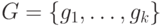 и
алгоритм нормальной формы
позволяют сформировать
множества
и
алгоритм нормальной формы
позволяют сформировать
множества  , каждое из которых получается путем умножения
многочлена
, каждое из которых получается путем умножения
многочлена  на некоторое множество мономов.
на некоторое множество мономов.  -полиномы
соответствуют многочленам
-полиномы
соответствуют многочленам  и мономам
и мономам  , таким,
что
, таким,
что  является минимальным (относительно деления мономов)
мономом, для
которого
является минимальным (относительно деления мономов)
мономом, для
которого  . В действительности, проверять
редуцируемость к нулю нужно только для таких многочленов
(заметим, что при этом рассматриваются не все
. В действительности, проверять
редуцируемость к нулю нужно только для таких многочленов
(заметим, что при этом рассматриваются не все  -полиномы,
автоматически используется "правило треугольника").
Естественно потребовать, чтобы множество
-полиномы,
автоматически используется "правило треугольника").
Естественно потребовать, чтобы множество  было
авторедуцированным.
было
авторедуцированным.
Алгоритм пополнения основан на описанном выше методе  -полиномов и отличается от приведенного выше алгоритма тем,
что в случае
нередуцируемости
-полиномов и отличается от приведенного выше алгоритма тем,
что в случае
нередуцируемости  -полинома его нормальная форма добавляется к
множеству
-полинома его нормальная форма добавляется к
множеству  . При этом, как правило, меняется алгоритм
нормальной формы, т.е. множества
. При этом, как правило, меняется алгоритм
нормальной формы, т.е. множества  , описанные выше.
, описанные выше.
Как правило, для повышения эффективности алгоритмов построения базисов
Гребнера совершенствуются методы перебора  -полиномов, но
мало внимания уделяется рассмотрению возможных алгоритмов нормальной формы.
-полиномов, но
мало внимания уделяется рассмотрению возможных алгоритмов нормальной формы.
До настоящего момента мы никак не ограничивали выбор алгоритма нормальной
формы, т.е. формирование множеств  для заданной
системы многочленов
для заданной
системы многочленов 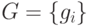 . Теперь предположим, что на
множестве мономов задано некоторое отношение "делимости"
. Теперь предположим, что на
множестве мономов задано некоторое отношение "делимости"  ,
удовлетворяющее следующим аксиомам (аксиомы глобального
инволютивного деления,
см., например,
[
22
]
:
,
удовлетворяющее следующим аксиомам (аксиомы глобального
инволютивного деления,
см., например,
[
22
]
:
-
 (в смысле обычного
деления);
(в смысле обычного
деления); -
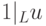 ;
; -
 ;
; -
 ;
; -
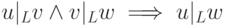 (транзитивность).
(транзитивность).
В случае, если имеет место отношение 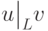 , мы будем
говорить, что
, мы будем
говорить, что  инволютивно делит
инволютивно делит  .
.
Аксиомы 3 и 4 для случая двух переменных можно наглядно представить следующим образом.
Изобразим мономы вида  на плоскости точками с
координатами
на плоскости точками с
координатами  . Тогда
. Тогда
- множества инволютивных кратных для любых двух мономов либо не пересекаются, либо одно из них содержится в другом;
- множество кратных монома
 представляется либо одной
точкой
представляется либо одной
точкой  , либо вертикальным или горизонтальным лучом,
выходящим из этой точки, либо углом между вертикальным и горизонтальным
лучами, выходящими из этой точки.
, либо вертикальным или горизонтальным лучом,
выходящим из этой точки, либо углом между вертикальным и горизонтальным
лучами, выходящими из этой точки.
Обобщение на случай нескольких переменных очевидно.
10.2. УПРАЖНЕНИЕ.
Показать, что глобальное инволютивное деление определяет для каждого монома  множество
множество 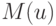 его мультипликативных
переменных как множество таких
переменных, что
его мультипликативных
переменных как множество таких
переменных, что  инволютивно делит любое произведение
инволютивно делит любое произведение  на моном, включающий только мультипликативные переменные. Остальные переменные
назовем немультипликативными для монома
на моном, включающий только мультипликативные переменные. Остальные переменные
назовем немультипликативными для монома  (обозначение
(обозначение 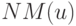 ).
).
Примеры глобальных инволютивных делений:
-
 - правое деление Поммаре.
- правое деление Поммаре. -
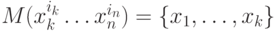 - левое деление
Поммаре.
- левое деление
Поммаре. -
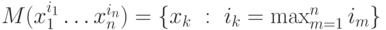 .
.
Для двух переменных правое и левое деление Поммаре можно проиллюстрировать следующим образом:


Для третьего примера геометрическая интерпретация выглядит следующим образом:

10.4. УПРАЖНЕНИЕ.
В кольце многочленов ![K[x,y,z]](/sites/default/files/tex_cache/6615709b54bf0d76ba4400c16b6273b5.png) найти мультипликативные и
немультипликативные переменные для мономов
найти мультипликативные и
немультипликативные переменные для мономов  ,
,  ,
, 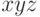 для каждого из глобальных инволютивных делений, рассмотренных в примерах 10.3.
для каждого из глобальных инволютивных делений, рассмотренных в примерах 10.3.
Можно рассмотреть более общую ситуацию, когда фиксировано некоторое
конечное множество  мономов, а инволютивное деление
зависит от этого множества. При этом в левой части отношения
мономов, а инволютивное деление
зависит от этого множества. При этом в левой части отношения 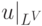 могут стоять только мономы из множества
могут стоять только мономы из множества  .
.
10.5. ОПРЕДЕЛЕНИЕ.
Согласно
[
21
]
,
на моноиде  задано инволютивное деление
задано инволютивное деление  , если для
каждого конечного подмножества
, если для
каждого конечного подмножества 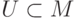 и для каждого монома
и для каждого монома 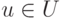 определен подмоноид
определен подмоноид 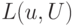 моноида
моноида  , удовлетворяющий следующим
условиям:
, удовлетворяющий следующим
условиям:
- Если
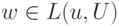 и
и 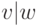 , то
, то  ;
; - Если
 и
и 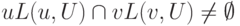 ,
то
,
то 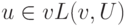 или
или  ;
; - Если
 и
и  , то
, то  ;
; - Если
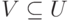 , то
, то 
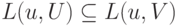 .
.
Образующие моноида 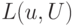 называются мультипликативными переменными для
называются мультипликативными переменными для  . Если
. Если 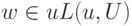 , то пишут
, то пишут 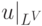 , и моном
, и моном  называется (
называется (  )- инволютивным делителем монома
)- инволютивным делителем монома  а моном
а моном  называется (
называется (  )- инволютивным кратным
монома
)- инволютивным кратным
монома  . В этом случае
равенство
. В этом случае
равенство  мы будем записывать в виде
мы будем записывать в виде  , в противном случае - в виде
, в противном случае - в виде 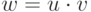 , и моном
, и моном  будем
называть немультипликативным
для
будем
называть немультипликативным
для  .
.
10.6. УПРАЖНЕНИЕ. Показать, что глобальное инволютивное деление является инволютивным делением в смысле определения 10.5.
