|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
9.33. ТЕОРЕМА.
Пусть  - свободный
- свободный  -модуль,
-модуль, 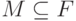 - его
- его  -подмодуль,
-подмодуль,  - конечное множество, -
ранжир на множестве
термов
- конечное множество, -
ранжир на множестве
термов 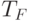 . Предположим, что множество
. Предположим, что множество  нормализовано таким
образом, что
нормализовано таким
образом, что  для всех
для всех  .
Тогда эквивалентны
следующие условия:
.
Тогда эквивалентны
следующие условия:
(1)  является
является  -базисом модуля
-базисом модуля  ;
;
(1') любой элемент модуля  допускает нормальное
допускает нормальное  -представление;
-представление;
(2)  порождает
порождает  ;
;
(4) если  и
и  нередуцируемы, то
нередуцируемы, то  ;
;
(5) если  и
и  нередуцируем, то
нередуцируем, то  .
.
Следующие условия являются необходимыми для выполнения
предыдущих, и, если множество  порождает
порождает  , то они
являются и
достаточными:
, то они
являются и
достаточными:
(6) если  и
и  , то
, то  допускает
допускает  -представление;
-представление;
(6') если 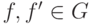 и
и  , то
, то  допускает нормальное
допускает нормальное  -представление;
-представление;
(7) если  и
и  определен, то в
определен, то в  существуют элементы
существуют элементы  , такие,
что
, такие,
что

 -элемент
-элемент  ,
, 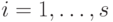 , допускает
, допускает  -представление;
-представление;(7') если  и
и  определен,
то в
определен,
то в  существуют элементы
существуют элементы  , удовлетворяющие условию (9.7), такие, что каждый
, удовлетворяющие условию (9.7), такие, что каждый  -элемент
-элемент  ,
, 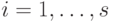 , допускает нормальное
, допускает нормальное  -представление;
-представление;
(8) если 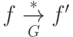 ,
,  и
и 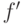 и
и 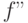 нередуцируемы, то
нередуцируемы, то  ;
;
(9) если 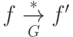 ,
,  , то существует элемент
, то существует элемент  ,
такой, что
,
такой, что 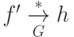 ,
,  , т.е.
, т.е.  удовлетворяет
условию слияния;
удовлетворяет
условию слияния;
(10) 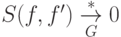 для любых
для любых  ;
;
(10')  для любых
для любых  ;
;
(11) если 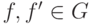 и
и  определен,
то в
определен,
то в  существуют элементы
существуют элементы 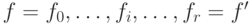 ,
удовлетворяющие условию (9.7) и такие, что
,
удовлетворяющие условию (9.7) и такие, что  для всех
для всех  ;
;
(11') если 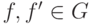 и
и  определен, то
в
определен, то
в  существуют элементы
существуют элементы 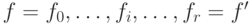 ,
удовлетворяющие условию и такие, что
,
удовлетворяющие условию и такие, что 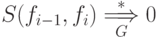 для всех
для всех  .
.
ДОКАЗАТЕЛЬСТВО. Докажем следующие импликации:

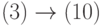 . Тривиально, поскольку
. Тривиально, поскольку  .
.
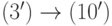 . Аналогично.
. Аналогично.
 . Достаточно положить
. Достаточно положить 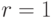 .
.
 . Аналогично.
. Аналогично.
 . Тривиально.
. Тривиально.
 . По предложению (9.23) множество нередуцируемых элементов
является векторным пространством, значит, если
. По предложению (9.23) множество нередуцируемых элементов
является векторным пространством, значит, если  и
и 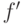 нередуцируемы, то и их разность нередуцируема. Поскольку
нередуцируемы, то и их разность нередуцируема. Поскольку  , из
3 и предыдущего замечания следует, что
, из
3 и предыдущего замечания следует, что 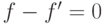 , т.е. (4)
, т.е. (4)
 . Полагаем
. Полагаем  .
.
 . Достаточно применить леммы 9.21 и
9.22.
. Достаточно применить леммы 9.21 и
9.22.
 . Очевидно.
. Очевидно.
 . Пусть
. Пусть  и
и  . Тогда элемент
. Тогда элемент  не может редуцироваться к 0,
что противоречит (3).
не может редуцироваться к 0,
что противоречит (3).
 . Пусть существуют
. Пусть существуют 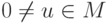 , для
которых нет нормального
, для
которых нет нормального  -представления. Среди таких элементов
выберем
элемент с минимальным
-представления. Среди таких элементов
выберем
элемент с минимальным  . По условию (2) можно применить шаг редукции, сокращающий
. По условию (2) можно применить шаг редукции, сокращающий  . Полученное
противоречие с минимальностью
. Полученное
противоречие с минимальностью  доказывает (1')).
доказывает (1')).
 . Очевидно.
. Очевидно.
 . Достаточно заметить, что если
. Достаточно заметить, что если  ,
,  , то
, то 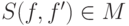 .
.
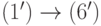 . Аналогично.
. Аналогично.
 . Очевидно.
. Очевидно.
 . Также очевидно.
. Также очевидно.
 . Очевидно.
. Очевидно.
 . Пусть
. Пусть 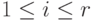 ,
,  и
и  ,
,  ,
,  ,
,  ,
,  -
-  -представление элемента
-представление элемента  . Положим
. Положим  . Тогда
. Тогда
![u=u_1 \xrightarrow[G]{} u_2 \xrightarrow[G]{}\dots \xrightarrow[G]{} u_r
\xrightarrow[G]{}0.](/sites/default/files/tex_cache/ff4e1e4e1c5cc438e922938aab006b19.png)
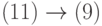 . Ввиду леммы 9.32, достаточно доказать, что отношение
редукции удовлетворяет псевдолокальному условию слияния. Пусть
. Ввиду леммы 9.32, достаточно доказать, что отношение
редукции удовлетворяет псевдолокальному условию слияния. Пусть  ,
,  . Это означает существование
элементов
. Это означает существование
элементов 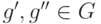 ,
,  ,
,  ,
,  , таких, что
, таких, что  ,
,  , где
, где  ,
,  , но
, но  . Можно предполагать, что
. Можно предполагать, что  . Обозначим
. Обозначим 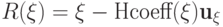 для любого
для любого 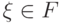 .
.
Выделим в  слагаемое
слагаемое  , т.е.
, т.е.  , где
, где 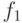 состоит из слагаемых,
которые больше, чем
состоит из слагаемых,
которые больше, чем  , а
, а  - из слагаемых, меньших
- из слагаемых, меньших  . Нужно рассмотреть два случая:
. Нужно рассмотреть два случая:  и
и  . В первом из них, полагая
. В первом из них, полагая  и
и  , по
лемме 9.28 получаем
, по
лемме 9.28 получаем 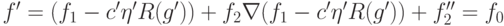 , откуда
, откуда  .
.
В случае, когда 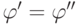 , одновременно выполняются
условия
, одновременно выполняются
условия  и
и  . Поэтому
определен
. Поэтому
определен  . По условию 11 доказываемой теоремы в
. По условию 11 доказываемой теоремы в  существует последовательность
существует последовательность  , удовлетворяющая условию (9.7) и
такая, что
, удовлетворяющая условию (9.7) и
такая, что  для любого
для любого  .
Значит,
.
Значит,  для любого
для любого  , поэтому
существуют
, поэтому
существуют  , такие, что
, такие, что  ,
,  и
и  ,
,  . Покажем, что
. Покажем, что  . Это
следует из того, что
. Это
следует из того, что

 и удовлетворяет условию
и удовлетворяет условию  . Следовательно, отношение
. Следовательно, отношение  удовлетворяет псевдолокальному условию слияния.
удовлетворяет псевдолокальному условию слияния. . Если множество
. Если множество  порождает
порождает  , то по лемме 9.24
существуют элементы
, то по лемме 9.24
существуют элементы  ,
такие, что для любого
,
такие, что для любого  либо
либо  , либо
, либо 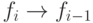 . Пусть
. Пусть  обозначает наибольший
индекс, для которого не
выполняется условие
обозначает наибольший
индекс, для которого не
выполняется условие  . Тогда
. Тогда  и
и  . По
условию 9
. По
условию 9  , и получаем противоречие с выбором
, и получаем противоречие с выбором  , поскольку
, поскольку  редуцируется только в самого себя.
редуцируется только в самого себя.
 .
.  ,
следовательно,
,
следовательно,  .
.
 . Пусть
. Пусть  и
и 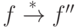 . Выберем нередуцируемые
. Выберем нередуцируемые 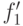 и
и  такие, что
такие, что  ,
,  . Из (8) следует, что
. Из (8) следует, что  , т.е. отношение
, т.е. отношение  удовлетворяет условию слияния.
удовлетворяет условию слияния.
Поскольку вопрос о  -представимости элемента может быть решен
алгоритмически, пункт (6')
дает нам возможность сформулировать алгоритм проверки, является ли данная
система образующих
подмoдуля его базисом Гребнера. Пункт (7')
этой же теоремы позволяет нам оптимизировать полученный алгоритм,
проверяя
-представимости элемента может быть решен
алгоритмически, пункт (6')
дает нам возможность сформулировать алгоритм проверки, является ли данная
система образующих
подмoдуля его базисом Гребнера. Пункт (7')
этой же теоремы позволяет нам оптимизировать полученный алгоритм,
проверяя  -представимость не всего множества
-представимость не всего множества  -элементов,
а только некоторого его подмножества.
-элементов,
а только некоторого его подмножества.

 ;
; ;
;