|
Упражнение 2.1.25 |
Основные свойства контекстно-свободных языков
9.7*. Теорема Парика
Замечание 9.1.7.
В этом разделе предполагается, что зафиксирован некоторый линейный
порядок на алфавите  .
Пусть
.
Пусть 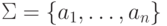 .
.
Определение 9.7.2.
Через 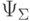 будем обозначать функцию
из
будем обозначать функцию
из 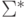 в
в 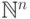 ,
определенную следующим образом:
,
определенную следующим образом: 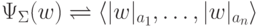 .
Аналогично, каждому языку
.
Аналогично, каждому языку  ставится в соответствие множество
ставится в соответствие множество 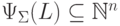 ,
определенное следующим образом:
,
определенное следующим образом:
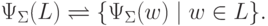
Пример 9.7.3.
Пусть 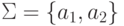 и L = {a1,a1a2a2,a2a2a1}.
Тогда
и L = {a1,a1a2a2,a2a2a1}.
Тогда 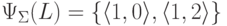 .
.
Определение 9.7.4.
Пусть 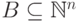 и
и 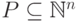 .
Тогда через
.
Тогда через 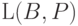 обозначается множество
обозначается множество
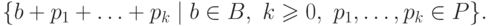
Определение 9.7.5.
Множество 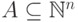 называется линейным
(linear),
если A = L(B,P)
для некоторых конечных множеств B и P.
называется линейным
(linear),
если A = L(B,P)
для некоторых конечных множеств B и P.
Определение 9.7.6.
Множество 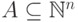 называется полулинейным
(semilinear), если
оно является объединением конечного числа линейных множеств.
называется полулинейным
(semilinear), если
оно является объединением конечного числа линейных множеств.
Теорема 9.7.7 (Теорема Парика). Если язык  является контекстно-свободным,
то множество
является контекстно-свободным,
то множество 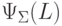 является полулинейным.
является полулинейным.
Доказательство можно найти в [Гин, с. 207-211].
Пример 9.7.8.
Пусть  .
Рассмотрим язык
.
Рассмотрим язык 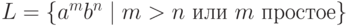 .
Можно проверить, что множество
.
Можно проверить, что множество 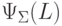 не является полулинейным.
Следовательно, язык L
не является контекстно-свободным.
не является полулинейным.
Следовательно, язык L
не является контекстно-свободным.
Теорема 9.7.9. Если множество 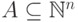 является полулинейным,
то существует такой автоматный язык L, что
является полулинейным,
то существует такой автоматный язык L, что 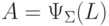 .
.
Доказательство.
Докажем это для произвольного линейного множества A = L(B,P)
(на полулинейные множества утверждение распространяется
по теореме 3.1.1).
Рассмотрим конечный автомат 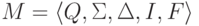 ,
где Q = {1,2}, I = {1}, F = {2}
и
,
где Q = {1,2}, I = {1}, F = {2}
и
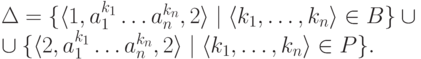
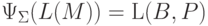 .
.Замечание 9.7.10. Теорема 9.3.1 является следствием теорем 9.7.7 и 9.7.9.


