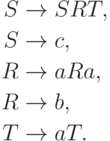|
Упражнение 2.1.25 |
Нормальные формы контекстно-свободных грамматик
Основная цель этой лекции - доказать, что каждая контекстно-свободная грамматика эквивалентна некоторой контекстно-свободной грамматике специального вида, а именно грамматике в нормальной форме Хомского (раздел 8.3). Этот факт используется дальше в доказательствах многих теорем о контекстно-свободных языках. Два вспомогательных результата, на которые опирается приведение грамматик к нормальной форме Хомского, выделены в отдельные разделы в начале лекции.
В конце лекции доказывается, что каждую контекстно-свободную грамматику можно также привести к нормальной форме Грейбах.
8.1. Устранение бесполезных символов
Определение 8.1.1.
Пусть дана порождающая грамматика 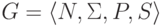 .
Символ
.
Символ 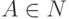 называется полезным
(useful), если
существуют такие слова
называется полезным
(useful), если
существуют такие слова  ,
, 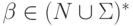 и
и 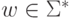 ,
что
,
что 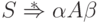 и
и 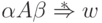 .
Символ
.
Символ 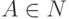 называется бесполезным
(useless),
если он не является полезным.
Символ
называется бесполезным
(useless),
если он не является полезным.
Символ 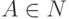 называется порождающим
(generating),
если
существует такое слово
называется порождающим
(generating),
если
существует такое слово 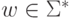 ,
что
,
что  .
Символ
.
Символ 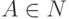 называется достижимым
если существуют такие слова
называется достижимым
если существуют такие слова  и
и 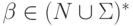 ,
что
,
что 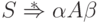 .
.
Лемма 8.1.2. Пусть дана
контекстно-свободная грамматика 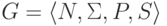 , в которой все символы из N являются порождающими.
Пусть N' - множество всех достижимых символов грамматики G, а P' - множество тех правил из P, которые не содержат ни одного символа из множества
, в которой все символы из N являются порождающими.
Пусть N' - множество всех достижимых символов грамматики G, а P' - множество тех правил из P, которые не содержат ни одного символа из множества  . Тогда
в контекстно-свободной грамматике
. Тогда
в контекстно-свободной грамматике 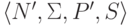 все символы из N' являются порождающими.
\end{lemma}
все символы из N' являются порождающими.
\end{lemma}
Теорема 8.1.3. Пусть дана
контекстно-свободная грамматика 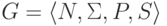 и
и  . Тогда существуют такие множества
. Тогда существуют такие множества 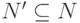 и
и 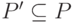 , что
в контекстно-свободной грамматике
, что
в контекстно-свободной грамматике 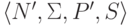 нет бесполезных символов
и она эквивалентна исходной грамматике.
нет бесполезных символов
и она эквивалентна исходной грамматике.
Доказательство. На первом этапе удалим все непорождающие символы (удалим также каждое правило, содержащее хотя бы один такой символ). На втором этапе из полученной грамматики удалим все недостижимые символы (и правила, их содержащие). Согласно 8.1.2 на втором этапе ни один порождающий символ не может стать непорождающим.
Пример 8.1.4. Рассмотрим контекстно-свободную грамматику G с правилами
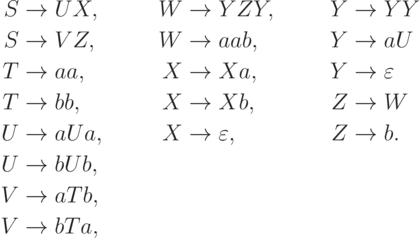
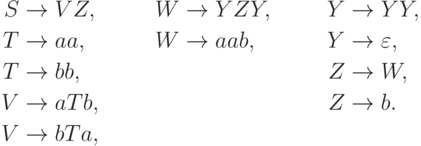
Упражнение 8.1.5. Найти контекстно-свободную грамматику без бесполезных символов, эквивалентную грамматике