НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 7: Синтаксические моноиды

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: свободно | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать программу

6.4*. Классы эквивалентности слов

Лемма 6.4.1. Пусть $L \subseteq \Sigma ^*$ и $y \in \Sigma ^*$ . Тогда

$\begin{align*} \rightcontext_{\Sigma ^* \sminus L} ( y ) &= \Sigma ^* \sminus \rightcontext_{L} ( y ) ,\\ \bothcontext_{\Sigma ^* \sminus L} ( y ) &= (\Sigma ^* \times \Sigma ^*) \sminus \bothcontext_{L} ( y ) . \end{align*}$

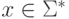Определение 6.4.2. Пусть $L \subseteq \Sigma ^*$ и $x \in \Sigma ^*$ . Обозначим через $[ x ]\supright_{L}$ язык $\{ y \in \Sigma ^* \mid \rightcontext_{L} ( y ) = \rightcontext_{L} ( x ) \}$ . Обозначим через $[ x ]_{L}$ язык $\{ y \in \Sigma ^* \mid \bothcontext_{L} ( y ) = \bothcontext_{L} ( x ) \}$ .

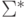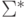Пример 6.4.3. Пусть $L \subseteq \Sigma ^*$ . Множества вида $[ x ]\supright_{L}$ образуют разбиение множества $\Sigma ^*$ на классы эквивалентности. Множества вида $[ x ]_{L}$ образуют разбиение множества $\Sigma ^*$ на классы эквивалентности.

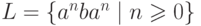Пример 6.4.4. Пусть $\Sigma = \{ a , b \}$ и $L = \{ a^n b a^n \mid n \geq 0 \}$ . Тогда

$\begin{align*} [baa]\supright_{L} &= \{ a^i b a^j \mid 0 \leq i < j \} \cup \{ y \in \Sigma ^* \mid | y |_b > 1 \} ,\\ [baa]_{L} &= \{ a^i b a^{i+2} \mid i \geq 0 \} . \end{align*}$

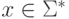Лемма 6.4.5. Если язык $L \subseteq \Sigma ^*$ является автоматным, то для каждого слова $x \in \Sigma ^*$ языки $[ x ]\supright_{L}$ и $[ x ]_{L}$ являются автоматными.

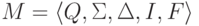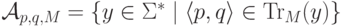Доказательство. Пусть язык L распознается конечным автоматом $M = \lalg Q , \Sigma , \Delta , I , F \ralg$ , не содержащим переходов с метками длины больше единицы. Будем использовать обозначение Tr_M из доказательства теоремы 6.3.11. При любой фиксированной паре $\lp p , q \rp \in Q \times Q$ язык $\cala _{ p , q , M } = \{ y \in \Sigma ^* \mid \lp p , q \rp \in \mathrm{Tr}_M( y ) \}$ является автоматным (он распознается конечным автоматом $\lalg Q , \Sigma , \Delta , \{ p \} , \{ q \} \ralg$ ). 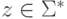Для каждого слова $z \in \Sigma ^*$ язык $\calb _{ z , M } = \{ y \in \Sigma ^* \mid \mathrm{Tr}_M( y ) = \mathrm{Tr}_M( z ) \}$ является автоматным, так как он представим в виде пересечения конечного семейства автоматных языков:

$\calb _{ z , M } = \biggl(\, \raisebox{0pt}[\height][0.95\depth]{\displaystyle \bigcap _{ \lp p , q \rp \in \mathrm{Tr}_M( z ) }} \cala _{ p , q , M } \biggr) \cap \biggl(\, \raisebox{0pt}[\height][0.95\depth]{\displaystyle \bigcap _{ \lp p , q \rp \notin \mathrm{Tr}_M( z ) }} ( \Sigma ^* \sminus \cala _{ p , q , M } )\biggr) .$

Каждый из языков [x]_L и $[ x ]\supright_{L}$ является объединением конечного семейства автоматных языков:

$\raisebox{0pt}[\height][0pt]{\displaystyle [ x ]_{L} = \bigcup _{ z \in [ x ]_{L} } \calb _{ z , M }} , \qquad \raisebox{0pt}[\height][0pt]{\displaystyle [ x ]\supright_{L} = \bigcup _{ z \in [ x ]\supright_{L} } \calb _{ z , M }} .$

Замечание 6.4.6. Из теоремы 6.1.8 вытекает, что если язык L автоматный, то существует лишь конечное число различных множеств $[ x ]\supright_{L}$ . Аналогичное утверждение верно для множеств $[ x ]_{L}$ (см. теорему 6.3.11).

Пример 6.4.7. Рассмотрим язык

$L = \{ (ab)^n \mid n \geq 0 \} \cup \{ (ab)^n a \mid n \geq 0 \}$

над алфавитом $\Sigma = \{ a , b \}$ . Тогда

$\begin{align*} [ \varepsilon ]\supright_{L} &= (ab)^* ;\\ [ a ]\supright_{L} &= (ab)^* a ;\\ [ b ]\supright_{L} &= b (a \replus b)^* \replus (a \replus b)^* (aa \replus bb) (a \replus b)^* ;\\ [ \varepsilon ]_{L} &= 1 ;\\ [ ab ]_{L} &= (ab)^+ ;\\ [ ba ]_{L} &= (ba)^+ ;\\ [ a ]_{L} &= (ab)^* a ;\\ [ b ]_{L} &= b (ab)^* ;\\ [ aa ]_{L} &= (a \replus b)^* (aa \replus bb) (a \replus b)^* . \end{align*}$

Упражнение 6.4.8. Существуют ли такие языки $L_1 \subseteq \Sigma ^*$ и $L_2 \subseteq \Sigma ^*$ , что язык L₁ является автоматным, но язык

$L_3 = \{ x \in \Sigma ^* \mid x y \in L_1 \mathspace\text{для некоторого слова}\mathspace y \in L_2 \}$

не является автоматным?

Упражнение 6.4.9. Существуют ли такие языки $L_1 \subseteq \Sigma ^*$ и $L_2 \subseteq \Sigma ^*$ , что язык L₁ является автоматным, но язык

$L_3 = \{ x \in \Sigma ^* \mid x y \in L_1 \mathspace\text{для всех слов}\mathspace y \in L_2 \}$

не является автоматным?

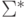Упражнение 6.4.10. Существует ли такой автоматный язык $L \subseteq \Sigma ^*$ , что язык

$\mathrm{Max} ( L ) \bydef \{ x \in L \mid x y \notin L \mathspace\text{для всех слов}\mathspace y \in \Sigma ^+ \}$

не является автоматным?

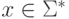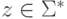Теорема 6.4.11. Язык $L \subseteq \Sigma ^*$ является автоматным тогда и только тогда, когда существует такое отношение эквивалентности $R \subseteq \Sigma ^* \times \Sigma ^*$ , что R разбивает $\Sigma ^*$ на конечное множество классов эквивалентности, L является объединением некоторых из этих классов эквивалентности и для любых $x \in \Sigma ^*$ , $y \in \Sigma ^*$ , $z \in \Sigma ^*$ из xRy следует xzRyz.

Замечание 6.4.12. Теоремы 6.1.8 и 6.4.11 образуют теорему Майхилла-Нерода.

Дальше >>

Математическая теория формальных языков

Математическая теория формальных языков

Синтаксические моноиды

6.4*. Классы эквивалентности слов

Вопросы и ответы

Студенты

Авторизоваться

Математическая теория формальных языков

Математическая теория формальных языков

Синтаксические моноиды

6.4*. Классы эквивалентности слов

Вопросы и ответы

Студенты