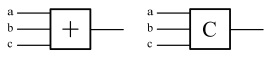| Россия, Сургут |
Азы (nuts and bolts) классических вычислении
Если теперь построить дизъюнкцию трех сформированных конъюнкций, то получим:
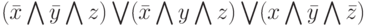
Это выражение называется совершенной дизъюнктивной нормальной формой (ДНФ) функции f . ДНФ генерирует для всех наборов х, у, z такие же значения, которые представлены в таблице истинности функции f . Ясно, что этот подход работает для любой булевой функции. Мы получили следующую
Теорема. Любая булева функция 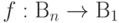 может быть выражена через элементарные функции {АND, OR, NOT} в виде ДНФ.
может быть выражена через элементарные функции {АND, OR, NOT} в виде ДНФ.
При проектировании логической схемы следует минимизировать число логических элементов, что позволяет уменьшить стоимость, затраты энергии, увеличить быстродействие. ДНФ, способные реализовать любую булеву функцию, обычно не дают оптимального решения. Проиллюстрируем это на следующем примере.
Рассмотрим функцию f , которая реализует сложение двух 2-битных целых: 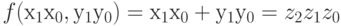 . Эта функция принимает 4 бита на входе (мы отделяем запятой два бита только для удобства чтения) и возвращает 3 бита на выходе. Поскольку сумма двух 2-битных значений может давать 3-битный результат, то на выходе всегда возвращаются 3 бита. Например, 3+2 = 5, что в бинарном представлении имеет вид: 11+10 = 101, f (1110) = 101.
. Эта функция принимает 4 бита на входе (мы отделяем запятой два бита только для удобства чтения) и возвращает 3 бита на выходе. Поскольку сумма двух 2-битных значений может давать 3-битный результат, то на выходе всегда возвращаются 3 бита. Например, 3+2 = 5, что в бинарном представлении имеет вид: 11+10 = 101, f (1110) = 101.
Используя сложение целых в бинарной форме, функцию f можно задать следующей таблицей:
Мы можем функцию f рассматривать как три функции, каждая из которых вычисляет один бит результата: 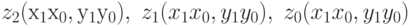 .
.
Давайте оценим сложность ДНФ для этих трех функций. В качестве меры сложности примем сумму конъюнкций и дизъюнкций в ДНФ. Для простоты будем пренебрегать числом отрицаний в ДНФ (эта операция менее дорогая в реализации).
Для функций 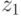 и
и 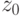 значение 1 встречается в 8 строках таблицы, для функции
значение 1 встречается в 8 строках таблицы, для функции 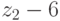 раз. Следовательно, сложность ДНФ для функций
раз. Следовательно, сложность ДНФ для функций 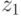 и
и 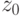 равна 8 х 3+ 7 = 31, а для функции
равна 8 х 3+ 7 = 31, а для функции  .
.
Сложность ДНФ неоправданно велика, поскольку не учитывает никакую внутреннюю логику, свойственную функции.
Например, 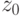 вычисляет сумму последних битов, которая определяет ее четность, зависящую от четности аргументов суммы. Сумма двух четных - четна, четного и нечетного - нечетна, двух нечетных - четна. Следовательно,
вычисляет сумму последних битов, которая определяет ее четность, зависящую от четности аргументов суммы. Сумма двух четных - четна, четного и нечетного - нечетна, двух нечетных - четна. Следовательно, 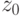 зависит только от
зависит только от 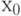 и
и 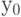 и может быть задана следующей формулой:
и может быть задана следующей формулой:
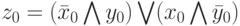
Сложность выражения в этой формуле равна 3, что значительно меньше 31- сложности ДНФ для 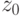 .
.
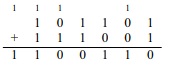
Когда нам нужно сложить два больших числа, то мы не пользуемся "таблицей сложения", как это было сделано в примере сложения 2-битных чисел, а пользуемся методом сложения "в столбик". Этот метод работает и для бинарных чисел, например, сложение 45 + 57 = 102 в бинарной форме имеет вид:
Переносы указаны в верхней строке.
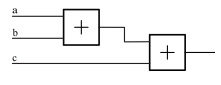
Представим выше приведенную булеву формулу для сложения двух битов по модулю 2 следующей схемой: Для упрощения диаграмм представим
данную схему как один стандартный элемент "+ ". Тогда булева функция: а + b + с mod 2 может быть реализована схемой:
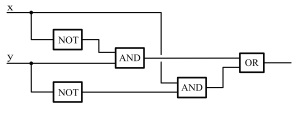
Еще одна операция, которая нам необходима для реализации длинного сложения "столбиком", - это вычисление переноса, который появляется, когда мы складываем 3 бита (два входных бита и бит переноса из предыдущего разряда). Заметьте, что при сложении а + b + с перенос появляется только тогда, когда по крайней мере два бита имеют значение 1, так что функция переноса может быть задана следующим выражением: 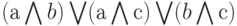 со сложностью 5. Функцию можно упростить и представить в виде:
со сложностью 5. Функцию можно упростить и представить в виде: 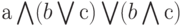 со сложностью 4. Схема для функции переноса имеет вид:
со сложностью 4. Схема для функции переноса имеет вид:
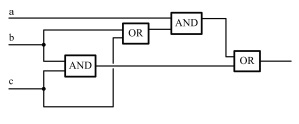
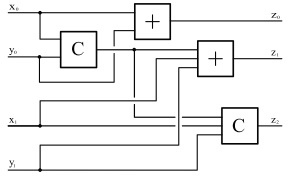
Теперь мы можем представить схему сложения двух 2-битных целых. Для упрощения диаграммы схемы для функции: а + b + с mod 2 и функции переноса будем рассматривать как стандартные элементы:
Заметьте, вычисление переноса для частного случая а + b дается формулой  .
.
В заключение приведем схему для вычисления 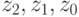 в
в  .
.
Вычисляя сложность данного стандартного элемента, можно видеть, что общая сложность этой схемы равна 1 + 3 + 6 + 4 = 14, что много лучше, чем 31 + 31 +23 = 85 - сложности, задаваемой ДНФ.