| Россия, Москва |
Способы представления ФАЛ. Переход от одной формы представления ФАЛ к другой
Основная форма представления функций алгебры логики – таблица истинности (ТИ), которая определяет значение функции на всех наборах переменных.
Таблицами истинности для функций одной и двух переменных являются таблицы 2.1 и 2.2 соответственно.
Помимо таблицы истинности, возможны и другие виды представления ФАЛ, наиболее распространенными из которых являются совершенная дизъюнктивная нормальная форма, описывающая все наборы переменных, на которых функция принимает значение, равное 1, и совершенная конъюнктивная нормальная форма, описывающая все наборы переменных, на которых функция принимает значение, равное 0.
Рассмотрим способы перехода от одного вида представления ФАЛ к другому.
Пример 2.1 Пусть ФАЛ задана в виде таблицы истинности (2.1).
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Получить СДНФ и СКНФ этой функции.
Решение
Получение СДНФ.
Для представления сокращенной записи СДНФ этой функции необходимо под знаком обобщенной дизъюнкции ? или V перечислить через запятую номера всех наборов, на которых функция принимает значение, равное 1.:
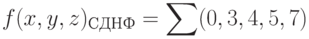
Получение развернутой записи СДНФ включает следующие этапы.
Этап 1.
Записать дизъюнкцию k конъюнктивных термов, содержащих все переменные, от которых зависит функция, где k – количество наборов, на которых функция принимает значение, равное единице, то есть количество наборов, перечисленное в сокращенной записи СДНФ:
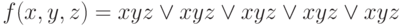
Этап 2.
Записать под каждым термом двоичный эквивалент одного из наборов, на которых функция принимает значение, равное единице:
Этап 3.
Расставить знаки отрицания над теми переменными, которым в двоичном эквиваленте соответствует 0:
Полученная запись представляет собой совершенную дизъюнктивную нормальную форму для функции, заданной таблицей истинности 2.1.
Получение СКНФ.
Для представления сокращенной записи СКНФ этой функции необходимо под знаком обобщенной конъюнкции ? или ? перечислить через запятую номера всех наборов, на которых функция принимает значение, равное 0:

Получение развернутой записи СДНФ включает следующие этапы.
Этап 1.
Записать конъюнкцию m дизъюнктивных термов, содержащих все переменные, от которых зависит функция, где m - количество наборов, на которых функция принимает значение, равное 0, то есть количество наборов, перечисленное в сокращенной записи СКНФ:
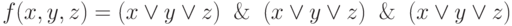
Этап 2.
Записать под каждым термом двоичный эквивалент одного из наборов, на которых функция принимает значение, равное 0:
Этап 3.
Расставить знаки отрицания над теми переменными, которым в двоичном эквиваленте соответствует 1:
Полученная запись представляет собой совершенную конъюнктивную нормальную форму для функции, заданной таблицей истинности 2.1.
Пример 2.2
Пусть ФАЛ задана сокращенной записью СДНФ:
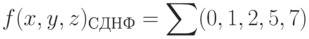
Представить таблицу истинности, а также полную и сокращенную записи СКНФ этой функции.
Решение
Получение таблицы истинности
Этап 1.
Подготовить ТИ для логической функции трех переменных
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | |
| 6 | 1 | 1 | 0 | |
| 7 | 1 | 1 | 1 |
Этап 2.
Записать 1 в качестве значения функции в строки, соответствующие наборам, перечисленным в сокращенной записи СДНФ.
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | |
| 7 | 1 | 1 | 1 | 1 |
Этап 3.
Записать 0 в качестве значения функции в остальные строки таблицы.
| Номер набора | x | y | z | f(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Таблица истинности получена.
Получение СКНФ.
Получение СКНФ по ТИ описано в примере 2.1.
Результатом будет: