НОУ ИНТУИТ | Теория экспериментов с конечными автоматами. Лекция 22: Разновидности экспериментов с билинейными автоматами

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 17.02.2011 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 3 студентам

| Поделиться |

Поддержать программу

Здесь матрицы со звездочкой имеют следующую блочную структуру:

$A*= \left [ \begin {matrix} A_0&A_1& \dots & A_h\\ E_n& 0_n & \dots &0_n\\ \dots & \dots & \dots & \dots \\ 0_n & \dots & E_n & 0_n \end {matrix} \right ]$

где в роли блоков выступают матрицы размерности $n \times n$ , а число блочных строк и столбцов равно h+1 ;

$F_i*= \left [ \begin {matrix} F_i^{(0)}& F_i^{(1)}& \dots & F_i^{(h)}\\ 0_n& 0_n& \dots & 0_n\\ \dots & \dots & \dots & \dots \\ 0_n& 0_n& \dots & 0_n \end {matrix} \right ]$

где в роли блоков выступают матрицы размерности $n \times n$ , а число блочных строк и столбцов равно h+1 ;

$B*= \left [ \begin {matrix} B\\ [0]\\ \dots \\ [0] \end {matrix} \right ]$

где в роли блоков выступают матрицы размерности $n \times l$ , а число блочных строк равно h+1 ;

$C*=[C_0 C_1 \dots C_h]$

где в роли блоков выступают матрицы размерности $m \times n$ , а число блочных столбцов равно h+1 ;

$G_i*=[G_I^{(0)} G_i^{(1)} \dots G_i^{(h)}$

где в роли блоков выступают матрицы размерности $m \times n$ , а число блочных столбцов равно h +1 ;

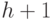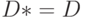
В справедливости (22.6) и (22.7) можно убедиться, выполнив непосредственную подстановку. Поскольку соответствующие выкладки являются громоздкими, но не представляют принципиальной сложности, здесь они не приводятся.

Рассмотрим билинейный автомат с распределенным запаздыванием по управлению.

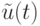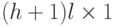Пусть входным вектором в момент времени является $\tilde (t)=[\bar u(t) \bar u(t-1) \dots \bar u(t-h)]^T$ . Тогда размерность $\tilde u(t)$ равна $(h+1)l \times 1$ .

Начальный входной вектор $\tilde u(0)=[\bar u(0) \bar u(-1) \dots \bar u(-h)]^T$ .

Тогда билинейный автомат с распределенным запаздыванием по управлению можно описать следующим образом:

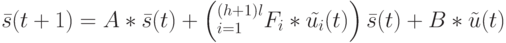$\bar s(t+1)=A*\bar s(t)+ \left (\suim_{i=1}^{(h+1)l}F_i* \tilde {u_i}(t) \right ) \bar s(t)+B* \tilde u(t)$

( 22.8)

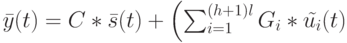$\bar y(t)=C*\bar s(t)+ \left (\sum_{i=1}^{(h+1)l}G_i* \tilde {u_i}(t)$

( 22.9)

Здесь

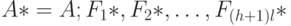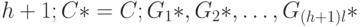$A*=A; F_1*, F_2*, \dots , F_{(h+1)l}*$ равны соответственно $F_1^{(0)}, \dots , F_l^{(0)}, \dots , F_1^{(h)}, \dots , F_l^{(h)}; B*=[B_0 B_1 \dots B_h]$ - вектор блочной структуры, где в роли блоков выступают матрицы размерности $n \times l$ , а число блочных столбцов равно $h+1; C*=C; G_1*, G_2*, \dots, G_{(h+1)l}*$ равны соответственно $G_1^{(0)}, \dots , G_l^{(0)}, \dots , G_1^{(h)}, \dots, G_l^{(h)}, D*=[D_0 D_1 \dots D_h]$ - вектор блочной структуры, где в роли блоков выступают матрицы размерности $m \times l$ , а число блочных столбцов равно h+1 .

В справедливости (22.8) и (22.9) можно убедиться, выполнив непосредственную подстановку.

В результате предложенных выше преобразований исходный билинейный автомат с распределенным запаздыванием по состоянию (по управлению) сведен к билинейному автомату без запаздывания, вектор состояния (входной вектор) которого имеет большую размерность, чем исходный автомат. Последнее означает, что с точки зрения функционального поведения оба эти автомата являются эквивалентными.

Приведенные ниже теоремы являются аналогами доказанных выше теорем 12.1, 12.4, 12.5 и т. д.

Теорема 22.5. Для того чтобы входная последовательность $\bar u(0) \dots \bar u(t)$ была синхронизирующей для билинейного автомата $\tilde A$ с распределенным запаздыванием по состоянию, необходимо и достаточно, чтобы выполнялось равенство

$\Pi_{\nu =0}^t \left [ \begin {matrix} A_0+\sum_{i=1}^lF_i^{(0)}u_i(t- \nu)& A_1+\sum_{i=1}^lF_i^{(1)}u_i(t- \nu) & \dots & A_h+\sum_{i=1}^lF_i^{(h)}u_i(t- \nu)\\ E_n& 0_n& \dots & 0_n\\ \dots & \dots & \dots & \dots \\ 0_n& \dots & E_n& 0_n \end {matrix} \right ] =[0]$

Теорема 22.6. Для того чтобы входная последовательность $\bar u(0) \dots \bar u(t)$ была синхронизирующей для билинейного автомата $\tilde A$ с распределенным запаздыванием по управлению, необходимо и достаточно, чтобы выполнялось равенство

$\Pi_{\nu =0}^{t}[A+\sum_{k=0}^h \sum_{i=1}^l F_i^{(k)} u_i(t-\nu)]=[0]$

Теорема 22.7. Для того чтобы входная последовательность $\bar u(0) \dots \bar u(t)$ была установочной для билинейного автомата $\tilde A$ с распределенным запаздыванием по состоянию, необходимо и достаточно, чтобы для каждого ненулевого состояния $\bar s \in S_{(h+1)n}$ выполнялось по крайней мере одно из условий:

$\wedge_{d=0}^t \left [ \begin {matrix} [C_0+\sum_{i=1}^lG_i^{(0)}u_i(d) \dots C_h+\sum_{i=1}^lG_i^{(h)}u_i(d)] \times \\ \Pi_{\nu =0}^{d-1} \left [ \begin {matrix} A_0+\sum_{i=1}^lF_i^{(0)}u_i(d-\nu -1)& \dots &\dots & A_h+\sum_{i=1}^lF_i^{(h)}u_i(d- \nu -1)\\ E_n& 0_n& \dots & 0_n\\ \dots & \dots & \dots &\dots \\ 0_n & \dots & E_n& 0_n \end {matrix} \right ]\bar s \ne 0 \end {matrix} \right]$
$\Pi_{\nu =0}^t \left [ \begin {matrix} A_0+\sum_{i=1}^l F_i^{(0)}u_i(t- \nu)& A_1+\sum_{i=1}^lF_i^{(0)}u_i(t- \nu)& \dots A_h+\sum_{i=1}^lF_i^{(h)}u_i(t- \nu)\\ E_n& 0_n& \dots 0_n\\ \dots & \dots & \dots & \dots \\ 0_n& \dots E_n & 0_n \end {matrix} \right ]=\bar s=[0]$

Здесь знак $\wedge_{d=0}^{t}$ означает дизъюнкцию выражений, стоящих за этим знаком и получаемых при изменении индекса от 0 до .

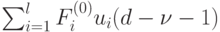Если при вычислениях индекс у u_i меньше нуля при некоторых и $\nu$ (условие 1), то выражение $\sum_{i=1}^lF_i^{(0)}u_i(d- \nu -1)$ положим равным единичной матрице.

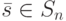Теорема 22.8. Для того чтобы входная последовательность $\bar u(0) \dots \bar u(t)$ была установочной для билинейного автомата $\tilde A$ с распределенным запаздыванием по управлению, необходимо и достаточно, чтобы для каждого ненулевого состояния $\bar s \in S_n$ выполнялось по крайней мере одно из условий:

$\wedge_{d=0}^t \left [ \left [ C+\sum_{k=0}^h \sum_{i=0}^l G_i^{(k)} u_i(d) \right ] \Pi_{\nu =0}^{d-1}[A+\sum_{k=0}^h \sum_{i=0}^l F_i^{(k)}u_i(d-\nu -1)]\bar s \ne [0] \right ]$
$\Pi_{\nu =0}^{t}[A+\sum_{k=0}^h \sum_{i=0}^lF_i^{(k)}u_i(t- \nu)]\bar s =[0]$ .

Здесь знак 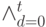$\wedge_{d=0}^t$ означает дизъюнкцию выражений, стоящих за этим знаком и получаемых при изменении индекса от 0 до .

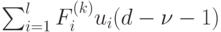Если при вычислениях индекс у u_i меньше нуля при некоторых и $\nu$ (условие 1), то выражение $\sum_{i=1}^lF_i^{(k)}u_i(d-\nu -1)$ положим равным единичной матрице.

Теорема 22.9. Для того чтобы входная последовательность $\bar u(0) \dots \bar u(t)$ была диагностической для билинейного автомата $\tilde A$ с распределенным запаздыванием по состоянию, необходимо и достаточно, чтобы

$rank \left [ \begin {matrix} \left [C_0+\sum_{i=1}lG_i^{(0)} \dots C_h+\sum_{i=1}^lG_i^{(h)}u_i(0) \right ]\\ \left [C_0+\sum_{i=1}^lG_i^{(0)}u_i(1) \dots C_h+\sum_{i=1}^lG_i^{(h)}u_i(1) \right ] \lefy (A*+\sum_{i=1}^lF_i*u_i(0) \right )\\ \left [ C_0+\sum_{i=1}^lG_i(0)u_i(t) \dots C_h+\sum_{i=1}^lG_i^{(h)}u_i(t) \right ] \Pi_{\nu =0}^{t} \left [A*+\sum_{i=1}^lF_i*u_i(t-\nu -1) \right ] \end {matrix} \right ]=(h+1)n$

Здесь матрицы со звездочкой имеют следующую блочную структуру:

$A*= \left [ \begin {matrix} A_0& A_1& \dots &A_h\\ E_n& 0_n& \dots 0_n\\ \dots & \dots & \dots & \dots \\ 0_n& \dots E_n& 0_n \end {matrix} \right ]$

где в роли блоков выступают матрицы размерности $n \times n$ , а число блочных строк и столбцов равно h+1 ;

$F_i*= \left [ \begin {matrix} F_I^{(0)}& F_i^{(1)} & \dots F_i^{(h)}\\ 0_n& 0_n& \dots 0_n\\ \dots & \dots & \dots & \dots \\ 0_n& 0_n& \dots 0_n \end {matrix} \right ]$

где в роли блоков выступают матрицы размерности $n \times n$ , а число блочных строк и столбцов равно h+1 .

Теорема 22.10. Для того чтобы входная последовательность $\bar u(0) \dots \bar u(t)$ была диагностической для билинейного автомата $\tilde A$ с распределенным запаздыванием по управлению, необходимо и достаточно, чтобы

$rank \left [ \begin {matrix} C+\sum_{k=0}^h \sum_{i=0}^lG_i^{(k)}u_i(0)\\ \left (C+\sum_{k=0}^h \sum_{i=0}^lG_i^{(k)}u_i(1) \right ) \left (A+\sum_{k=0}^h \sum_{i=0}^lF_i^{(k)}u_i(0) \right )\\ \left (C+\sum_{k=0}^h \sum_{i=0}^lG_i^{(k)}u_i(t) \right ) \Pi_{\nu = 0}^t \left [A+\sum_{k=0}^h \sum_{i=0}^lF_i^{(k)}u_i(t-\nu -1) \right ] \end {matrix} \right ]=n$

Вопросы и упражнения

Дайте определение билинейного автомата без потери информации из некоторого состояния.
Дайте определение билинейного автомата без потери информации.
Сформулируйте условие принадлежности автомата классу билинейных автоматов БПИ.
Приведите определения билинейных автоматов с распределенным запаздыванием и просто с запаздыванием по состоянию и управлению.
Покажите, что билинейный автомат с распределенным запаздыванием всегда можно преобразовать в билинейный автомат без запаздывания.
Приведите критерии существования синхронизирующей, установочной и диагностической последовательностей для билинейных автоматов с распределенным запаздыванием.

Дальше >>

Теория экспериментов с конечными автоматами

Теория экспериментов с конечными автоматами

Разновидности экспериментов с билинейными автоматами

Вопросы и упражнения

Вопросы и ответы

Студенты

Авторизоваться

Теория экспериментов с конечными автоматами

Теория экспериментов с конечными автоматами

Разновидности экспериментов с билинейными автоматами

Вопросы и упражнения

Вопросы и ответы

Студенты