| Россия |
Установочные и диагностические эксперименты со стационарными и нестационарными линейными автоматами
Синхронизирующие, установочные и диагностические эксперименты с нестационарными линейными автоматами
Конкретизируем определение 1.1 синхронизирующей последовательности применительно к нестационарному ЛА: последовательность 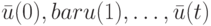 является СП для НЛА
является СП для НЛА  , если
, если
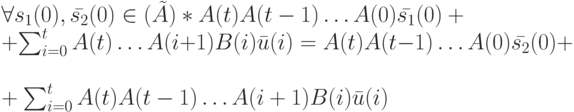
В этом определении  означает множество допустимых начальных состояний ЛА.
означает множество допустимых начальных состояний ЛА.
Теорема 11.9. Для того чтобы входная последовательность 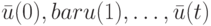 была СП для НЛА
была СП для НЛА  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
![\forall \bar {s_1}(0), s_2(0) \in \Init(\tilde A) A(t)A(t-1)\dots A(0)[\bar {s_1}(0)-\bar {s_2}(0)]=[0]](/sites/default/files/tex_cache/b96f205d37cfbf02bb959280faaf8cb4.png) |
( 11.10) |
Доказательство получается путем переноса в левую часть всех членов равенства в приведенном определении СП.
Следствие 1. Если 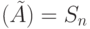 , то необходимым и достаточным условием существования СП длины
, то необходимым и достаточным условием существования СП длины  для НЛА является выполнение равенства
для НЛА является выполнение равенства
![A(t)A(t-1)\dots A(0)=[0]](/sites/default/files/tex_cache/a31a4136a3069858ed9fea11d3b45457.png) |
( 11.11) |
Доказательство. В силу произвольности начальных состояний  и
и  разность
разность 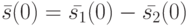 пробегает все множество состояний
пробегает все множество состояний 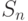 , следовательно, (11.10) можно переписать так:
, следовательно, (11.10) можно переписать так:
![\forall \bar s(0) \in S_n A(t)A(t-1) \dots A(0) \bar s(0)=[0]](/sites/default/files/tex_cache/ff1911713956864a210f02c61510a63f.png)
Понятно, что последнее справедливо тогда и только тогда, когда справедливо (11.11).
Следствие 2. Если  и для НЛА существует хотя бы одна СП длины
и для НЛА существует хотя бы одна СП длины  , то для него синхронизирующей является любая входная последовательность длины
, то для него синхронизирующей является любая входная последовательность длины  и более.
и более.
Справедливость этого утверждения вытекает из того, что условие (11.11) не зависит от входной последовательности.
Исследуем теперь вопрос об оценке длины СП для НЛА.
Рассмотрим НЛА  со следующими главными характеристическими матрицами:
со следующими главными характеристическими матрицами:
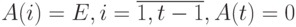
Очевидно, что для этого НЛА, как это вытекает из (11.11), СП имеет длину  и для него не существует СП меньшей длины. В силу произвольности параметра
и для него не существует СП меньшей длины. В силу произвольности параметра  отсюда следует, что в общем случае длина минимальной СП для НЛА не ограничена сверху. Напомним, что в отличие от НЛА для стационарных ЛА верхняя граница длины минимальных СП, как было показано выше, не превосходит величины
отсюда следует, что в общем случае длина минимальной СП для НЛА не ограничена сверху. Напомним, что в отличие от НЛА для стационарных ЛА верхняя граница длины минимальных СП, как было показано выше, не превосходит величины  , где
, где  - размерность ЛА.
- размерность ЛА.
Поскольку в общем случае задание НЛА требует перечисления бесконечных последовательностей характеристических матриц, что не всегда можно сделать конструктивно, рассмотрим специальный класс НЛА, описываемый конечными множествами таких матриц. НЛА этого класса назовем периодическими и потребуем, чтобы периодическими были все его характеристические матрицы. Последнее означает, что существует такая целая положительная константа  , что
, что 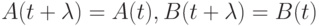 и т. д.
и т. д.
Перейдем теперь к исследованию условий существования СП периодических НЛА. Построим по периодической НЛА  стационарный ЛА, обозначаемый как
стационарный ЛА, обозначаемый как 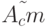 , у которого функция переходов имеет вид
, у которого функция переходов имеет вид
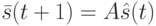
где
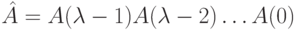
Теорема 11.10. СП для периодической НЛА  существует тогда и только тогда, когда она существует для стационарного ЛА
существует тогда и только тогда, когда она существует для стационарного ЛА 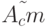
Доказательство.
Необходимость. Пусть для НЛА  существует СП минимальной длины
существует СП минимальной длины 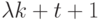 где
где  . Тогда по следствию 1 из теоремы 11.9 должно выполняться равенство
. Тогда по следствию 1 из теоремы 11.9 должно выполняться равенство
![A(\lambda k+t)A(\lambda k+t-1)\dots A(\lambda )A(\lambda -1)\dots A(0)=[0]](/sites/default/files/tex_cache/68ef028a34240664475da34707d1e42e.png)
В силу периодичности матрицы 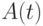 последнее равенство эквивалентно равенству
последнее равенство эквивалентно равенству
![A(t)A(t-1)\dots A(0) \hat {A^k}=[0]](/sites/default/files/tex_cache/a84963860d08e6f839b327cbe53c17c6.png)
Отсюда вытекает, что ![\hat {A^k}=[0]](/sites/default/files/tex_cache/a5088103a1fb074385481c4c5050d945.png) но по теореме 1.1 это есть необходимое и достаточное условие существования СП для стационарного ЛА
но по теореме 1.1 это есть необходимое и достаточное условие существования СП для стационарного ЛА 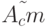
Достаточность. Пусть для линейного автомата 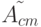 существует СП длины
существует СП длины  тогда должно выполняться условие
тогда должно выполняться условие  Отсюда следует, что
Отсюда следует, что

Тогда, в силу справедливости (1.28), для НЛА  существует СП длина
существует СП длина 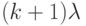
Теорема 11.11. Если  - период главной характеристической матрицы
- период главной характеристической матрицы 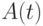 НЛА
НЛА  , то длина минимальной СП не превосходит величины
, то длина минимальной СП не превосходит величины 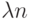 , где
, где  - размерность НЛА.
- размерность НЛА.
Справедливость этой теоремы вытекает из того, что длина минимальной СП стационарного ЛА размерности  , как было показано выше, не превосходит величины
, как было показано выше, не превосходит величины  .
.
Конкретизируем теперь определение 1.2 установочной последовательности применительно к нестационарному ЛА: последовательность 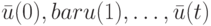 является УП для НЛА
является УП для НЛА  , если
, если
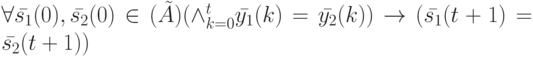
где  - символ конкатенации
- символ конкатенации  равенств,
равенств,  - выходная реакция и состояние автомата в момент времени , стартующего из состояния
- выходная реакция и состояние автомата в момент времени , стартующего из состояния 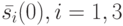
Теорема 11.12. Для того чтобы входная последовательность 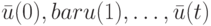 являлась УП для НЛА
являлась УП для НЛА  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
![\forall \bar {s_1}(0), \bar {s_2}(0) \in \Init (\tilde A)\\
\exists k \in [0:t] (C(k)A(k-1) \dots A(0)[\bar {s_1}(0)- \bar {s_2}(0) \ne [0]) \vee\\
\vee (A(t)A(t-1) \dots A(0)[\bar {s_1}(0)- \bar {s_2}(0)=[0])](/sites/default/files/tex_cache/a02af08371a85934d6311cbd6b413c8f.png) |
( 11.12) |
Доказательство. Перепишем приведенное выше определение УП для НЛА в терминах характеристических матриц:
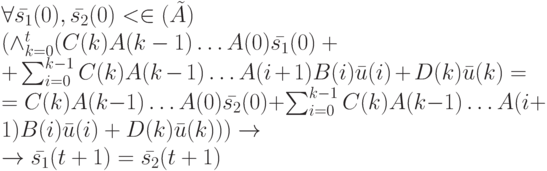
Выполнив преобразования выражения, стоящего после квантора общности, получим
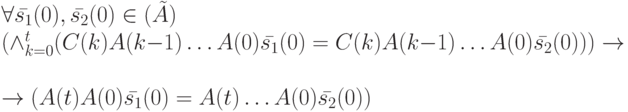
Учитывая, что 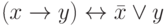 и
и  , из последнего соотношения получим
, из последнего соотношения получим
![\forall \bar {s_1}(0), \bar {s_2}(0) \in \Init (\tilde A)\\
\left ( \wedge_{k=0}^t C(k)A(k-1) \dots A(0)[\bar {s_1}(0)-\bar {s_2}(0)] =ne [0] \right ) \vee\\
\vee (A(t) \dots A(0)[\bar {s_1}(0)-\bar {s_2}(0)]=[0])](/sites/default/files/tex_cache/842811a053c76371c96530e2c7d53295.png)
Очевидно, что последний предикат эквивалентен предикату, приведенному в формулировке теоремы.
Заметим, что если 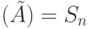 , то разность
, то разность ![[\bar {s_1}(0)-\bar {s_2}(0)]](/sites/default/files/tex_cache/15fc73d6b987a017048ce1ae35d8b863.png) пробегает все множество состояний
пробегает все множество состояний 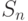 рассматриваемого НЛА
рассматриваемого НЛА 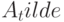 и в этом случае условие (11.12) принимает следующий вид:
и в этом случае условие (11.12) принимает следующий вид:
![\forall \bar s(0) \in S_n \exists k \in [0:t] (C(k)A(k-1) \dots A(0) \bar s (0) \ne [0]) \vee (A(t) \dots A(0)=[0])](/sites/default/files/tex_cache/dabc6bce1c9073cf4c8079a40e4d2747.png) |
( 11.13) |
Следствие. Если для НЛА  существует хотя бы одна УП длины
существует хотя бы одна УП длины  , то для него установочной является любая входная последовательность длины
, то для него установочной является любая входная последовательность длины  и более.
и более.
Справедливость этого утверждения вытекает из того, что предикат (11.13) не зависит от входной последовательности.
Поскольку СП есть частный случай УП, то в общем случае длина минимальной УП для НЛА есть величина, не ограниченная сверху. Что касается периодического НЛА  , то для оценки длины минимальной УП справедлив аналог теоремы 1.14, т. е. эта длина не превосходит величины
, то для оценки длины минимальной УП справедлив аналог теоремы 1.14, т. е. эта длина не превосходит величины 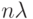 , где
, где  - размерность НЛА,
- размерность НЛА,  - период матрицы
- период матрицы 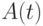 .
.
Обратимся теперь к исследованию условия существования для НЛА диагностической последовательности.
Определение ДП для НЛА можно представить так: последовательность 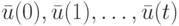 является ДП для НЛА
является ДП для НЛА  , если
, если
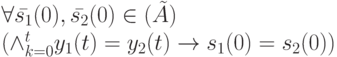
Используемые здесь обозначения совпадают с теми, что были приведены выше в определении УП.
По аналогии со стационарным ЛА введем в рассмотрение следующую матрицу, которую будем называть диагностической матрицей для НЛА:
![K_t=
\left [
\begin {matrix}
C(0)\\
C(1)A(0)\\
C(2)A(1)A(0)\\
……………….\\
C9t)A(t-1)A(t-2) \dots a(0)
\end {matrix}
\right ]](/sites/default/files/tex_cache/aeb0cb6c079706200ddadf812ea6db6c.png)
Теорема 11.13. Для того чтобы для НЛА  размерности
размерности  , у которого
, у которого 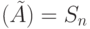 , входная последовательность
, входная последовательность 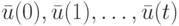 являлась ДП, необходимо и достаточно, чтобы
являлась ДП, необходимо и достаточно, чтобы 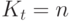 .
.
Доказательство. В терминах характеристических матриц приведенное только что определение ДП запишется следующим образом:

Выполнив простые преобразования и сокращения, в результате получим
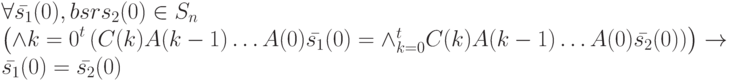
Обозначив разность  через
через  , последний предикат можно переписать в следующем виде:
, последний предикат можно переписать в следующем виде:

или, что все равно,
![\forall \bar s(0) \in S_n\\
K_t \bar s(0)=[0]](/sites/default/files/tex_cache/fb8ca22f171565c4951d4d701ffdd615.png)
Последнее соотношение, стоящее под знаком квантора общности, можно трактовать как систему линейных однородных алгебраических уравнений относительно координат вектора  . Существование ДП для НЛА равносильно тому, что соответствующая система имеет единственное решение. Из алгебры известно, что необходимым и достаточным условием для этого является выполнение равенства
. Существование ДП для НЛА равносильно тому, что соответствующая система имеет единственное решение. Из алгебры известно, что необходимым и достаточным условием для этого является выполнение равенства 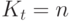 .
.
Следствие. Если для НЛА существует ДП длины  , то для него диагностической является любая входная последовательность длины
, то для него диагностической является любая входная последовательность длины  и более.
Справедливость этого утверждения вытекает из того, что условие теоремы 11.13 не зависит от входной последовательности.
и более.
Справедливость этого утверждения вытекает из того, что условие теоремы 11.13 не зависит от входной последовательности.
Понятно, что всякая ДП для НЛА одновременно является и УП для этого автомата. Вместе с тем, в общем случае не всякая УП для НЛА одновременно является и ДП. По этой причине все сказанное выше о верхней границе длины минимальной УП в полной мере относится и к верхней границе ДП.
Подведем некоторые итоги исследования экспериментов как для стационарных, так и нестационарных автоматов.
Представленные в первых двух разделах лекции результаты свидетельствуют о том, что специфика линейных автоматов существенно упрощает построение теории экспериментов для них. Так, эта специфика дает возможность значительно понизить верхние оценки длин минимальных экспериментов всех типов по сравнению с соответствующими оценками, известными для автоматов (в общем случае нелинейных) Мили. Кроме того, эта специфика позволяет свести задачу построения рассмотренных экспериментов, в общем случае весьма сложную и трудоемкую, к значительно более простой задаче установления факта существования таких экспериментов. Решение же последней задачи требует лишь вычисления произведения некоторых характеристических матриц, либо степеней матриц и их рангов. Иными словами, условия существования экспериментов исследованных нами типов для линейных автоматов достаточно легко проверяются. Отметим еще одно важное обстоятельство: идентификация финальных и начальных состояний после проведения соответствующих типов экспериментов в случае линейных автоматов сводится к решению систем линейных алгебраических уравнений, для чего имеется хорошо разработанный математический аппарат.
Вопросы и упражнения
- Сформулируйте критерии существования установочной последовательности для линейного стационарного автомата.
- При каких ограничениях на характеристическую матрицу С линейного стационарного автомата все входные последовательности некоторой фиксированной длины являются для него установочными?
- Какова верхняя оценка длины минимальной установочной последовательности для стационарного линейного автомата?
- Сформулируйте критерии существования диагностической последовательности для линейного стационарного автомата.
- Какова верхняя оценка длины минимальной диагностической последовательности для стационарного линейного автомата?
- Является ли условие минимальности стационарного ЛА достаточным для существования у него диагностической последовательности?
- Приведите доказательство того, что для стационарного ЛА с помощью простого безусловного эксперимента разрешима любая диагностическая задача.
- Дайте определение периодического линейного нестационарного автомата.
- Сформулируйте критерии существования синхронизирующей, установочной и диагностической последовательностей для периодического линейного нестационарного автомата.


 - единичная
- единичная