| Россия |
Синхронизирующие эксперименты с линейными автоматами
Условия существования синхронизирующей последовательности
Приведенное выше определение СП применительно к ЛА формулируется следующим образом: входную последовательность  ЛА
ЛА  назовем СП, если
назовем СП, если
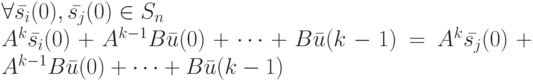 |
( 10.9) |
Перенося в (10.9) правую часть равенства влево, получим
![\forall \bar {s_j}(0), \bar {s_j}(0) \in S_n A^k(\bar {s_i}(0)-\bar {s_j}(0))=[0]](/sites/default/files/tex_cache/91a33c77c22117e39d495de584ed4728.png) |
( 10.10) |
Символом [0] здесь и далее обозначается нулевая матрица или нулевой вектор подходящей размерности.
Поскольку в (10.10)  и
и  есть произвольные состояния, то (10.10) эквивалентно предикату
есть произвольные состояния, то (10.10) эквивалентно предикату
![\forall \bar s \in S_n A^k \bar s=[0]](/sites/default/files/tex_cache/401f8f1d6fcb20440de1845b87ba11fa.png) |
( 10.11) |
Теорема 10.1. Для того чтобы ЛА  имел СП длины
имел СП длины  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы ![А^k=[0]](/sites/default/files/tex_cache/181f1fb0f564f90cf294481b151ac48c.png) .
.
Доказательство. Соотношение
![A^k\bar s=[0]](/sites/default/files/tex_cache/ae5aaa530d73795b7641488a09ba15f3.png) |
( 10.12) |
можно интерпретировать как систему линейных алгебраических уравнений (СЛАУ) относительно переменных 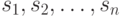 , являющихся координатами вектор-столбца
, являющихся координатами вектор-столбца  . Пусть ранг матрицы
. Пусть ранг матрицы  равен
равен  , где
, где  . Из алгебры известно, что в этом случае число свободных неизвестных
. Из алгебры известно, что в этом случае число свободных неизвестных 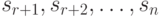 в системе (10.12) равно
в системе (10.12) равно  . Тогда переменные
. Тогда переменные 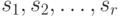 будут выражаться через свободные переменные и, следовательно, число решений системы равно
будут выражаться через свободные переменные и, следовательно, число решений системы равно 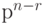 . Поскольку СП для ЛА существует тогда и только тогда, когда решением системы (10.12) является любой вектор
. Поскольку СП для ЛА существует тогда и только тогда, когда решением системы (10.12) является любой вектор 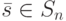 , где
, где  , то из сравнения
, то из сравнения  и
и 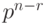 вытекает, что
вытекает, что  должно равняться нулю, т. е. ранг матрицы
должно равняться нулю, т. е. ранг матрицы  равен 0. Из последнего равенства следует, что
равен 0. Из последнего равенства следует, что ![А^k =[0]](/sites/default/files/tex_cache/ae3aed995ad225fbb0b288c130fadd4f.png) .
.
Определение 10.4. Линейный автомат  будем называть синхронизируемым, если у него существует СП.
будем называть синхронизируемым, если у него существует СП.
Из теоремы 10.1 вытекает следующее следствие.
Следствие. Для того чтобы ЛА  был синхронизируем, необходимо, чтобы его главная характеристическая матрица А была вырожденной.
был синхронизируем, необходимо, чтобы его главная характеристическая матрица А была вырожденной.
Доказательство. Пусть ЛА синхронизируем, тогда существует такое целое  , что
, что ![А^k = [0]](/sites/default/files/tex_cache/f5b142c66974af5110620c44e2776e12.png) . Это означает, что матрица
. Это означает, что матрица  является вырожденной. Из алгебры известно, что определитель произведения матриц равен произведению определителей. Отсюда следует, что
является вырожденной. Из алгебры известно, что определитель произведения матриц равен произведению определителей. Отсюда следует, что  , где
, где 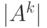 и
и 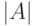 - определители матриц
- определители матриц 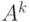 и
и  соответственно. Поскольку
соответственно. Поскольку ![А^k = [0]](/sites/default/files/tex_cache/f5b142c66974af5110620c44e2776e12.png) , то
, то 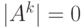 , но
, но  , следовательно
, следовательно  .Отсюда следует, что
.Отсюда следует, что 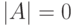 , т. е. матрица
, т. е. матрица  является вырожденной.
является вырожденной.
Теорема 10.2. Если для ЛА  существует хотя бы одна СП длины
существует хотя бы одна СП длины  , то для этого автомата синхронизирующими являются любые входные последовательности длины
, то для этого автомата синхронизирующими являются любые входные последовательности длины  и более.
и более.
Доказательство. Из теоремы 10.1 следует, что для ЛА, имеющего СП 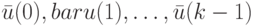 длины
длины  , конечное состояние ЛА после подачи СП выражается по формуле (10.3) следующим образом:
, конечное состояние ЛА после подачи СП выражается по формуле (10.3) следующим образом:
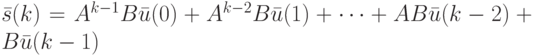 |
( 10.13) |
Поскольку правая часть последнего равенства не зависит от начального состояния  ЛА, это означает, что при любом начальном состоянии некоторая фиксированная входная последовательность
ЛА, это означает, что при любом начальном состоянии некоторая фиксированная входная последовательность 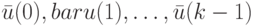 переводит ЛА в одно и то же конечное состояние. Этот факт остается справедливым и для любой другой фиксированной входной последовательности. Иными словами, любая входная последовательность длины
переводит ЛА в одно и то же конечное состояние. Этот факт остается справедливым и для любой другой фиксированной входной последовательности. Иными словами, любая входная последовательность длины  является для этого ЛА синхронизирующей. Ясно, что и любая входная последовательность большей длины также будет синхронизирующей.
является для этого ЛА синхронизирующей. Ясно, что и любая входная последовательность большей длины также будет синхронизирующей.
Заметим, что последняя теорема свидетельствует о принципиальном различии между общими автоматами Мили и линейными автоматами с точки зрения возможности их синхронизации. Если для некоторого автомата Мили СП длины  существует, то общее их число может быть невелико. В частности, автомат Мили может иметь одну единственную СП. В то же время для ЛА существование одной СП длины
существует, то общее их число может быть невелико. В частности, автомат Мили может иметь одну единственную СП. В то же время для ЛА существование одной СП длины  автоматически влечет существование
автоматически влечет существование 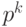 СП такой же длины.
СП такой же длины.
Обратимся теперь к вопросу о том, как практически установить существование у заданного ЛА СП и если таковая существует, то как найти длину минимальной СП. Из теории автоматов известно, что установочная задача для автомата с  состояниями и с
состояниями и с  допустимыми начальными состояниями всегда может быть решена с помощью простого безусловного эксперимента длины
допустимыми начальными состояниями всегда может быть решена с помощью простого безусловного эксперимента длины  , где
, где 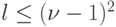 . Задача синхронизации автомата является, очевидно, частным случаем установочной задачи. Используя этот факт, для установления факта существования СП необходимо вычислять последовательно степени
. Задача синхронизации автомата является, очевидно, частным случаем установочной задачи. Используя этот факт, для установления факта существования СП необходимо вычислять последовательно степени  главной характеристической матрицы ЛА для
главной характеристической матрицы ЛА для 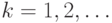 , до тех пор, пока на очередном шаге она не выродится в нулевую. Очевидно, что наименьшее целое k такое, для которого
, до тех пор, пока на очередном шаге она не выродится в нулевую. Очевидно, что наименьшее целое k такое, для которого ![А^k=[0]](/sites/default/files/tex_cache/181f1fb0f564f90cf294481b151ac48c.png) , равно длине минимальной СП. Если же в процессе вычисления окажется, что
, равно длине минимальной СП. Если же в процессе вычисления окажется, что ![А^k \ne [0]](/sites/default/files/tex_cache/53e73b511a0d9ed2b9f229a8a8230810.png) при
при 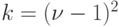 , где
, где  - размерность ЛА, то СП для этого ЛА не существует и на этом процесс вычисления степеней матриц прекращается.
- размерность ЛА, то СП для этого ЛА не существует и на этом процесс вычисления степеней матриц прекращается.
Упомянутая выше верхняя граница длины минимальной СП, равная величине 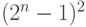 , достаточно велика. Укажем один частный вид ЛА, для которого эта верхняя граница существенно ниже.
, достаточно велика. Укажем один частный вид ЛА, для которого эта верхняя граница существенно ниже.
Назовем квадратную матрицу верхней (нижней) треугольной, если все ее элементы, лежащие на главной диагонали и ниже (выше) нее, равны нулю.
Теорема 10.3. Если главная характеристическая матрица ЛА размерности n является верхней (нижней) треугольной, то длина минимальной СП для этого ЛА не превосходит  .
.
Доказательство. Проведем его для верхней треугольной матрицы, которую обозначим через А:
![\left [
\begin {matrix}
0&a_{12}&a_{13}&\dots &a_{1, n-1}&a_{1,n}\\
0&0&a_{23}& \dots &a_{2,n-1}& a_{2,n}\\
\dots & \dots & \dots & \dots & \dots & \dots\\
0& 0& 0& \dots & a_{n-2, n-1}& a_{n-2,n}\\
0 & 0 & 0 & \dots & 0 & a_{n-1, n}\\
0 & 0 & 0 & \dots & 0 & 0
\end {matrix}
\right ]](/sites/default/files/tex_cache/836f12c371b896d2c6c13bb87d8f2d4a.png)
Условимся нумеровать диагонали матрицы, параллельные ее главной диагонали и расположенные выше нее, в порядке убывания числа элементов в них. Тогда диагональ, содержащая элементы 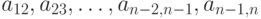 , получит номер 1, а диагональ, содержащая единственный элемент
, получит номер 1, а диагональ, содержащая единственный элемент 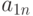 , - номер
, - номер  . Непосредственными вычислениями можно убедиться, что в матрице
. Непосредственными вычислениями можно убедиться, что в матрице 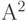 все элементы первой диагонали равны 0, в матрице
все элементы первой диагонали равны 0, в матрице 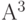 все элементы первой и второй диагонали также равны 0. Методом индукции можно доказать, что в матрице
все элементы первой и второй диагонали также равны 0. Методом индукции можно доказать, что в матрице  наряду с ее нулевой нижней треугольной подматрицей диагонали с номерами
наряду с ее нулевой нижней треугольной подматрицей диагонали с номерами 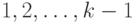 также содержат только нули. Из последнего утверждения следует, что по крайней мере в матрице
также содержат только нули. Из последнего утверждения следует, что по крайней мере в матрице 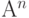 все элементы равны 0. Тогда на основании теоремы 10.1 рассматриваемый ЛА имеет СП, длина которой не превосходит
все элементы равны 0. Тогда на основании теоремы 10.1 рассматриваемый ЛА имеет СП, длина которой не превосходит  .
.
Для нижней треугольной матрицы соответствующее утверждение доказывается аналогично.
Ниже будет показано, что в действительности длина минимальной СП не превосходит  для произвольного синхронизируемого ЛА размерности
для произвольного синхронизируемого ЛА размерности  , а не только для частного вида ЛА, фигурирующего в теореме 10.3.
, а не только для частного вида ЛА, фигурирующего в теореме 10.3.
Состояние ЛА А, в котором он оказывается после подачи некоторой его СП, назовем синхросостоянием.
Обозначим через  множество всех возможных синхросостояний ЛА. Ясно, что в общем случае попарно различные СП могут переводить ЛА как в различные, так и в совпадающие синхросостояния, т. е.
множество всех возможных синхросостояний ЛА. Ясно, что в общем случае попарно различные СП могут переводить ЛА как в различные, так и в совпадающие синхросостояния, т. е.  .
.
Рассмотрим следующую задачу. Пусть задан синхронизируемый ЛА  , синхросостояние
, синхросостояние 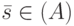 и пусть
и пусть  - длина минимальной СП этого автомата. Требуется найти такую входную последовательность длины
- длина минимальной СП этого автомата. Требуется найти такую входную последовательность длины  , которая переводит ЛА
, которая переводит ЛА  в синхросостояние
в синхросостояние  .
.
Для рассматриваемого ЛА выражение (10.13) можно переписать в виде
 |
( 10.14) |
Далее (10.14) будем рассматривать как СЛАУ (неоднородных) относительно неизвестных 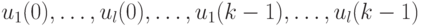 , общее число которых равно
, общее число которых равно  .
.
Пусть ![Q = [q_{ij}]_{n x lk}](/sites/default/files/tex_cache/b4c46ff79e9285692c6f8102707a2c5b.png) есть матрица системы (10.14), а
есть матрица системы (10.14), а 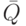 есть расширенная (добавлением к матрице
есть расширенная (добавлением к матрице  столбца
столбца  ) матрица той же системы и
) матрица той же системы и 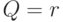 . Необходимым и достаточным условием совместности системы (10.14) является, как известно из алгебры, условие rank
. Необходимым и достаточным условием совместности системы (10.14) является, как известно из алгебры, условие rank  (теорема Кронекера - Капелли). Понятно, что для выполнения этого условия вектор-столбец
(теорема Кронекера - Капелли). Понятно, что для выполнения этого условия вектор-столбец  должен быть линейной комбинацией
должен быть линейной комбинацией  линейно независимых столбцов матрицы
линейно независимых столбцов матрицы  . Иными словами, только для вектор-столбцов
. Иными словами, только для вектор-столбцов  , представляющих собой такие комбинации, соответствующая СП может быть найдена. Ясно, что если для некоторого
, представляющих собой такие комбинации, соответствующая СП может быть найдена. Ясно, что если для некоторого  система (10.14) оказывается несовместной, это означает, что заданное
система (10.14) оказывается несовместной, это означает, что заданное  не принадлежит множеству синхросостояний
не принадлежит множеству синхросостояний  .
.
Напомним, как могут быть найдены решения системы (10.14) в случае ее совместности. С этой целью выберем в матрице 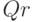 линейно независимых строк и в (10.14) оставим лишь те уравнения, коэффициенты которых вошли в выбранные строки. В левых частях этих уравнений оставляем такие
линейно независимых строк и в (10.14) оставим лишь те уравнения, коэффициенты которых вошли в выбранные строки. В левых частях этих уравнений оставляем такие  неизвестных, что определитель из коэффициентов при них отличен от нуля. Остальные неизвестные в этих уравнениях объявляем свободными и переносим в правые части уравнений. Варьируя значения свободных переменных (все они являются элементами поля
неизвестных, что определитель из коэффициентов при них отличен от нуля. Остальные неизвестные в этих уравнениях объявляем свободными и переносим в правые части уравнений. Варьируя значения свободных переменных (все они являются элементами поля  ) и вычисляя значения остальных неизвестных (например, по правилу Крамера), получим все решения системы (10.14).
) и вычисляя значения остальных неизвестных (например, по правилу Крамера), получим все решения системы (10.14).
Проиллюстрируем сказанное на примере. Пусть ЛА над полем  задан характеристическими матрицами:
задан характеристическими матрицами:
![A=
\left [
\begin {matrix}
0& 0& 0& 0\\
1& 0& 0& 0\\
1& 1& 0& 0\\
1& 1& 1& 0
\end {matrix}
\right ],\\
b=
\left [
\begin {matrix}
1& 1\\
1& 1\\
1& 1\\
1&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/b89b38f06fada8be0cc273cac84ff186.png)
где 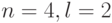 , тогда
, тогда ![\bar u=[u_1, u_2]'](/sites/default/files/tex_cache/93736b7046446c4f581133a09c4d631b.png) .
.
По теореме 10.3 этот ЛА синхронизируем и длина его минимальной СП равна 4. Система (10.14) в нашем случае в матричной форме имеет вид
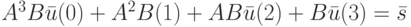 |
( 10.15) |
Вычислим матрицы  :
:
![A^3B=
\left [
\begin {matrix}
0&0\\
0&0\\
0&0\\
1&1
\end {matrix}
\right ],\\
A^2B=
\left [
\begin {matrix}
0&0\\
0&0\\
1&1\\
1&1
\end {matrix}
\right ],\\
AB=
\left [
\begin {matrix}
0&0\\
1&1\\
0&0\\
1&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/9652ea011d710e18c09915432dc6a682.png)
Используя эти матрицы, перепишем систему уравнений (10.15) в координатной форме, где неизвестными являются 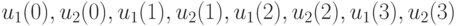 - координаты векторов
- координаты векторов 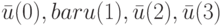 :
:
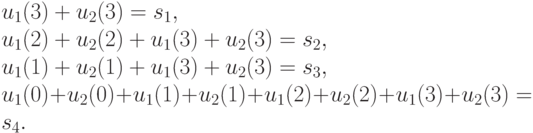 |
( 10.16) |
Здесь 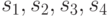 есть координаты вектора
есть координаты вектора  .
.
Матрица этой системы имеет вид
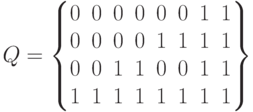
Вычисления показывают, что 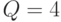 . Перенумеруем столбцы матрицы
. Перенумеруем столбцы матрицы  слева направо начиная с 1. Выберем в
слева направо начиная с 1. Выберем в  четыре линейно независимых столбца, например, с номерами 1, 3, 5, 7, которым соответствуют неизвестные
четыре линейно независимых столбца, например, с номерами 1, 3, 5, 7, которым соответствуют неизвестные 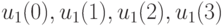 . Легко проверить, что определитель, составленный из названных столбцов, отличен от нуля. Оставим эти перечисленные неизвестные в левых частях уравнений системы (10.16), а остальные переменные объявим свободными и перенесем в правые части уравнений:
. Легко проверить, что определитель, составленный из названных столбцов, отличен от нуля. Оставим эти перечисленные неизвестные в левых частях уравнений системы (10.16), а остальные переменные объявим свободными и перенесем в правые части уравнений:
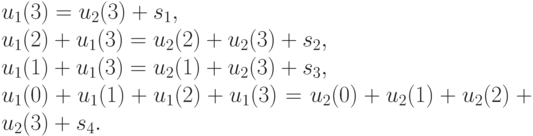
После простых и очевидных преобразований последняя система примет вид
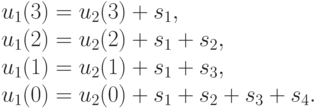 |
( 10.17) |
Выберем, например, состояние 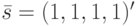 и проверим, является ли оно синхросостоянием. Если да, то найдем минимальную по длине СП, переводящую заданный ЛА в это синхросостояние. Условимся также среди всех минимальных по длине СП найти такую, которая имеет минимальный вес. Весом СП назовем число, которое равно сумме координат входных символов, составляющих эту СП.
и проверим, является ли оно синхросостоянием. Если да, то найдем минимальную по длине СП, переводящую заданный ЛА в это синхросостояние. Условимся также среди всех минимальных по длине СП найти такую, которая имеет минимальный вес. Весом СП назовем число, которое равно сумме координат входных символов, составляющих эту СП.
Поскольку в нашем примере 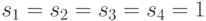 , то система (10.17) примет вид:
, то система (10.17) примет вид:
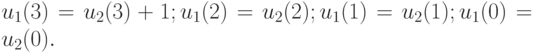
Для получения искомой СП минимального веса положим 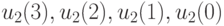 равными нулю. Тогда искомая СП, переводящая заданный ЛА из любого состояния в состояние
равными нулю. Тогда искомая СП, переводящая заданный ЛА из любого состояния в состояние  , такова:
, такова: 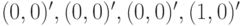 .
.
Вопросы и упражнения
- Опишите состав и устройство линейного автомата.
- Приведите системы уравнений состояний и выходов, описывающих функционирование стационарных (нестационарных) линейных автоматов.
- Приведите формулы для определения конечного состояния и реакции стационарного (нестационарного) линейного автомата при подаче на него последовательности входных символов.
- Дайте определения синхронизирующих, установочных и диагностических последовательностей и поясните их содержательный смысл.
- Сформулируйте критерий существования синхронизирующих последовательностей для стационарных линейных автоматов.
- Охарактеризуйте свойства синхронизирующих последовательностей.
- Сформулируйте постановку задачи перевода линейного автомата в заданное синхросостояние.
- Опишите метод решения задачи перевода линейного автомата в заданное синхросостояние.
-
ЛА над полем
 задан следующими характеристическими матрицами:
задан следующими характеристическими матрицами: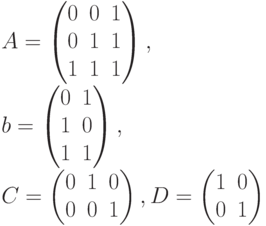
Требуется проверить, существует ли для этого ЛА синхронизирующая (установочная, диагностическая) последовательность.
-
ЛА над полем
 имеет следующие характеристические матрицы:
имеет следующие характеристические матрицы: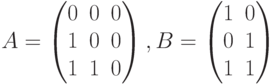
Покажите, что этот ЛА является синхронизируемым и найдите длину минимальной СП.
Проверьте, является ли состояние
![s=[1,1,1]'](/sites/default/files/tex_cache/7558cbabf32791c8b7f12935f28a4fb4.png) этого ЛА синхросостоянием, и если да, то найдите минимальную СП, переводящую ЛА в это состояние.
этого ЛА синхросостоянием, и если да, то найдите минимальную СП, переводящую ЛА в это состояние.
