Лекция 8: Организация таблиц символов
Таблицы расстановки со списками
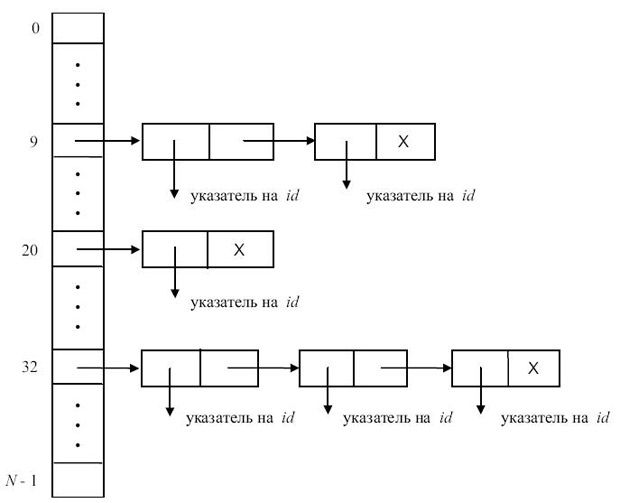
Только что описанная схема страдает одним недостатком - возможностью переполнения таблицы. Рассмотрим ее модификацию, когда все элементы, имеющие одинаковое значения (первичной) функции расстановки, связываются в список (при этом отпадает необходимость использования функций hi для i >= 2 ). Таблица расстановки со списками - это массив указателей на списки элементов ( рис. 7.3)
Вначале таблица расстановки пуста (все элементы имеют значение NULL ). При поиске идентификатора Id вычисляется функция расстановки h(Id) и просматривается соответствующий линейный список. Поиск в таблице может быть описан следующей функцией:
struct Element
{String IdentP;
struct Element * Next;
};
struct Element * T[N];
struct Element * Search(String Id)
{struct Element * P;
P=T[h(Id)];
while (1)
{if (P==NULL) return(NULL);
else if (IdComp(P->IdentP,Id)==0) return(P);
else P=P->Next;
}
}Занесение элемента в таблицу можно осуществить следующей функцией:
struct Element * Insert(String Id)
{struct Element * P,H;
P=Search(Id);
if (P!=NULL) return(P);
else {H=H(Id);
P=alloc(sizeof(struct Element));
P->Next=T[H];
T[H]=P;
P->IdentP=Include(Id);
}
return(P);
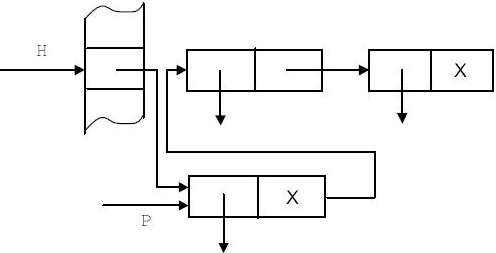
}Процедура Include заносит идентификатор в таблицу идентификаторов. Алгоритм иллюстрируется рис. 7.4.
Функции расстановки
Много внимания исследователями было уделено тому, какой должна быть (первичная) функция расстановки. Основные требования к ней очевидны: она должна легко вычисляться и распределять равномерно. Один из возможных подходов здесь заключается в следующем.
- По символам строки s определяем положительное целое H. Преобразование одиночных символов в целые обычно можно сделать средствами языка реализации. В Паскале для этого служит функция ord, в Си при выполнении арифметических операций символьные значения трактуются как целые.
- Преобразуем H, вычисленное выше, в номер элемента, то есть целое между 0 и N - 1, где N - размер таблицы расстановки, например, взятием остатка при делении H на N. Функции расстановки, учитывающие все символы строки, распределяют лучше, чем функции, учитывающие только несколько символов, например, в конце или середине строки. Но такие функции требуют больше вычислений. Простейший способ вычисления H - сложение кодов символов. Перед сложением с очередным символом можно умножить старое значение H на константу q. То есть полагаем H0 = 0, Hi = q*Hi-1 + ci для 1 <= i <= k, k - длина строки. При q = 1 получаем простое сложение символов. Вместо сложения можно выполнять сложение ci и q *Hj-1 по модулю
- Переполнение при выполнении арифметических операций можно игнорировать. Функция Hashpjw, приведенная ниже [?], вычисляется, начиная с H = 0 (предполагается, что используются 32- битовые целые). Для каждого символа c сдвигаем биты H на 4 позиции влево и добавляем очередной символ. Если какой- нибудь из четырех старших бит H равен 1, сдвигаем эти 4 бита на 24 разряда вправо, затем складываем по модулю 2 с H и устанавливаем в 0 каждый из четырех старших бит, равных 1.
#define PRIME 211
#define EOS '\0'
int Hashpjw(char *s)
{char *p;
unsigned H=0, g;
for (p=s; *p!=EOS; p=p+1)
{H=(H<<4)+(*p);
if (g=H&0xf0000000)
{H=H^(g>>24);
H=H^g;
} }
return H%PRIME;
}