Синтаксический анализ
Теорема 4.1. Язык допускается МП-автоматом тогда и только тогда, когда он допускается (некоторым другим автоматом) опустошением магазина.
Доказательство. Пусть L = L(M) для некоторого МП-
автомата 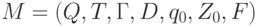 . Построим новый МП-
автомат M', допускающий тот же язык опустошением
магазина.
. Построим новый МП-
автомат M', допускающий тот же язык опустошением
магазина.
Пусть  где функция переходов D' определена следующим образом:
где функция переходов D' определена следующим образом:
- Если
 , то
, то  для всех
для всех  и
и 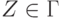 (моделирование М ),
(моделирование М ), -
 (начало работы),
(начало работы), - Для всех
 и
и  множество D'(q, e, Z)
содержит (qe, e) (переход в состояние сокращения
магазина без продвижения),
множество D'(q, e, Z)
содержит (qe, e) (переход в состояние сокращения
магазина без продвижения), -
D'(qe, e, Z) = {(qe, e)} для всех
 ,
(сокращение магазина).
,
(сокращение магазина).
Автомат сначала переходит в конфигурацию  соответственно определению D' в п.2, затем в
соответственно определению D' в п.2, затем в  ,
,
 соответственно п.1, затем в
соответственно п.1, затем в  соответственно п.3, затем в (qe, e, e) соответственно п.4. Нетрудно показать по индукции, что
соответственно п.3, затем в (qe, e, e) соответственно п.4. Нетрудно показать по индукции, что  (где
(где  ) выполняется для автомата M тогда и только тогда, когда
) выполняется для автомата M тогда и только тогда, когда  выполняется для автомата M'. Поэтому L(M) = L', где L' - язык, допускаемый
автоматом M' опустошением магазина.
выполняется для автомата M'. Поэтому L(M) = L', где L' - язык, допускаемый
автоматом M' опустошением магазина.
Обратно, пусть 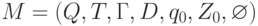 - МП - автомат, допускающий опустошением магазина язык L. Построим
автомат M', допускающий тот же язык по заключительному
состоянию.
- МП - автомат, допускающий опустошением магазина язык L. Построим
автомат M', допускающий тот же язык по заключительному
состоянию.
Пусть  , где D' определяется следующим образом:
, где D' определяется следующим образом:
-
 - переход в "режим M ",
- переход в "режим M ", - Для каждого
 определим
определим  - работа в "режиме M " ,
- работа в "режиме M " , - Для всех
 - переход в
заключительное состояние.
- переход в
заключительное состояние.
Нетрудно показать по индукции, что L = L(M'). Одним из важнейших результатов теории контекстно-свободных языков является доказательство эквивалентности МП-автоматов и КС-грамматик.
Теорема 4.2. Язык является контекстно-свободным тогда и только тогда, когда он допускается МП-авто- матом.
Доказательство. Пусть G = (N, T, P, S) - КС-граммати- ка. Построим МП-автомат, допускающий язык L(G) опустошением магазина.
Пусть  , где D определяется
следующим образом:
, где D определяется
следующим образом:
- Если
 , то
, то  ,
, -
D(q, a, a) = {(q, e)} для всех
 .
.
Фактически, этот МП-автомат в точности моделирует все
возможные выводы в грамматике G. Нетрудно показать по
индукции, что для любой цепочки  вывод S =>+w в грамматике G существует тогда и только тогда, когда
существует последовательность тактов
вывод S =>+w в грамматике G существует тогда и только тогда, когда
существует последовательность тактов  автомата M.
автомата M.
Наоборот, пусть дан  - МП-
автомат, допускающий опустошением магазина язык L.
- МП-
автомат, допускающий опустошением магазина язык L.
Построим грамматику G, порождающую язык L.
Пусть ![G = (\{ [qZr] \mid q, r \in Q, Z \in \Gamma \} \cup \{S\}, T, P, S)](/sites/default/files/tex_cache/7cdf3353d18451428e56d6bcbbf558ff.png) , где P состоит из правил следующего вида:
, где P состоит из правил следующего вида:
-
![S \rightarrow [q_0Z_0q] \in P](/sites/default/files/tex_cache/c6e06eafc6f64817cd231793c4ab131b.png) для всех
для всех 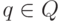 .
. - Если
![(r, e) \in D(q, a, Z), \; \text{то} \; [qZr] \rightarrow a \in P, a \in T \cup \{e\}](/sites/default/files/tex_cache/5dd73d6107b72af9a36f1c223a9d5ad8.png) ,
, - Если
 , то
, то
![\begin{align*}
\text{$[qZs_k] \rightarrow a[rX_1s_1][s_1X_2s_2] \ldots [s_{k-1}X_ks_k]$} \\
\text{для любого набора $s_1, s_2, \ldots , s_k$ состояний из $Q$,}
\end{align*}](/sites/default/files/tex_cache/463c42301c0f7ec86221330ec75da57b.png)
Нетерминалы и правила вывода грамматики определены так, что работе автомата M при обработке цепочки w соответствует левосторонний вывод w в грамматике G.
Индукцией по числу шагов вывода в G или числу тактов M нетрудно показать, что  тогда и только тогда, когда [qAp] =>+ w.
тогда и только тогда, когда [qAp] =>+ w.
Тогда, если  , то S => [q0Z0q] =>+ w для некоторого
, то S => [q0Z0q] =>+ w для некоторого 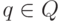 . Следовательно,
. Следовательно,  и поэтому
и поэтому 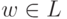 . Аналогично, если
. Аналогично, если 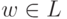 , то
, то  . Значит, S =>[q0Z0q] =>+ w, и поэтому
. Значит, S =>[q0Z0q] =>+ w, и поэтому  .
.
МП-автомат  называется детерминированным (ДМП-автоматом), если выполнены два
следующих условия:
называется детерминированным (ДМП-автоматом), если выполнены два
следующих условия:
(1) Множество D(q, a, Z) содержит не более одного
элемента для любых  ;
;
(2) Если  , то
, то 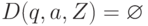 для всех
для всех  .
.
Допускаемый ДМП-автоматом язык называется детерминированным КС-языком.
Так как функция переходов ДМП-автомата содержит не более одного элемента для любой тройки аргументов, мы будем пользоваться записью D(q, a, Z) = (p, u) для обозначения D(q, a, Z) = {(p, u)}.
Пример 4.2. Рассмотрим ДМП-автомат
M = ({q0, q1, q2}, {a, b, c}, {Z, a, b}, D, q0, Z, {q2}),
функция переходов которого определяется следующим образом:
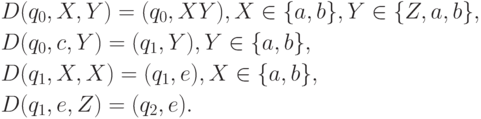
Нетрудно показать, что этот детерминированный МП-автомат
допускает язык  .
.
К сожалению, ДМП-автоматы имеют меньшую распознавательную способность, чем МП-автоматы. Доказано, в частности, что существуют КС-языки, не являющиеся детерминированными КС-языками (таковым, например, является язык из примера 4.1).
Рассмотрим еще один важный вид МП-автомата.
Расширенным автоматом с магазинной памятью назовем
семерку  , где смысл всех
символов тот же, что и для обычного МП-автомата,
кроме D, представляющего собой отображение конечного
подмножества множества
, где смысл всех
символов тот же, что и для обычного МП-автомата,
кроме D, представляющего собой отображение конечного
подмножества множества  во множество
конечных подмножеств множества
во множество
конечных подмножеств множества  . Все остальные
определения (конфигурации, такта, допустимости) для
расширенного МП-автомата остаются такими же, как для
обычного.
. Все остальные
определения (конфигурации, такта, допустимости) для
расширенного МП-автомата остаются такими же, как для
обычного.

