Лексический анализ
Связь регулярных множеств, конечных автоматов и регулярных грамматик
В разделе 3.3.3 приведен алгоритм построения детерминированного конечного автомата по регулярному выражению. Рассмотрим теперь как по описанию конечного автомата построить регулярное множество, совпадающее с языком, допускаемым конечным автоматом.
Теорема 3.1. Язык, допускаемый детерминированным конечным автоматом, является регулярным множеством.
Доказательство. Пусть L - язык, допускаемый детерминированным конечным автоматом
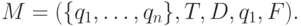
Введем De - расширенную функцию переходов автомата M: De(q, w) = p, где  , тогда и только тогда, когда
, тогда и только тогда, когда 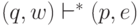 .
.
Обозначим посредством 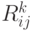 множество всех слов x таких, что De(qi, x) = qj и если De(qi, y) = qs для любой цепочки y
- префикса x, отличного от x и e, то s <= k.
множество всех слов x таких, что De(qi, x) = qj и если De(qi, y) = qs для любой цепочки y
- префикса x, отличного от x и e, то s <= k.
Иными словами, 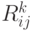 есть множество всех слов, которые
переводят конечный автомат из состояния qi в состояние qj, не проходя ни через какое состояние qs для s > k. Однако, i
и j могут быть больше k.
есть множество всех слов, которые
переводят конечный автомат из состояния qi в состояние qj, не проходя ни через какое состояние qs для s > k. Однако, i
и j могут быть больше k.
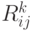 может быть определено рекурсивно следующим
образом:
может быть определено рекурсивно следующим
образом:
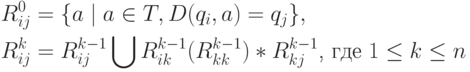
Таким образом, определение 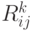 означает, что для входной
цепочки w, переводящей M из qi в qj без перехода через
состояния с номерами, большими k, справедливо ровно одно
из следующих двух утверждений:
означает, что для входной
цепочки w, переводящей M из qi в qj без перехода через
состояния с номерами, большими k, справедливо ровно одно
из следующих двух утверждений:
- Цепочка w принадлежит
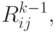 то есть при анализе
цепочки w автомат никогда не достигает состояний с
номерами, большими или равными k.
то есть при анализе
цепочки w автомат никогда не достигает состояний с
номерами, большими или равными k. - Цепочка w может быть представлена как w = w1w2w3,
где
 (подцепочка w1 переводит M сначала в qk ),
(подцепочка w1 переводит M сначала в qk ), 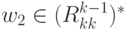 (подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами,
большими или равными k ), и
(подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами,
большими или равными k ), и  (подцепочка w3 переводит M из состояния qk в qj ) -
рис.
3.16.
(подцепочка w3 переводит M из состояния qk в qj ) -
рис.
3.16.
Тогда 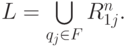 Индукцией по k можно показать, что это множество является регулярным.
Индукцией по k можно показать, что это множество является регулярным.
Таким образом, для всякого регулярного множества имеется конечный автомат, допускающий в точности это регулярное множество, и наоборот - язык, допускаемый конечным автоматом есть регулярное множество.
Рассмотрим теперь соотношение между языками, порождаемыми праволинейными грамматиками и допускаемыми конечными автоматами.
Праволинейная грамматика G = (N, T, P, S) называется регулярной, если
(1) каждое ее правило, кроме S -> e, имеет вид либо A -> aB, либо A -> a, где 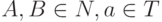 ,
,
(2) в том случае, когда  , начальный символ S не встречается в правых частях правил.
, начальный символ S не встречается в правых частях правил.
Лемма. Пусть G - праволинейная грамматика. Существует регулярная грамматика G' такая, что L(G) = L(G').
Доказательство. Предоставляется читателю в качестве упражнения.
Теорема 3.2. Пусть G = (N, T, P, S) - праволинейная грамматика. Тогда существует конечный автомат M = (Q, T, D, q0, F) для которого L(M) = L(G).
Доказательство. На основании приведенной выше леммы, без ограничения общности можно считать, что G - регулярная грамматика.
Построим НКА M следующим образом:
- состояниями M будут нетерминалы G плюс новое
состояние R, не принадлежащее N. Так что
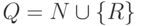 ,
, - в качестве начального состояния M примем S, то есть q0 = S,
- если P содержит правило S -> e, то
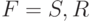 , иначе F = {R}. Напомним, что S не встречается в правых
частях правил, если
, иначе F = {R}. Напомним, что S не встречается в правых
частях правил, если  ,
, - состояние
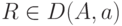 , если
, если 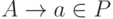 . Кроме того, D(A, a) содержит все B такие, что
. Кроме того, D(A, a) содержит все B такие, что 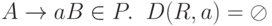 , для каждого
, для каждого  .
.
M, читая вход w, моделирует вывод w в грамматике G. Покажем, что L(M) = L(G). Пусть 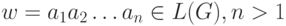 . Тогда
. Тогда 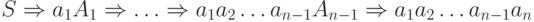 для некоторой последовательности нетерминалов A1, A2, ... , An-1. По определению, D(S, a1)
содержит A1, D(A1, a2) содержит A2, и т.д., D(An-1, an)
содержит R. Так что
для некоторой последовательности нетерминалов A1, A2, ... , An-1. По определению, D(S, a1)
содержит A1, D(A1, a2) содержит A2, и т.д., D(An-1, an)
содержит R. Так что 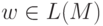 , поскольку De(S, w) содержит R, а
, поскольку De(S, w) содержит R, а 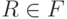 . Если
. Если 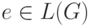 , то
, то 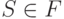 , так что e \in L(M).
, так что e \in L(M).
Аналогично, если  , то существует последовательность состояний S, A1, A2, ... , An-1, R такая, что D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д. Поэтому
, то существует последовательность состояний S, A1, A2, ... , An-1, R такая, что D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д. Поэтому  - вывод в G и
- вывод в G и  . Если
. Если 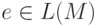 , то
, то 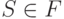 , так что
, так что  и
и 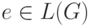 .
.
Теорема 3.3. Для каждого конечного автомата M = (Q, T, D, q0, F) существует праволинейная грамматика G = (N, T, P, S) такая, что L(G) = L(M).
Доказательство. Без потери общности можно считать, что автомат M - детерминированный. Определим грамматику G следующим образом:
- нетерминалами грамматики G будут состояния автомата M. Так что N = Q,
- в качестве начального символа грамматики G примем q0, то есть S = q0,
-
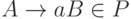 , если D(A, a) = B,
, если D(A, a) = B, -
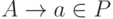 , если D(A, a) = B и
, если D(A, a) = B и 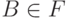 ,
, -
 , если
, если  .
.
Доказательство того, что 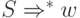 тогда и только тогда,
когда
тогда и только тогда,
когда 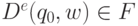 , аналогично доказательству теоремы 3.2.
, аналогично доказательству теоремы 3.2.
В некоторых случаях для определения того, является ли язык регулярным, может быть полезным необходимое условие, которое называется леммой Огдена о разрастании.
Теорема 3.4. (Лемма о разрастании для регулярных
множеств). Пусть L - регулярное множество.
Существует такая константа k, что если 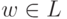 и
и  , то цепочку w можно представить в виде xyz, где
, то цепочку w можно представить в виде xyz, где 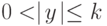 и
и 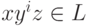 для всех
для всех 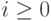 .
.
Доказательство. Пусть 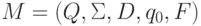 - конечный
автомат, допускающий L, то есть L(M) = L и k = |Q|.
Пусть
- конечный
автомат, допускающий L, то есть L(M) = L и k = |Q|.
Пусть 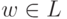 и
и  . Рассмотрим последовательность конфигураций, которые проходит автомат M, допуская
цепочку w. Так как в ней по крайней мере k + 1
конфигурация, то среди первых k+1 конфигурации найдутся
две с одинаковыми состояниями. Таким образом, получаем
существование такой последовательности тактов, что
. Рассмотрим последовательность конфигураций, которые проходит автомат M, допуская
цепочку w. Так как в ней по крайней мере k + 1
конфигурация, то среди первых k+1 конфигурации найдутся
две с одинаковыми состояниями. Таким образом, получаем
существование такой последовательности тактов, что

для некоторых 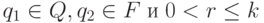 .
Отсюда
.
Отсюда 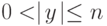 . Но тогда для любого i > 0 автомат может проделать последовательность тактов
. Но тогда для любого i > 0 автомат может проделать последовательность тактов 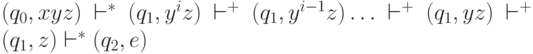 Таким образом,
Таким образом, 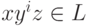 для всех i >= 1. Случай i = 0 то
есть
для всех i >= 1. Случай i = 0 то
есть 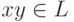 также очевиден.
также очевиден.
С помощью леммы о разрастании можно показать, что не является регулярным множеством язык L={0n1n|n>=1}.
Допустим, что L регулярен. Тогда для достаточно
большого n0n1n можно представить в виде xyz, причем 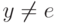 и
и 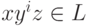 для всех i >= 0. Если
для всех i >= 0. Если  или
или  , то
, то 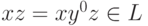 . Если
. Если 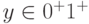 , то
, то 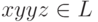 . Получили
противоречие. Следовательно, L не может быть регулярным
множеством.
. Получили
противоречие. Следовательно, L не может быть регулярным
множеством.

