Языки и их представление
Линейно-ограниченные автоматы и их связь с контекстно-зависимыми грамматиками
Каждый КЗ-язык является рекурсивным, но обратное не
верно. Покажем что существует алгоритм, позволяющий для
произвольного КЗ-языка L в алфавите T, и произвольной
цепочки  определить, принадлежит ли w языку L.
определить, принадлежит ли w языку L.
Теорема 2.6. Каждый контекстно-зависимый язык является рекурсивным языком.
Доказательство. Пусть L - контекстно-зависимый язык. Тогда существует некоторая неукорачивающая грамматика G = (N, T, P, S), порождающая L.
Пусть  . Если n = 0, то есть w = e, то
принадлежность
. Если n = 0, то есть w = e, то
принадлежность 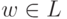 проверяется тривиальным образом.
Так что будем предполагать, что n > 0.
проверяется тривиальным образом.
Так что будем предполагать, что n > 0.
Определим множество Tm как множество строк  длины не более n таких, что вывод
длины не более n таких, что вывод  имеет не более m шагов. Ясно, что T0 = {S}.
имеет не более m шагов. Ясно, что T0 = {S}.
Легко показать, что Tm можно получить из Tm-1 просматривая, какие строки с длиной, меньшей или равной n можно вывести из строк из Tm-1 применением одного правила, то есть

Если  и
и  для некоторого m. Если
из S не выводится u или |u| > n, то u не принадлежит Tm ни
для какого m.
для некоторого m. Если
из S не выводится u или |u| > n, то u не принадлежит Tm ни
для какого m.
Очевидно, что 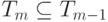 для всех m > 1. Поскольку Tm зависит только от Tm-1, если Tm = Tm-1, то Tm = Tm+1 = Tm+2 = .... Процедура будет вычислять T1, T2, T3, . .. пока для некоторого m не окажется Tm = Tm-1. Если w не
принадлежит Tm, то не принадлежит и L(G), поскольку для j > m выполнено Tj = Tm. Если
для всех m > 1. Поскольку Tm зависит только от Tm-1, если Tm = Tm-1, то Tm = Tm+1 = Tm+2 = .... Процедура будет вычислять T1, T2, T3, . .. пока для некоторого m не окажется Tm = Tm-1. Если w не
принадлежит Tm, то не принадлежит и L(G), поскольку для j > m выполнено Tj = Tm. Если 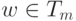 , то
, то 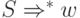 .
.
Покажем, что существует такое m, что Tm = T m-1. Поскольку для каждого i > 1 справедливо 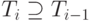 , то если
, то если 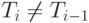 , то число элементов в Ti по крайней мере на 1 больше, чем в Ti-1. Пусть
, то число элементов в Ti по крайней мере на 1 больше, чем в Ti-1. Пусть  . Тогда число строк в
. Тогда число строк в  длины меньшей или равной n равно
длины меньшей или равной n равно  . Только эти строки могут
быть в любом Ti. Значит, Tm = Tm-1 для некоторого
. Только эти строки могут
быть в любом Ti. Значит, Tm = Tm-1 для некоторого 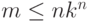 .
Таким образом, процедура, вычисляющая Ti для всех
.
Таким образом, процедура, вычисляющая Ti для всех  до тех пор, пока не будут найдены два равных множества,
гарантированно заканчивается, значит, это алгоритм.
до тех пор, пока не будут найдены два равных множества,
гарантированно заканчивается, значит, это алгоритм.
Линейно-ограниченный автомат (ЛОА) - это
недетерминированная машина Тьюринга с одной лентой,
которая никогда не выходит за пределы |w| ячеек, где w - вход. Формально, линейно-ограниченный автомат
обозначается как  . Обозначения имеют
тот же смысл, что и для машин Тьюринга. Q - это множество
состояний,
. Обозначения имеют
тот же смысл, что и для машин Тьюринга. Q - это множество
состояний, 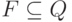 - множество заключительных состояний,
- множество заключительных состояний,  - множество ленточных символов,
- множество ленточных символов, 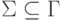 - множество входных символов,
- множество входных символов, 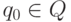 - начальное состояние, D - отображение из
- начальное состояние, D - отображение из  в подмножество
в подмножество  .
.
 содержит два специальных символа, обычно
обозначаемых
содержит два специальных символа, обычно
обозначаемых  и $, - левый и правый концевые маркеры,
соответственно. Эти символы располагаются сначала по
концам входа и их функция - предотвратить переход головки
за пределы области, в которой расположен вход.
и $, - левый и правый концевые маркеры,
соответственно. Эти символы располагаются сначала по
концам входа и их функция - предотвратить переход головки
за пределы области, в которой расположен вход.
Конфигурация M и отношение 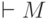 , связывающее две
конфигурации, если вторая может быть получена из
первой применением D, определяются так же, как и
для машин Тьюринга. Конфигурация M обозначается как
, связывающее две
конфигурации, если вторая может быть получена из
первой применением D, определяются так же, как и
для машин Тьюринга. Конфигурация M обозначается как
(q,A1A2,...,An,i) где  -целое
от 1 до n. Предположим, что
-целое
от 1 до n. Предположим, что  и i > 1
и i > 1
Будем говорить, что
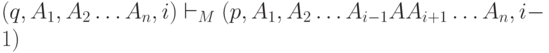
 и i < n, будем говорить, что
и i < n, будем говорить, что
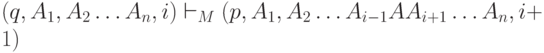
То есть M печатает A поверх Ai, меняет состояние на p
и передвигает головку влево или вправо, но не за пределы
области, в которой символы располагались исходно. Как
обычно, определим отношение  как
как
 и
и
Если  и
и  ,
,
то 
Язык, допускаемый M - это 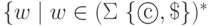 и
и  для некоторого
для некоторого 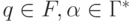 и целого i}.
и целого i}.
Будем называть M детерминированным, если D(q, A)
содержит не более одного элемента для любых  .
Не известно, совпадает ли класс множеств, допускаемых
детерминированными и недетеминированными ЛОА. Ясно,
что любое множество, допускаемое недетерминированным
ЛОА, допускается некоторой детерминированной МТ.
Однако, число ячеек ленты, требуемой этой МТ, может
экспоненциально зависеть от длины входа.
.
Не известно, совпадает ли класс множеств, допускаемых
детерминированными и недетеминированными ЛОА. Ясно,
что любое множество, допускаемое недетерминированным
ЛОА, допускается некоторой детерминированной МТ.
Однако, число ячеек ленты, требуемой этой МТ, может
экспоненциально зависеть от длины входа.
Класс множеств, допускаемых ЛОА, в точности совпадает с классом контекстно - зависимых языков.
Теорема 2.7. Если L - контекстно-зависимый язык, то L допускается ЛОА.
Доказательство. Пусть G = (VN, VT, P, S) - контекстно-
зависимая грамматика. Построим ЛОА M такой, что он
допускает язык L(G). Не вдаваясь в детали построения M, поскольку он довольно сложен, рассмотрим схему его
работы. В качестве ленточных символов будем рассматривать
пары  В начальной конфигурации лента содержит (@, B), (a1, B), ... (an, B), ($, B), где a1 ... an = w - входная цепочка, n=|w|. Цепочку символов
В начальной конфигурации лента содержит (@, B), (a1, B), ... (an, B), ($, B), где a1 ... an = w - входная цепочка, n=|w|. Цепочку символов  n будем называть " первым треком ",
n будем называть " первым треком ",  n - " вторым треком ". Первый трек
будет содержать входную строку x с концевыми маркерами.
Второй трек будет использоваться для вычислений. На
первом шаге M помещает символ S в самой левой ячейке
второго трека. Затем M выполняет процедуру генерации в
соответствии со следующими шагами:
n - " вторым треком ". Первый трек
будет содержать входную строку x с концевыми маркерами.
Второй трек будет использоваться для вычислений. На
первом шаге M помещает символ S в самой левой ячейке
второго трека. Затем M выполняет процедуру генерации в
соответствии со следующими шагами:
- Процедура выбирает подстроку символов
 из второго
трека такую, что
из второго
трека такую, что  .
. - Подстрока
 заменяется на
заменяется на 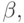 перемещая, если
необходимо, вправо символы справа от
перемещая, если
необходимо, вправо символы справа от  . Если эта
операция могла бы привести к перемещению символа за
правый концевой маркер, ЛОА останавливается.
. Если эта
операция могла бы привести к перемещению символа за
правый концевой маркер, ЛОА останавливается. - Процедура недетерминированно выбирает перейти на шаг 1 или завершиться.
На выходе из процедуры первый трек все еще содержит
строку x, а второй трек содержит строку  такую, что
такую, что 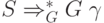 ЛОА сравнивает символы первого трека с
соответствующими символами второго трека. Если сравнение
неуспешно, строки символов первого и второго треков не
одинаковы и ЛОА останавливается без допуска. Если строки
одинаковы, ЛОА останавливается и допускает.
ЛОА сравнивает символы первого трека с
соответствующими символами второго трека. Если сравнение
неуспешно, строки символов первого и второго треков не
одинаковы и ЛОА останавливается без допуска. Если строки
одинаковы, ЛОА останавливается и допускает.
Если 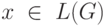 , то существует некоторая
последовательность шагов, на которой ЛОА строит x на
втором треке и допускает вход. Аналогично, для того, чтобы
ЛОА допустил x, должна существовать последовательность
шагов такая, что x может быть построен на втором треке.
Таким образом, должен быть вывод x из S в G.
, то существует некоторая
последовательность шагов, на которой ЛОА строит x на
втором треке и допускает вход. Аналогично, для того, чтобы
ЛОА допустил x, должна существовать последовательность
шагов такая, что x может быть построен на втором треке.
Таким образом, должен быть вывод x из S в G.
Отметим схожесть этих рассуждений и рассуждений в случае произвольной грамматики. Тогда промежуточные сентенциальные формы могли иметь длину, произвольно большую по сравнению с длиной входа. Как следствие, требовалась вся мощь машин Тьюринга. В случае контекстно- зависимых грамматик промежуточные сентенциальные формы не могут быть длиннее входа.
Теорема 2.8. Если L допускается ЛОА, то L - контекстно - зависимый язык.
Доказательство. Конструкция КЗГ по ЛОА аналогична конструкции грамматики типа 0, моделирующей машину Тьюринга. Различие заключатся в том, что нетерминалы КЗГ должны указывать не только текущее и исходное содержимое ячеек ленты ЛОА, но и то, является ли ячейка соседней справа или слева с концевым маркером. Кроме того, состояние ЛОА должно комбинироваться с символом под головкой, поскольку КЗГ не может иметь раздельные символы для концевых маркеров и состояния ЛОА, так как эти символы должны были бы быть заменены на e, когда строка превращается в терминальную.
Теорема 2.9. Существуют рекурсивные множества, не являющиеся контекстно - зависимыми.
Доказательство. Все строки в {0,1}* можно занумеровать. Пусть xi - i -ое слово. Мы можем занумеровать все грамматики типа 0, терминальными символами которых являются 0 и 1. Поскольку имена переменных не важны и каждая грамматика имеет конечное их число, можно предположить, что существует счетное число переменных.
Представим переменные в двоичной кодировке как 01, 011, 0111, 01111 и т.д. Предположим, что 01 всегда является стартовым символом. Кроме того, в этой кодировке терминал 0 будет представляться как 00, а терминал 1 как 001. Символ " -> " представляется как 0011, а запятая как 00111. Любая грамматика с терминалами 0 и 1 может быть представлена строкой правил, использующей стрелку (0011) для разделения левой и правой частей, и запятой (00111) для разделения правил. Строки, представляющие символы, используемые в правилах, - это 00, 001 и 01i для i = 1, 2, ... Множество используемых переменных определяется неявно правилами.
Отметим, что не все строки из 0 и 1 представляют грамматики, и не обязательно КЗГ. Однако, по данной строке легко можно сказать, представляет ли она КЗГ. i - ю грамматику можно найти, генерируя двоичные строки в описанном порядке пока не сгенерируется i -я строка, являющаяся КЗГ. Поскольку имеется бесконечное число КЗГ, их можно занумеровать в некотором порядке G1, G2, ...
Определим 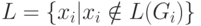 . L рекурсивно. По
строке xi легко можно определить i и затем определить Gi. По теореме 2.6. имеется алгоритм, определяющий для xi принадлежит ли он L(Gi), поскольку Gi КЗГ. Таким
образом имеется алгоритм для определения для любого x
принадлежит ли он G.
. L рекурсивно. По
строке xi легко можно определить i и затем определить Gi. По теореме 2.6. имеется алгоритм, определяющий для xi принадлежит ли он L(Gi), поскольку Gi КЗГ. Таким
образом имеется алгоритм для определения для любого x
принадлежит ли он G.
Покажем теперь, что L не генерируется никакой
КЗ-грамматикой. Предположим, что L генерируется КЗ-
грамматикой Gi. Во-первых, предположим, что  .
Поскольку
.
Поскольку  . Но тогда по определению
. Но тогда по определению  - противоречие. Таким образом предположим,
что
- противоречие. Таким образом предположим,
что 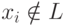 . Поскольку
. Поскольку  . Но тогда
по определению
. Но тогда
по определению 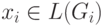 - снова противоречие. Из чего
можно заключить, что L не генерируется Gi. Поскольку
приведенный выше аргумент справедлив для каждой КЗ-
грамматики Gi в перечислении, и поскольку перечисление
содержит все КЗ-грамматики, можно заключить, что L не
КЗ-язык. Поэтому L - рекурсивное множество, не являющееся
контекстно-зависимым.
- снова противоречие. Из чего
можно заключить, что L не генерируется Gi. Поскольку
приведенный выше аргумент справедлив для каждой КЗ-
грамматики Gi в перечислении, и поскольку перечисление
содержит все КЗ-грамматики, можно заключить, что L не
КЗ-язык. Поэтому L - рекурсивное множество, не являющееся
контекстно-зависимым.

