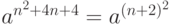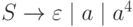Языки и их представление
Теорема 2.1. Каждый контекстно-свободный язык может быть порожден неукорачивающей контекстно- свободной грамматикой.
Доказательство. Пусть L - контекстно-свободный язык. Тогда существует контекстно-свободная грамматика G = (N, T, P, S), порождающая L.
Построим новую грамматику G' = (N',T,P',S') следующим образом:
- Если в P есть правило вида
 , где
, где  для
для  и ни из одной цепочки
и ни из одной цепочки 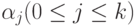 не выводится e, то включить в P' все правила (кроме
не выводится e, то включить в P' все правила (кроме  ) видагде
) видагде
 это либо
это либо  , либо e.
, либо e.
- Если
 , то включить в P' правила
, то включить в P' правила 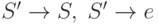 и положить
и положить 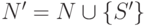 . В противном случае положить
. В противном случае положить  и
и  .
Порождает ли грамматика пустую цепочку можно
установить следующим простым алгоритмом:
.
Порождает ли грамматика пустую цепочку можно
установить следующим простым алгоритмом:Шаг 1. Строим множество

Шаг 2. Строим множество

Шаг 3. Если
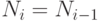 , перейти к шагу 4, иначе шаг 2.
, перейти к шагу 4, иначе шаг 2.Шаг 4. Если
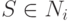 , значит
, значит  .
.Легко видеть, что
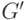 - неукорачивающая грамматика.
Можно показать по индукции, что
- неукорачивающая грамматика.
Можно показать по индукции, что  .
.
Пусть Ki - класс всех языков типа i. Доказано, что
справедливо следующее (строгое) включение: 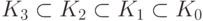 .
.
Заметим, что если язык порождается некоторой грамматикой, это не означает, что он не может быть порожден грамматикой с более сильными ограничениями на правила. Приводимый ниже пример иллюстрирует этот факт.
Пример 2.8. Рассмотрим грамматику  . Эта грамматика является контекстно-свободной. Легко показать, что
. Эта грамматика является контекстно-свободной. Легко показать, что  . Однако, в примере 2.7 приведена
праволинейная грамматика, порождающая тот же язык.
. Однако, в примере 2.7 приведена
праволинейная грамматика, порождающая тот же язык.
Ниже приводятся подробные примеры решения двух практически интересных более сложных задач на построение КС- и НС-грамматик.
Пример 2.9. Данный пример относится к несколько парадоксальной для грамматик постановке: построить КС-грамматику, порождающую язык:
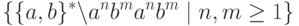
т.е. построить все цепочки кроме указанных (обычно-то говорят о том, что надо построить). Но, может быть, в такой постановке заложена и подсказка к решению? Известно, что иные задачи с подобными требованиями так и решаются: нужно сделать все, "что не надо", а потом отклониться от этого "не надо" всеми возможными способами.
Однако воодушевлнных построением в рамках КС-
грамматики цепочек вида  (здесь и далее в этом
примере
(здесь и далее в этом
примере 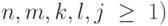 ждет некоторое разочарование.
Действительно, в отличие от таких случаев, как
ждет некоторое разочарование.
Действительно, в отличие от таких случаев, как  ,
,  ,
, 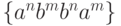 и т.п., обе зависимости (по n и по m )
придется отслеживать одновременно и из двух разных центров
порождения, к чему КС-грамматики по своей природе (виду своих
правил) оказываются не предназначены.
и т.п., обе зависимости (по n и по m )
придется отслеживать одновременно и из двух разных центров
порождения, к чему КС-грамматики по своей природе (виду своих
правил) оказываются не предназначены.
Попробуем тогда пересказать условие задачи в конструктивном (созидательном) плане, т.е. обозначая лишь то, что нам нужно построить, а не наоборот. Поначалу такое множество цепочек кажется необозримым. Но попробуем, "Дорогу осилит идущий"! Начнем с очевидных случаев:
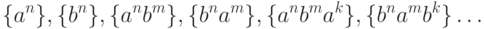
Однако бесконечно продолжать в духе  уже как-
то скучно. Замечаем, что
уже как-
то скучно. Замечаем, что  вполне конечным образом
определяет половину из упомянутых бесчисленных описаний, а в
следующий момент симметрия нам подсказывает и язык
вполне конечным образом
определяет половину из упомянутых бесчисленных описаний, а в
следующий момент симметрия нам подсказывает и язык  .
.
Таким образом, все цепочки вышеперечисленных видов укладываются в три случая:

Далее рассмотрим случай  . Но что такое, к примеру,
. Но что такое, к примеру,  ? То же самое, что объединение условий
? То же самое, что объединение условий 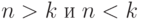 ! И здесь перешли к конструктиву, который несложно строится в рамках КС-грамматики.
! И здесь перешли к конструктиву, который несложно строится в рамках КС-грамматики.
Остается единственный неупомянутый случай:
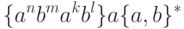
Вспоминая, что объединение КС-языков есть КС-язык, получаем искомое решение задачи.
Так, если язык 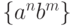 может быть порожден грамматикой
может быть порожден грамматикой

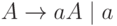
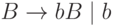
а язык  - грамматикой
- грамматикой


то для объединения этих языков (в общем случае использующих каждый свой уникальный набор вспомогательных знаков) достаточно добавить правило старта из новой общей аксиомы:
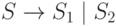
Пример 2.10. Построение НС-грамматики.
Грамматики непосредственных составляющих (или, кратко, НС-грамматики) есть вид представления контекстно-зависимых грамматик, т.е. они обладают теми же выразительными возможностями, что и КЗ-грамматики в целом. Каждое правило НС-грамматики должно соответствовать виду:

то есть левое и правое окружение (контекст) заменяемого знака
A должны сохраниться и вокруг непустой заменяющей цепочки  (греческая буква "эта".
(греческая буква "эта".
Такое дополнительное ограничение позволяет удобнее переходить от КЗ-грамматики к соответствующему линейно- ограниченному автомату
Рассмотрим построение НС-грамматики для языка
 , порождающего слова вида
, порождающего слова вида 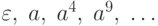
Для большей ясности сперва построим для этого языка грамматику общего вида, а потом перестроим ее в соответствии с НС-ограничениями.
Сам алгоритм порождения  может основываться как на
известном свойстве квадратов чисел, разность между соседними
из которых образуют арифметическую прогрессию, так и на
собственно "квадратности" интересующих чисел, т.е. того, что
каждое квадратное число представимо наподобие матрицы из n
строк и n столбцов единичных элементов (в связи с чем Пифагор
и дал название подобным числам - квадратные, а среди других
чисел по тому же принципу отметил треугольные, кубические,
пирамидальные и т.п.). Последний подход представляется более
общим, поскольку подобным образом мы сможем построить и
может основываться как на
известном свойстве квадратов чисел, разность между соседними
из которых образуют арифметическую прогрессию, так и на
собственно "квадратности" интересующих чисел, т.е. того, что
каждое квадратное число представимо наподобие матрицы из n
строк и n столбцов единичных элементов (в связи с чем Пифагор
и дал название подобным числам - квадратные, а среди других
чисел по тому же принципу отметил треугольные, кубические,
пирамидальные и т.п.). Последний подход представляется более
общим, поскольку подобным образом мы сможем построить и  .
.
Итак, порождаем две группы по n элементов
Получили  но что делать с C и D? Сделав свое дело, они стали лишними.
но что делать с C и D? Сделав свое дело, они стали лишними.
В грамматике общего вида такие знаки сокращают
("увольняют"), а в КЗ-грамматиках - "переводят на другую
работу" (в основные знаки). Но если мы просто напишем 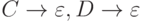 , вывод в случайный момент времени может закончиться
досрочно и станет возможным порождение лишних цепочек.
, вывод в случайный момент времени может закончиться
досрочно и станет возможным порождение лишних цепочек.
Поэтому в обоих случаях не обойтись без дальнейшего уточнения предназначения (миссий) и состава "действующих лиц". Отметим для этого самый первый из команды знаков C (назовем его B ) и самый последний из D (обозначим его E ). Когда B и E встретятся, это и будет признаком полного завершения процесса порождения знаков a.
Начнем вывод с начала:
| Правила | Вид получаемой цепочки |
 |
 |
 |
 |
 |
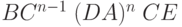 ( C прошло первый раз) ( C прошло первый раз) |
 |
 (прошли все C) (прошли все C) |
 |
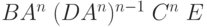 |
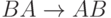 |
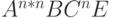 (ушли все D) (ушли все D) |
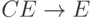 |
 (ушли все C) (ушли все C) |
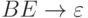 |
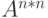 (ушли B c E) (ушли B c E) |
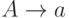 |
 |
Результат получили, но какой ценой (для B, C, D и E )? Прямо-таки сталинские методы. Точнее скажем, в военных или иных чрезвычайных условиях иначе, порой, и нет возможности поступить. А в более мирное время? Попробуем "соблюдать КЗОТ" и обойтись без сокращений.
Снова:


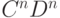
 (A задерживает C)
(A задерживает C)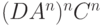 (отработали все C)
(отработали все C)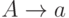
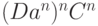
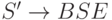
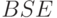
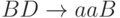

 (ушли все D)
(ушли все D)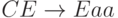
 (ушли все C)
(ушли все C) (ушли B c E)
(ушли B c E)