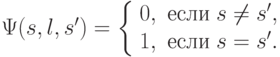|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие алгоритмы
Рассмотрим некоторые случаи выбора множеств, функций, операций,
отношений. Пусть 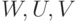 — непустые множества, тогда функцию
— непустые множества, тогда функцию  из
из  в
в  будем называть
будем называть  -функцией
-функцией  из
из  в
в  ;
;  есть степень, с которой
значение функции в точке
есть степень, с которой
значение функции в точке  есть
есть  .
.
 -функция является вероятностной, если для любого
-функция является вероятностной, если для любого 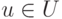 существует
существует  и
и 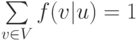 .
.
 -функция является детерминированной, если для любого
-функция является детерминированной, если для любого 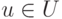 существует
существует 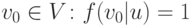 и для
любого
и для
любого 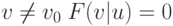 .
.
Если множество  с определенными на нем операциями и
отношениями
записать в виде четверки
с определенными на нем операциями и
отношениями
записать в виде четверки  , то:
, то:
-
![\(
{{W}}_{{X}} = \left\{ {[0,1],{{\max}}{{, \min}}{{, }} \leqslant } \right\}
\)](/sites/default/files/tex_cache/1166e6a1c417bc511799902043f365fd.png) — определяет максиминную машину;
— определяет максиминную машину; -
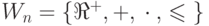 — определяет взвешенную машину;
— определяет взвешенную машину; -
![\(
{{W}}_{{I}} = \left\{ {[0,1],{{\min}}{{, \max}}{{, }} \leqslant } \right\}
\)](/sites/default/files/tex_cache/bdd2501c570c0804bf53ae22cd6975ac.png) — минимаксную машину;
— минимаксную машину; -
![\(
{{W}}_{{T}} = \left\{ {[0,1],{{\max}}{{, }} \cdot {{, }} \leqslant }
\right\}
\)](/sites/default/files/tex_cache/3a0b852d4462a47ef87dc8087aa05f6c.png) — максимально взвешенную машину;
— максимально взвешенную машину; -
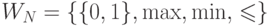 — недетерминированную машину.
— недетерминированную машину.
Взвешенная машина является вероятностной, если функции входа, действий, условий, выхода являются вероятностными. Любая же машина, в которой перечисленные функции являются детерминированными, называется детерминированной.
Рассмотрим программу  , которую допускает
, которую допускает  -машина
-машина  . Для каждой пары
меток
. Для каждой пары
меток 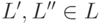 и пары состояний
и пары состояний 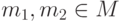 будем
писать
будем
писать  , если в программе
, если в программе  либо имеется инструкция вида
либо имеется инструкция вида 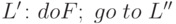 , где
, где 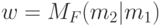 есть степень, с которой осуществляется переход из состояния
есть степень, с которой осуществляется переход из состояния  в состояние
в состояние 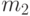 ,
либо имеется инструкция вида
,
либо имеется инструкция вида 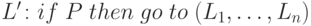 ,
где
,
где 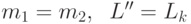 для некоторого
для некоторого 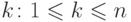 и
и 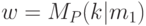 есть степень, с которой осуществляется переход на метку
есть степень, с которой осуществляется переход на метку 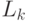 .
.
Выполнением программы  на
на  -машине
-машине  , допускающей
, допускающей  ,
называется конечная последовательность
,
называется конечная последовательность 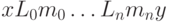 .
Выполнение возможно тогда и только тогда,
если
.
Выполнение возможно тогда и только тогда,
если  ,
где
,
где 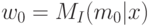 ,
, 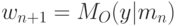 ,
, 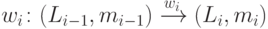 .
.
Таким образом, возможное выполнение определяет последовательность инструкций
программы  , которая может быть реализована на
, которая может быть реализована на  -машине. Таких
последовательностей может быть несколько.
-машине. Таких
последовательностей может быть несколько.
Приведем другую формулировку нечеткой программы, которая является частным случаем данного выше определения нечеткой программы, так как здесь рассматриваются машины с конечным множеством состояний, которые моделируются конечными автоматами.
Для определения нечеткого алгоритма первоначально вводится понятие обобщенной машины, на основе которого формулируется понятие обобщенной нечеткой машины, которое позволяет формализовать понятие нечеткого алгоритма.
Обобщенная машина есть шестерка 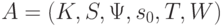 ,
где
,
где  и
и  —
конечные непустые множества машинных инструкций и внутренних состояний
соответственно,
—
конечные непустые множества машинных инструкций и внутренних состояний
соответственно,  — непустое множество с отношением
частичного
порядка
— непустое множество с отношением
частичного
порядка 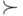 и операциями
и операциями 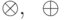 , удовлетворяющими
свойствам коммутативности, ассоциативности и дистрибутивности, а также
содержащие нулевой и единичный элементы;
, удовлетворяющими
свойствам коммутативности, ассоциативности и дистрибутивности, а также
содержащие нулевой и единичный элементы;  —
—  -функция
переходов из состояния в состояние;
-функция
переходов из состояния в состояние; 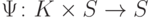 ;
;  и
и  —
начальное состояние и множество финальных состояний.
—
начальное состояние и множество финальных состояний.
Для цепочки инструкций  (
( 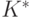 —
множество всевозможных цепочек инструкций) переходов из состояния
—
множество всевозможных цепочек инструкций) переходов из состояния  в
в  определяется
степенью
определяется
степенью 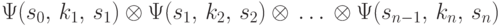 .
.
Если  — пустая цепочка инструкций, то задается расширенная
— пустая цепочка инструкций, то задается расширенная  -функция
-функция  следующим образом:
следующим образом: